Lý thuyết
Định nghĩa
Cho hàm số \[y = f\left( x \right)\] xác định và liên tục trên khoảng \[\left( {a;b} \right)\] và điểm \[{x_0} \in \left( {a;b} \right)\]
+) Nếu tồn tại số \[h > 0\] sao cho \[f\left( x \right) < f\left( {{x_0}} \right)\] với mọi \[x \in \left( {{x_0}–h;{x_0} + h} \right)\] và \[x \ne {x_0}\] thì ta nói hàm số \[y = f\left( x \right)\] đạt cực đại tại \[{x_0}\].
+) Nếu tồn tại số \[h > 0\] sao cho \[f\left( x \right) > f\left( {{x_0}} \right)\] với mọi \[x \in \left( {{x_0}–h;{x_0} + h} \right)\] và \[x \ne {x_0}\] thì ta nói hàm số \[y = f\left( x \right)\] đạt cực tiểu tại \[{x_0}\].
Chú ý:
+) Nếu hàm số \[y = f\left( x \right)\] đạt cực đại tại \[{x_0}\] thì \[{x_0}\] được gọi là điểm cực đại của hàm số;f(\[{x_0}\]) được gọi là giá trị cực đại của hàm số, kí hiệu là \[{f_{C\rlap{–} D}}\] \[\left( {{f_{CT}}} \right)\], còn điểm \[M\left( {{x_0};f\left( {{x_0}} \right)} \right)\] được gọi là điểm cực đại của đồ thị hàm số.
+) Các điểm cực đại và cực tiểu được gọi chung là điểm cực trị. Giá trị cực đại còn gọi là cực đại và được gọi chung là cực trị của hàm số.
Điều kiện cần để hàm số đạt cực trị
Định lí 1:
Giả sử hàm số \[y = f\left( x \right)\] đạt cực trị tại điểm \[{x_0}\]. Khi đó nếu hàm số \[y = f\left( x \right)\] có đạo hàm tại \[{x_0}\] thì \[f’\left( x \right) = 0\]
Điều kiện đủ để hàm số đạt cực trị
Định lí 2:
Giả sử hàm số \[y = f\left( x \right)\] liên tục trên \[K = ({x_0}–h;{x_0} + h)\] và có đạo hàm trên K hoặc trên \[K\backslash \{ {x_0}\} \], với \[h > 0\].
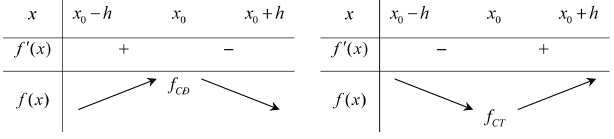
+) Nếu \[f’\left( x \right) > 0\] trên khoảng \[({x_0}–h;{x_0})\] và \[f’\left( x \right) < 0\] trên \[\left( {{x_0};{x_0} + h} \right)\] thì \[{x_0}\] là một điểm cực đại của hàm số \[y = f\left( x \right)\].
+) Nếu \[f’\left( x \right) < 0\] trên khoảng \[({x_0}–h;{x_0})\] và \[f’\left( x \right) > 0\] trên \[\left( {{x_0};{x_0} + h} \right)\] thì \[{x_0}\] là một điểm cực tiểu của hàm số \[y = f\left( x \right)\].
Minh họa bằng bảng biến thiên
Chú ý:
+) Giá trị cực đại f(\[{x_0}\]) của hàm số \[y = f\left( x \right)\] nói chung không phải là giá trị lớn nhất của hàm số \[y = f\left( x \right)\] trên tập xác định của nó.
+) Hàm số chỉ có thể đạt cực trị tại các điểm mà tại đó đạo hàm của hàm số bằng \[0\] hoặc hàm số không có đạo hàm. Ngược lại, đạo hàm có thể bằng \[0\] tại điểm \[{x_0}\] nhưng hàm số không đạt cực trị tại điểm \[{x_0}\].
Định lí 3:
Giả sử hàm số \[y = f\left( x \right)\] có đạo hàm cấp hai trong khoảng \[K = ({x_0}–h;{x_0} + h)\] với \[h > 0\]. Khi đó:
+) Nếu \[f’\left( x \right) = 0\], \[f”\left( {{x_0}} \right) > 0\] thì \[{x_0}\] là điểm cực tiểu.
+) Nếu \[f’\left( x \right) = 0\], \[f”\left( {{x_0}} \right) < 0\] thì \[{x_0}\] là điểm cực đại.
+) Nếu \[f’\left( x \right) = 0\], \[f”\left( {{x_0}} \right) = 0\] thì phải lập bảng biến thiên để kết luận.
Quy tắc tìm cực trị của hàm số
Quy tắc 1
Bước 1: Tìm tập xác định của hàm số.
Bước 2: Tính \[f’\left( x \right)\]. Tìm các điểm tại đó \[f’\left( x \right)\] bằng \[0\] hoặc \[f’\left( x \right)\] không xác định.
Bước 3: Lập bảng biến thiên.
Bước 4: Từ bảng biến thiên suy ra các điểm cực trị.
Quy tắc 2
Bước 1: Tìm tập xác định của hàm số.
Bước 2: Tính \[f’\left( x \right)\]. Giải phương trình \[f’\left( x \right) = 0\] và ký hiệu \[{x_i}\left( {i = 1, 2, 3, …} \right)\] là các nghiệm của nó.
Bước 3: Tính \[f”\left( x \right)\] và \[f”\left( {{x_i}} \right)\]
Bước 4: Dựa vào dấu của \[f”\left( {{x_i}} \right)\] suy ra tính chất cực trị của điểm \[{x_i}\].
Hệ thống bài tập tự luận
Dạng 1. Tìm cực trị của hàm số cho bởi biểu thức.
Câu 1. Tìm cực trị của hàm số \[y = {x^3}–3{x^2}–9x + 1\]
Hướng dẫn giải
TXĐ: \[D = \mathbb{R}\]. Ta có: \[y’ = 3{x^2}–6x–9\]
\[y’ = 0 \Leftrightarrow 3{x^2}–6x–9 \Leftrightarrow \left[ \begin{gathered} x = 3 \hfill \\ x = – 1 \hfill \\ \end{gathered} \right.\]
Cách 1: Bảng biến thiên
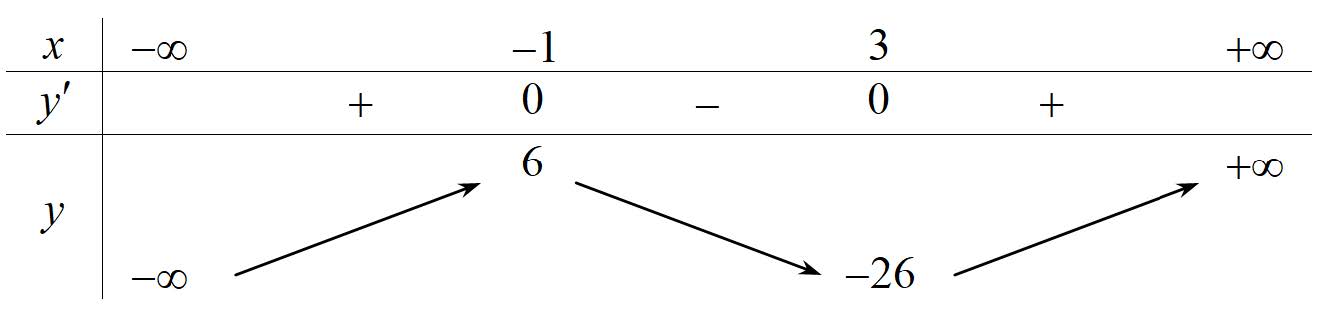
Vậy hàm số đạt cực đại tại \[x = – 1\], \[{y_{C\rlap{–} D}} = 6\] và đạt cực tiểu tại \[x = 3\], \[{y_{CT}} = – 26\]
Cách 2: \[y” = 6x–6\]
\[y”\left( { – 1} \right) = – 12 < 0\] \[ \Rightarrow \] Hàm số đạt cực đại tại \[x = – 1\], \[{y_{C\rlap{–} D}} = 6\]
\[y”\left( 3 \right) = 12 > 0\] \[ \Rightarrow \] Hàm số đạt cực tiểu tại \[x = 3\], \[{y_{CT}} = – 26\]
Câu 2. Tìm cực trị của hàm số \[y = – 2{x^3}–3{x^2}–6x + 1\]
Hướng dẫn giải
TXĐ: \[D = \mathbb{R}\].
Ta có: \[y’ = – 6{x^2} – 6x – 6 = – 6\left[ {{{\left( {x + \frac{1}{2}} \right)}^2} + \frac{3}{4}} \right] < 0,\forall x \in \mathbb{R}\]
Vậy hàm số đã cho không có cực trị
Câu 3. Tìm cực trị của hàm số \[y = {\left( {1–x} \right)^3}{\left( {3x–8} \right)^2}\]
Hướng dẫn giải
TXĐ: \[D = \mathbb{R}\].
Ta có: \[y’ = 15{\left( {1–x} \right)^2}\left( {3x–8} \right)\left( {2–x} \right)\]
\[y’ = 0 \Leftrightarrow \left[ \begin{gathered}
x = \frac{8}{3}\begin{array}{*{20}{c}}
{} \\
{}
\end{array} \hfill \\
x = 1 \hfill \\
x = 2 \hfill \\
\end{gathered} \right.\]
Ta có bảng biến thiên
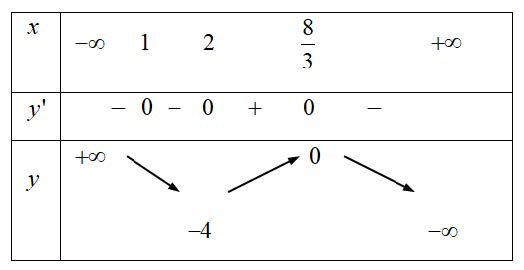
Suy ra hàm số đạt cực đại tại \[x = \frac{8}{3}\], \[{y_{C\rlap{–} D}} = 0\] và hàm số đạt cực tiểu tại \[x = 2\], \[{y_{CT}} = – 4\]
Dạng 2. Riêng về cực trị hàm bậc 3
Cho hàm số bậc ba \[y = f\left( x \right) = a{x^3} + b{x^2} + cx + d\left( {a \ne 0} \right){\text{ }}\left( 1 \right)\]
+) Ta có: \[y’ = 3a{x^2} + 2bx + c\]; \[\Delta’ = {b^2}–3ac\]
- Hàm số không có điểm cực trị \[ \Leftrightarrow \] phương trình \[y’ = 0\] vô nghiệm hoặc có nghiệm kép \[ \Leftrightarrow \] \[\Delta’ \leqslant 0\].
- Hàm số có hai điểm cực trị \[ \Leftrightarrow \] phương trình \[y’ = 0\] có hai nghiệm phân biệt \[ \Leftrightarrow \] \[\Delta’ > 0\].
+) Trong trường hợp \[\Delta’ > 0\] , gọi \[A\left( {{x_1};{y_1}} \right)\], \[B\left( {{x_2};{y_2}} \right)\] là tọa độ hai điểm cực trị của đồ thị hàm số \[\left( 1 \right)\], trong đó \[{x_1}\], \[{x_2}\] là 2 nghiệm phân biệt của phương trình \[y’ = 0\].
Ta có: \[f\left( x \right) = \left( {mx + n} \right) \cdot f’\left( x \right) + r\left( x \right)\], với \[r\left( x \right)\] là nhị thức bậc nhất.
\[ \Rightarrow \left\{ \begin{gathered}
{y_1} = f\left( {{x_1}} \right) = r\left( {{x_1}} \right) \hfill \\
{y_2} = f\left( {{x_2}} \right) = r\left( {{x_2}} \right) \hfill \\
\end{gathered} \right.\]
Suy ra tọa độ \[A\], \[B\] thỏa mãn phương trình \[y = r\left( x \right)\]
Do đó phương trình đường thẳng qua hai điểm cực trị \[A\], \[B\] là \[y = r\left( x \right)\]
Công thức tính nhanh:
Phương trình đường thẳng qua hai điểm cực trị, của đồ thị hàm số \[\left( 1 \right)\] là:
\[y = r\left( x \right) = – \frac{{2\Delta’}}{{9a}}x + \frac{{9ad – bc}}{{9a}}\]
Cách dùng MTCT
+) Nhập biểu thức: \[a{x^3} + b{x^2} + cx + d – \left( {3a{x^2} + 2bx + c} \right)\left( {\frac{x}{3} + \frac{b}{{9a}}} \right)\]
+) Cho \[x = i\] ta được kết quả \[Ai + B\]. Suy ra phương trình đường thẳng đi qua 2 điểm cực trị là \[y = Ax + B\]
Câu 1. Với giá trị nào của tham số \[m\] thì hàm số \[y = \frac{1}{3}{x^3} – m{x^2} + \left( {{m^2} – 4m + 3} \right)x + 2021 – 2020m\] có cực trị?
Hướng dẫn giải
TXĐ: \[D = \mathbb{R}\].
Ta có: \[y’ = {x^2}–2mx + \left( {{m^2}–4m + 3} \right)\]
Hàm số có cực đại, cực tiểu \[ \Leftrightarrow \] \[y’ = 0\] có 2 nghiệm phân biệt \[ \Leftrightarrow \] \[\Delta’ = {m^2}–\left( {{m^2}–4m + 3} \right) > 0\]
\[ \Leftrightarrow \] \[4m–3 > 0\] \[ \Leftrightarrow \] \[m > \frac{3}{4}\]
Vậy \[m > \frac{3}{4}\] thì hàm số có cực đại, cực tiểu
Câu 2. Có bao nhiêu giá trị nguyên của tham số \[m\] để đồ thị hàm số \[y = m{x^3}–\left( {2m–1} \right){x^2} + 2mx–m–1\] có hai điểm cực trị nằm về hai phía của trục hoành?
Hướng dẫn giải
Đồ thị hàm số có hai điểm cực trị nằm về hai phía đối với trục hoành khi và chỉ khi phương trình \[m{x^3}–\left( {2m–1} \right){x^2} + 2mx–m–1\] có 2 nghiệm phân biệt
Ta có: \[m{x^3} – \left( {2m – 1} \right){x^2} + 2mx – m – 1 = 0\]
\[ \Leftrightarrow \left( {x – 1} \right)\left[ {m{x^2} – \left( {m – 1} \right)x + m + 1} \right] = 0\]
\[ \Leftrightarrow \left[ \begin{gathered}
x = 1 \hfill \\
m{x^2} – \left( {m – 1} \right)x + m + 1 = 0{\text{ }}\left( * \right) \hfill \\
\end{gathered} \right.\]
Phương trình có 3 nghiệm phân biệt khi và chỉ khi pt \[\left( * \right)\] có 2 nghiệm phân biệt khác 1
\[ \Leftrightarrow \left\{ \begin{gathered}
m \ne 0 \hfill \\
m – \left( {m – 1} \right) + m + 1 \ne 0 \hfill \\
{\left( {m – 1} \right)^2} – 4m\left( {m + 1} \right) > 0 \hfill \\
\end{gathered} \right.\]
\[ \Leftrightarrow \left\{ \begin{gathered}
m \ne 0 \hfill \\
m + 2 \ne 0 \hfill \\
– 3{m^2} – 6m + 1 > 0 \hfill \\
\end{gathered} \right.\]
\[ \Leftrightarrow \left\{ \begin{gathered}
m \ne 0 \hfill \\
m \ne – 2 \hfill \\
\frac{{ – 3 – 2\sqrt 3 }}{3} < m < \frac{{ – 3 + 2\sqrt 3 }}{3}\begin{array}{*{20}{c}}
{} \\
{}
\end{array} \hfill \\
\end{gathered} \right.\]
Do \[m \in \mathbb{Z}\] \[ \Rightarrow \] \[m = – 1\]
Vậy có 1 giá trị nguyên của tham số thoả mãn đề bài.
Câu 3. Tìm tất cả các giá trị của \[m\] để hàm số \[y = \frac{1}{3}{x^3} – m{x^2} + \left( {m + 2} \right)x\] có cực trị và giá trị của hàm số tại các điểm cực đại, điểm cực tiểu nhận giá trị dương.
Hướng dẫn giải
Cách 1:
Ta có: \[y’ = {x^2} – 2mx + m + 2\]
\[y’ = 0\]\[ \Leftrightarrow \] \[{x^2} – 2mx + m + 2 = 0{\text{ }}\left( 1 \right)\]
Để hàm số có hai cực trị thì phương trình \[\left( 1 \right)\] có hai nghiệm phân biệt
\[\Delta’ > 0 \Leftrightarrow {m^2} – m – 2 > 0 \Leftrightarrow \left[ \begin{gathered}
m < – 1 \hfill \\
m > 2 \hfill \\
\end{gathered} \right.\left( * \right)\]
Phương trình đường thẳng đi qua điểm CĐ, CT của hàm số là
\[y = \left( { – \frac{2}{3}{m^2} + \frac{2}{3}m + \frac{4}{3}} \right)x + \frac{1}{3}m\left( {m + 2} \right)\]
Gọi \[A\left( {{x_1};{y_1}} \right)\], \[B\left( {{x_2};{y_2}} \right)\] là hai điểm cực đại, cực tiểu của đồ thị hàm số, khi đó để hàm số có giá trị cực đại và cực tiểu dương thì \[{y_1} + {y_2} > 0\] và đồ thị hàm số \[y = \frac{1}{3}{x^3} – m{x^2} + \left( {m + 2} \right)x\] cắt trục hoành tại 1 điểm duy nhất
Theo định lý Viet ta có: \[{x_1} + {x_2} = 2m\].
Nên \[{y_1} + {y_2} > 0\]
\[ \Leftrightarrow \left( { – \frac{2}{3}{m^2} + \frac{2}{3}m + \frac{4}{3}} \right)\left( {{x_1} + {x_2}} \right) + \frac{2}{3}m\left( {m + 2} \right) > 0\]
\[ \Leftrightarrow \left( { – \frac{2}{3}{m^2} + \frac{2}{3}m + \frac{4}{3}} \right)\left( {2m} \right) + \frac{2}{3}m\left( {m + 2} \right) > 0\]
\[ \Leftrightarrow 2m\left( { – 2{m^2} + 3m + 6} \right) > 0\]
\[ \Leftrightarrow m \in \left( { – \infty ;\frac{{3 – \sqrt {57} }}{4}} \right) \cup \left( {0;\frac{{3 + \sqrt {57} }}{4}} \right){\text{ }}\left( {**} \right)\]
Để đồ thị hàm số \[y = \frac{1}{3}{x^3} – m{x^2} + \left( {m + 2} \right)x\] cắt trục hoành tại 1 điểm duy nhất thì phương trình \[y = 0\] có 1 nghiệm đơn duy nhất, khi đó \[\frac{1}{3}{x^3} – m{x^2} + \left( {m + 2} \right)x = 0{\text{ }}\left( 2 \right)\] có một nghiệm đơn duy nhất.
Ta có: \[\frac{1}{3}{x^3} – m{x^2} + \left( {m + 2} \right)x = 0\]
\[ \Leftrightarrow x\left( {{x^2} – 3mx + 3m + 6} \right) = 0\]
\[ \Leftrightarrow \left[ \begin{gathered}
x = 0 \hfill \\
{x^2} – 3mx + 3m + 6 = 0{\text{ }}\left( 3 \right) \hfill \\
\end{gathered} \right.\]
Để phương trình \[\left( 1 \right)\] có một nghiệm duy nhất thì phương trình \[\left( 3 \right)\] vô nghiệm, khi đó điều kiện là \[\Delta = 9{m^2} – 12m – 24 < 0\]
\[ \Leftrightarrow \frac{{2 – 2\sqrt 7 }}{3} < m < \frac{{2 + 2\sqrt 7 }}{3}{\text{ }}\left( {***} \right)\]
Kết hợp \[\left( * \right)\], \[\left( {**} \right)\], \[\left( {***} \right)\] ta được tập các giá trị của \[m\] thoả mãn là \[2 < m < \frac{{2 + 2\sqrt 7 }}{3}\]
Cách 2:
Ta có: \[y’ = {x^2} – 2mx + m + 2\]
\[y’ = 0\]\[ \Leftrightarrow \] \[{x^2} – 2mx + m + 2 = 0{\text{ }}\left( 1 \right)\]
Để hàm số có hai cực trị thì phương trình \[\left( 1 \right)\] có hai nghiệm phân biệt, khi đó:
\[\Delta’ > 0 \Leftrightarrow {m^2} – m – 2 > 0 \Leftrightarrow \left[ \begin{gathered}
m < – 1 \hfill \\
m > 2 \hfill \\
\end{gathered} \right.{\text{ }}\left( * \right)\]
Để hàm số có giá trị cực đại, cực tiểu dương thì đồ thị hàm số cắt trục hoành tại 1 điểm duy nhất và giá trị tại điểm uốn luôn dương.
Để hàm số \[y = \frac{1}{3}{x^3} – m{x^2} + \left( {m + 2} \right)x\] cắt trục hoành tại 1 điểm duy nhất thì phương trình \[y = 0\] có 1 nghiệm duy nhất, khi đó \[\frac{1}{3}{x^3} – m{x^2} + \left( {m + 2} \right)x = 0{\text{ }}\left( 2 \right)\] có một nghiệm đơn duy nhất.
Ta có: \[\frac{1}{3}{x^3} – m{x^2} + \left( {m + 2} \right)x = 0\]
\[ \Leftrightarrow x\left( {{x^2} – 3mx + 3m + 6} \right) = 0\]
\[ \Leftrightarrow \left[ \begin{gathered}
x = 0 \hfill \\
{x^2} – 3mx + 3m + 6 = 0{\text{ }}\left( 3 \right) \hfill \\
\end{gathered} \right.\]
Để phương trình \[\left( 1 \right)\] có một nghiệm duy nhất thì phương trình \[\left( 3 \right)\] vô nghiệm, khi đó điều kiện là \[\Delta = 9{m^2} – 12m – 24 < 0\]
\[ \Leftrightarrow \frac{{2 – 2\sqrt 7 }}{3} < m < \frac{{2 + 2\sqrt 7 }}{3}{\text{ }}\left( {**} \right)\]
Để giá trị tại điểm uốn luôn dương:
\[{y’ = {x^2} – 2mx + m + 2}\]
\[{y” = 2x – 2m}\]
\[{y” = 0 \Leftrightarrow 2x – 2m = 0 \Leftrightarrow x = m}\]
Ta có: \[{y_{\left( m \right)}} > 0 \Rightarrow \frac{{{m^3}}}{3} – {m^3} + m\left( {m + 2} \right) > 0\]
\[ \Leftrightarrow m\left( { – 2{m^2} + 3m + 6} \right) > 0\]
\[ \Leftrightarrow m \in \left( { – \infty ;\frac{{3 – \sqrt {57} }}{4}} \right) \cup \left( {0;\frac{{3 + \sqrt {57} }}{4}} \right){\text{ }}\left( {***} \right)\]
Kết hợp \[\left( * \right)\], \[\left( {**} \right)\], \[\left( {***} \right)\] ta được tập các giá trị của \[m\] thoả mãn là \[2 < m < \frac{{2 + 2\sqrt 7 }}{3}\]
Câu 4. Có bao nhiêu giá trị nguyên của tham số \[m\] để đồ thị hàm số \[y = {x^3} – \left( {m + 1} \right){x^2} + \left( {{m^2} – 2} \right)x – {m^2} + 3\] có hai điểm cực trị và hai điểm cực trị đó nằm về cùng một phía đối với trục hoành?
Hướng dẫn giải
TXĐ: \[D = \mathbb{R}\]
\[y’ = 3{x^2} – 2\left( {m + 1} \right)x + {m^2} – 2\] có \[\Delta’ = – 2{m^2} + 2m + 7\]
Để đồ thị hàm số \[y = {x^3} – \left( {m + 1} \right){x^2} + \left( {{m^2} – 2} \right)x – {m^2} + 3\] có hai cực trị thì \[{y’}\] đổi dấu hai lần, tức là \[{y’}\] có hai nghiệm phân biệt, tương đương
\[\Delta’ > 0 \Leftrightarrow – 2{m^2} + 2m + 7 > 0 \Leftrightarrow \frac{{1 – \sqrt {15} }}{2} < m < \frac{{1 + \sqrt {15} }}{2}\]
Vì \[m \in \mathbb{Z}\] nên được \[m \in \left\{ { – 1;0;1;2} \right\}\]
Lúc này hai nghiệm \[{x_1}\];\[{x_2}\] của \[{y’}\] lần lượt là hoành độ các điểm cực trị của hàm số.
Hai điểm cực trị đó nằm cùng 1 phía đối với trục hoành khi và chỉ khi \[f\left( {{x_1}} \right) \cdot f\left( {{x_2}} \right) > 0\], tương đương đồ thị hàm số đã cho cắt trục hoành tại đúng một điểm, tức là, phương trình \[{x^3} – \left( {m + 1} \right){x^2} + \left( {{m^2} – 2} \right)x – {m^3} = 0\] có duy nhất một nghiệm thực.
Xét \[m = – 1\] thì phương trình là \[{x^3} – x + 2 = 0\]: phương trình này có đúng một nghiệm thực nên chọn \[m = – 1\]
Xét \[m = 0\] thì phương trình là \[{x^3} – {x^2} – 2x + 3 = 0\]: phương trình này có đúng một nghiệm thực nên chọn \[m = 0\]
Xét \[m = 1\] thì phương trình là \[{x^3} – 2{x^2} – x + 2 = 0\]: phương trình này có ba nghiệm thực phân biệt nên loại \[m = 1\]
Xét \[m = 2\] thì phương trình là \[{x^3} – 3{x^2} + 2x – 1 = 0\]: phương trình này có đúng một nghiệm thực nên chọn \[m = 2\]
Vậy \[m \in \left\{ { – 1;0;2} \right\}\]
Câu 5. Cho hàm số \[y = {x^3} – 6mx + 4\] có đồ thị \[\left( {{C_m}} \right)\]. Tìm tất cả các giá trị của tham số \[m\] để đường thẳng đi qua điểm cực đại, điểm cực tiểu của đồ thị \[\left( {{C_m}} \right)\] cắt đường tròn tâm \[I\left( {1;0} \right)\], bán kính \[\sqrt 2 \] tại hai điểm phân biệt \[A\]; \[B\] sao cho tam giác \[IAB\] có diện tích lớn nhất.
Hướng dẫn giải
Xét hàm số \[y = {x^3} – 6mx + 4\] có tập xác định \[\mathbb{R}\].
\[y’ = 3{x^2} – 6m\]; \[y’ = 0 \Leftrightarrow {x^2} = 2m\]
Đồ thị hàm số có 2 điểm cực trị \[ \Leftrightarrow \] \[{y’}\] đổi dấu 2 lần
\[ \Leftrightarrow \] \[y’ = 0\] có hai nghiệm phân biệt \[ \Leftrightarrow \] \[m > 0\]
Ta có: \[y = \frac{1}{3}y’x – 4mx + 4\]
Gọi \[M\left( {{x_1};{y_1}} \right)\], \[N\left( {{x_2};{y_2}} \right)\] là hai điểm cực trị của đồ thị hàm số.
Ta có: \[\left\{ \begin{gathered}
y’\left( {{x_1}} \right) = y’\left( {{x_2}} \right) = 0 \hfill \\
{y_1} = y\left( {{x_1}} \right) = \frac{1}{3}y’\left( {{x_1}} \right){x_1} – 4m{x_1} + 4 \hfill \\
{y_2} = y\left( {{x_2}} \right) = \frac{1}{3}y’\left( {{x_2}} \right){x_2} – 4m{x_2} + 4 \hfill \\
\end{gathered} \right.\]
\[ \Rightarrow \left\{ \begin{gathered}
{y_1} = – 4m{x_1} + 4 \hfill \\
{y_2} = – 4m{x_2} + 4 \hfill \\
\end{gathered} \right.\]
Suy ra \[M\], \[N\] thuộc đường thẳng \[d\] có phương trình \[y = – 4mx + 4\]
Vậy phương trình đường thẳng qua hai điểm cực trị của \[\left( {{C_m}} \right)\] là \[y = – 4mx + 4\]
Gọi \[\left( T \right)\] là đường tròn có tâm \[I\left( {1;0} \right)\] và bán kính \[R = \sqrt 2 \]
Đường thẳng \[d\] cắt đường tròn tại hai điểm phân biệt \[A\], \[B\] và tạo thành tam giác \[IAB\]
\[ \Leftrightarrow 0 < d\left( {I;d} \right) < R\]
\[ \Leftrightarrow 0 < d\left( {I;d} \right) < \sqrt 2 \]
\[ \Leftrightarrow \left\{ \begin{gathered}
m \ne 1 \hfill \\
\frac{{\left| { – 4m + 4} \right|}}{{\sqrt {16{m^2} + 1} }} < \sqrt 2 \hfill \\
\end{gathered} \right.\]
Cách 1:
Do đường thẳng \[d\] luôn đi qua điểm \[K\left( {0;4} \right)\],\[IK = \sqrt {17} > R\] \[ \Rightarrow \] \[K\] nằm ngoài đường tròn nên tồn tại hai điểm \[A\], \[B\] là giao điểm của \[d\] với đường tròn để tam giác \[IAB\] vuông tại \[I\].
Do đó: \[{S_{IAB}} = \frac{1}{2}IA \cdot IB \cdot \sin \widehat {AIB} \leqslant \frac{1}{2}IA \cdot IB\]
Dấu “=” xảy ra \[ \Leftrightarrow IA \bot IB\]
\[ \Leftrightarrow d\left( {I;d} \right) = \frac{R}{{\sqrt 2 }} = 1 \Leftrightarrow \frac{{\left| { – 4m + 4} \right|}}{{\sqrt {16{m^2} + 1} }} = 1 \Leftrightarrow m = \frac{{15}}{{32}}\]
Bình luận: Nếu đường thẳng \[d\] luôn đi qua điểm \[K\] cố định mà \[IK < \frac{R}{{\sqrt 2 }}\] thì sẽ không có vị trí của đường thẳng \[d\] để tam giác \[IAB\] vuông tại \[I\]. Khi đó, nếu làm như trên sẽ bị sai. Trong trường hợp đón thì ta phải đặt \[d\left( {I;d} \right) = t\] \[\left( {0 < t \leqslant l} \right)\], với \[l\] là độ dài đoạn thẳng \[IK\], rồi tính \[{S_{\Delta IAB}}f\left( t \right)\] và tìm giá trị lớn nhất của \[f\left( t \right)\] trên nửa khoảng \[\left( {0;l} \right]\].
Cách 2:
Phương trình đường tròn là: \[{\left( {x – 1} \right)^2} + {y^2} = 2{\text{ }}\left( C \right)\]
Xét hệ \[\left\{ \begin{gathered}
{\left( {x – 1} \right)^2} + {y^2} = 2 \hfill \\
y = – 4mx + 4 \hfill \\
\end{gathered} \right.\]
\[ \Rightarrow \left\{ {{{\left( {16{m^2} + 1} \right)}^2} – 2\left( {16m + 1} \right)x + 15 = 0{\text{ }}\left( 1 \right)} \right.\]
\[d\] cắt \[\left( C \right)\] tại 2 điểm phân biệt \[A\], \[B\] \[ \Leftrightarrow \] \[\left( 1 \right)\] có 2 nghiệm phân biệt \[a\], \[b\]
\[ \Leftrightarrow {\left( {16m + 1} \right)^2} – 15\left( {16m + 1} \right) > 0\]
Khi đó: \[A\left( {a; – 4ma + 4} \right)\], \[B\left( {b; – 4mb + 4} \right)\] \[ \Rightarrow \left[ \begin{gathered}
\overrightarrow {IA} = \left( {a – 1; – 4ma + 4} \right) \hfill \\
\overrightarrow {IB} = \left( {b – 1; – 4mb + 4} \right) \hfill \\
\end{gathered} \right.\]
\[\overrightarrow {IA} \cdot \overrightarrow {IB} = ab – \left( {a + b} \right) + 16\left[ {{m^2}a – m\left( {a + b} \right) + 1} \right] + 1 = 0\]
\[ \Leftrightarrow ab – \left( {a + b} \right) + 16{m^2}ab – 16m\left( {a + b} \right) + 17 = 0\]
\[ \Leftrightarrow \left( {16{m^2} + 1} \right)ab – \left( {16m + 1} \right)\left( {a + b} \right) + 17 = 0\]
\[ \Leftrightarrow 15 – \frac{{2{{\left( {16m + 1} \right)}^2}}}{{16{m^2} + 1}} + 17 = 0\]
\[ \Leftrightarrow \frac{{{{\left( {16m + 1} \right)}^2}}}{{16{m^2} + 1}} = 16\]
\[ \Leftrightarrow m = \frac{{15}}{{32}}\]
Dạng 3. Riêng về cực trị hàm trùng phương
Kiến thức cần nhớ
Cho hàm số: \[y = a{x^4} + b{x^2} + c\] \[\left( {a \ne 0} \right)\] có đồ thị là \[\left( C \right)\].
+) Đồ thị \[\left( C \right)\] có đúng một điểm cực trị khi \[y’ = 0\] có đúng một nghiệm \[ \Leftrightarrow \] \[ab \geqslant 0\]
+) Đồ thị \[\left( C \right)\] có ba điểm cực trị khi \[y’ = 0\] có 3 nghiệm phân biệt\[ \Leftrightarrow \] \[ab < 0\]
Khi đó ba điểm cực trị là: \[A\left( {0;c} \right)\], \[B\left( { – \sqrt { – \frac{b}{{2a}}} ; – \frac{\Delta }{{4a}}} \right)\], \[C\left( {\sqrt { – \frac{b}{{2a}}} ; – \frac{\Delta }{{4a}}} \right)\] với \[\Delta = {b^2} – 4ac\]
Độ dài các đoạn thẳng: \[AB = AC = \sqrt {\frac{{{b^4}}}{{16{a^2}}} – \frac{b}{{2a}}} \], \[BC = 2\sqrt { – \frac{b}{{2a}}} \] và tam giác \[{\text{ABC}}\] luôn là tam giác cân tại \[A\].
Công thức nhanh một số trường hợp thường gặp
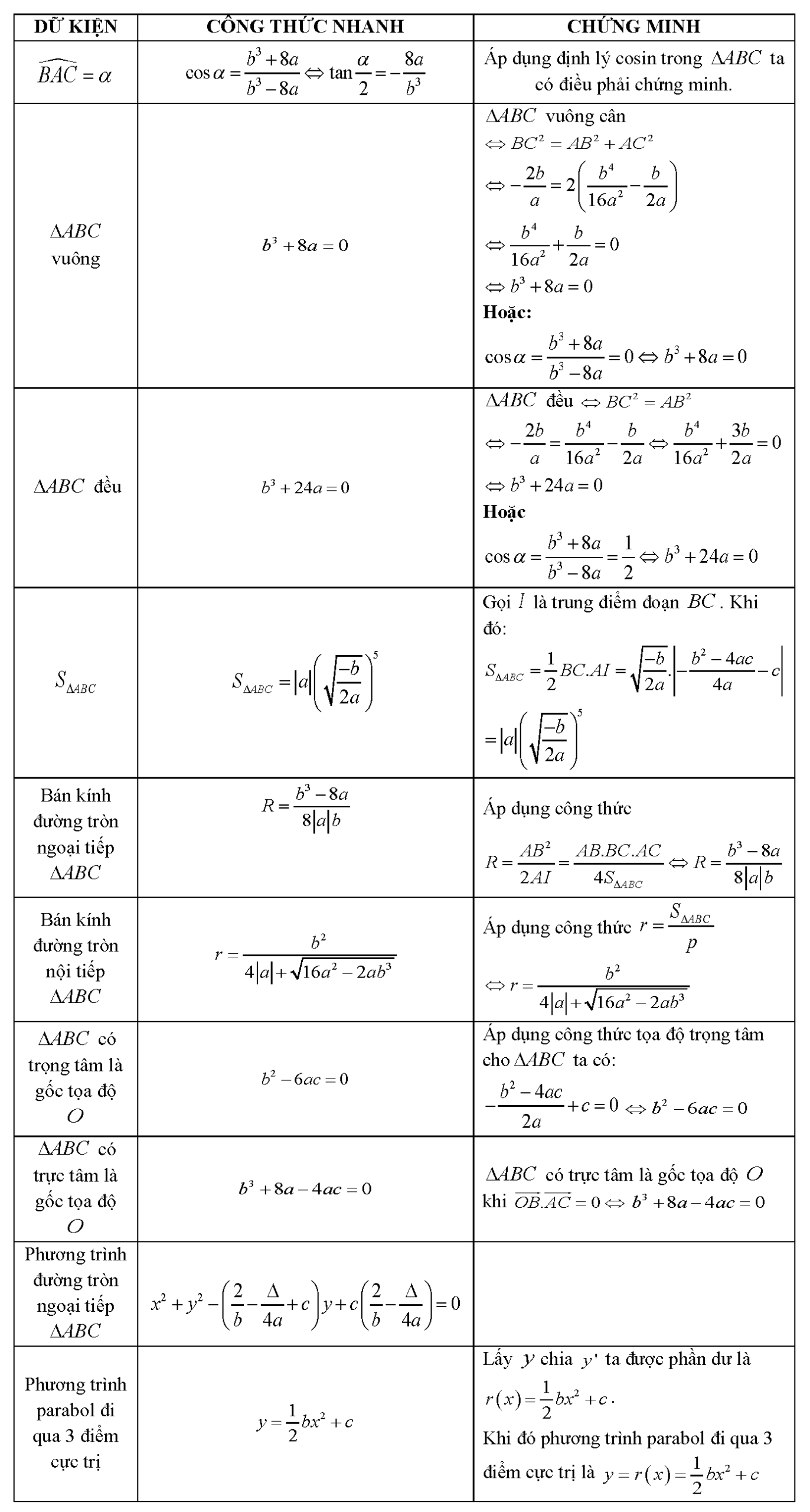
Câu 1. Tìm tất cả các giá trị của tham số \[m\] để hàm số \[y = 2{x^4} – \left( {m + 1} \right){x^2} + 4\] có ba điểm cực trị.
Hướng dẫn giải
Cách 1:
Ta có: \[y’ = 8{x^3} – 2\left( {m + 1} \right)x\]
\[y’ = 0 \Leftrightarrow \left[ \begin{gathered}
x = 0 \hfill \\
x = \frac{{m + 1}}{4}{\text{ }}\left( 1 \right)\begin{array}{*{20}{c}}
{} \\
{}
\end{array} \hfill \\
\end{gathered} \right.\]
Hàm số có ba điểm cực trị khi và chỉ khi \[y’ = 0\] có ba nghiệm phân biệt
\[ \Leftrightarrow \] \[\left( 1 \right)\] có hai nghiệm phân biệt khác \[0\]
\[ \Leftrightarrow \frac{{m + 1}}{4} > 0 \Leftrightarrow m > – 1\]
Cách 2: Hàm số đã cho có 3 cực trị khi và chỉ khi \[ab < 0 \Leftrightarrow m + 1 > 0 \Leftrightarrow m > – 1\]
Câu 2. Cho hàm số \[y = {x^4} – 2\left( {m + 1} \right){x^2} + {m^2}\]. Tìm tất cả các giá trị thực của tham số \[m\] để đồ thị của
hàm số có ba điểm cực trị tạo thành ba đỉnh của một tam giác vuông cân.
Hướng dẫn giải
Cách 1:
TXĐ: \[D = \mathbb{R}\]
Ta có: \[y’ = 4{x^3} – 4\left( {m + 1} \right)x\]
\[y’ = 0 \Leftrightarrow 4{x^3} – 4\left( {m + 1} \right)x = 0 \Leftrightarrow \left[ \begin{gathered}
x = 0 \hfill \\
{x^2} = m + 1 \hfill \\
\end{gathered} \right.\]
Đồ thị hàm số có ba điểm cực trị thì phương trình \[y’ = 0\] có ba nghiệm phân biệt \[ \Leftrightarrow \] \[m > – 1{\text{ }}\left( * \right)\]
Khi đó, ba điểm cực trị là: \[A\left( {0;{m^2}} \right)\], \[B\left( {\sqrt {m + 1} ; – 2m – 1} \right)\], \[C\left( { – \sqrt {m + 1} ; – 2m – 1} \right)\]
Ta thấy \[A \in Oy\], \[B\], \[C\] đối xứng nhau qua \[Oy\] nên tam giác \[{\text{ABC}}\] cân tại \[A\].
Do đó tam giác \[{\text{ABC}}\] vuông cân tại A khi và chỉ khi tam giác \[{\text{ABC}}\] vuông tại \[A\] \[ \Leftrightarrow \overrightarrow {AB} \cdot \overrightarrow {AC} = 0\]
\[\overrightarrow {AB} = \left( {\sqrt {m + 1} ; – {{\left( {m + 1} \right)}^2}} \right)\], \[\overrightarrow {AC} = \left( { – \sqrt {m + 1} ; – {{\left( {m + 1} \right)}^2}} \right)\]
Suy ra: \[\overrightarrow {AB} \cdot \overrightarrow {AC} = 0\]
\[ \Leftrightarrow {\left( {m + 1} \right)^4} – \left( {m + 1} \right) = 0 \Leftrightarrow \left[ \begin{gathered}
m = – 1{\text{ }}\left( {lo\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle\cdot}$}}{a} i} \right) \hfill \\
m = 0{\text{ }}\left( {TM} \right) \hfill \\
\end{gathered} \right.\]
Vậy \[m = 0\] là giá trị cần tìm
Chú ý có thể sử dụng điều kiện sau:
Gọi \[H\] là trung điểm của đoạn thẳng \[BC\] thì \[H\left( {0; – 2m – 1} \right)\]
Khi đó ba điểm cực trị lập thành tam giác vuông cân khi \[{b^3} + 8a = 0 \Leftrightarrow – 8{\left( {m + 1} \right)^3} + 8 = 0 \Leftrightarrow m = 0\]
Câu 3. Cho hàm số \[y = {x^4} – 2m{x^2} + m – 1\], với \[m\] là tham số thực. Xác định các giá trị của tham số \[m\] để đồ thị hàm số có ba cực trị đồng thời các điểm cực trị tạo thành một tam giác có bán kính đường tròn ngoại tiếp bằng 1.
Hướng dẫn giải
TXĐ: \[D = \mathbb{R}\]
Ta có: \[y’ = 4{x^3} – 4mx\]
\[y’ = 0 \Leftrightarrow 4{x^3} – 4mx = 0 \Leftrightarrow 4x\left( {{x^2} – m} \right) = 0 \Leftrightarrow \left[ \begin{gathered}
x = 0 \hfill \\
{x^2} = m \hfill \\
\end{gathered} \right.\]
Hàm số có ba điểm cực trị \[ \Leftrightarrow \] phương trình \[y’ = 0\] có ba nghiệm phân biệt và \[{y’}\] đổi dấu qua các nghiệm đó \[ \Leftrightarrow \] \[m > 0\]
Khi đó ba điểm cực trị của đồ thị hàm số là:
\[A\left( {0;m – 1} \right)\], \[B\left( { – \sqrt m ; – {m^2} + m – 1} \right)\], \[C\left( {\sqrt m ; – {m^2} + m – 1} \right)\]
Cách 1: Ta có: \[{S_{\Delta ABC}} = \frac{1}{2}\left| {{y_B} – {y_A}} \right| \cdot \left| {{x_C} – {x_B}} \right| = {m^2}\sqrt m \] và \[AB = \sqrt {{m^2} + m} \], \[BC = 2\sqrt m \]
Suy ra bán kính đường tròn ngoại tiếp:
\[R = \frac{{AB \cdot AC \cdot BC}}{{4{S_{\Delta ABC}}}} = \frac{{\left( {{m^2} + m} \right) \cdot 2\sqrt m }}{{4{m^2}\sqrt m }}\]
\[R = 1 \Leftrightarrow \frac{{\left( {{m^2} + m} \right) \cdot \sqrt m }}{{2{m^2}\sqrt m }} = 1 \Leftrightarrow \frac{{m + 1}}{{2m}} = 1\]
Cách 2: Gọi \[M\], \[H\] lần lượt là trung điểm của \[AB\], \[BC\] và \[I\] là tâm đường tròn ngoại tiếp \[\Delta ABC\]
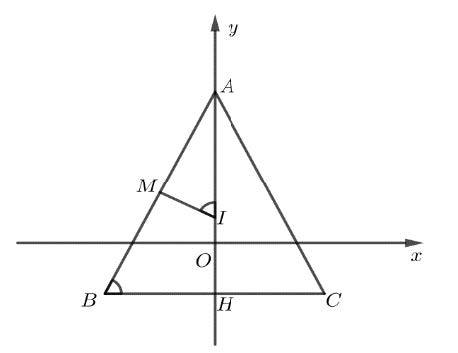
\[AB = \sqrt {{m^2} + m} \], \[AH = {m^2}\]
Ta có: \[\Delta AMI \sim \Delta AHB\]
\[ \Rightarrow R = \frac{{A{B^2}}}{{2AH}}\]
\[R = 1 \Leftrightarrow \frac{{A{B^2}}}{{2AH}} = 1 \Leftrightarrow \frac{{{m^2} + m}}{{2{m^2}}} = 1 \Leftrightarrow \frac{{m + 1}}{{2m}} = 1 \Leftrightarrow m = 1\]
Vậy \[m = 1\]
Câu 4. Cho hàm số \[y = {x^4} – 2m{x^2} + m\], với \[m\] là tham số thực. Tìm tất cả các giá trị của tham số \[m\] để đồ thị hàm số đã cho có 3 điểm cực trị và đường tròn đi qua 3 điểm cực trị này có bán kính bằng 1.
Hướng dẫn giải
TXĐ: \[D = \mathbb{R}\]
\[y’ = 4{x^3} – 4mx = 4x\left( {{x^2} – m} \right)\]
Hàm số có 3 điểm cực trị khi \[y’ = 0\] có 3 nghiệm phân biệt \[ \Leftrightarrow \] \[m > 0\]
Khi đó: \[y’ = 0 \Leftrightarrow \left[ \begin{gathered}
x = 0 \hfill \\
x = \pm \sqrt m \hfill \\
\end{gathered} \right.\]
Khi đó toạ độ ba điểm cực trị: \[A\left( {0;m} \right)\], \[B\left( { – \sqrt m ; – {m^2} + m} \right)\], \[C\left( {\sqrt m ; – {m^2} + m} \right)\]
Gọi \[H\] là trung điểm của cạnh \[BC\]. Ta có: \[H\left( {0; – {m^2} + m} \right)\]
\[{S_{\Delta ABC}} = \frac{1}{2}AH \cdot BC = \frac{{AB \cdot AC \cdot BC}}{{4R}} \Leftrightarrow A{B^2} = 2AH \cdot R\] trong đó \[\left\{ \begin{gathered}
AH = {m^2} \hfill \\
AB = \sqrt {m + {m^4}} \hfill \\
\end{gathered} \right.\]
Suy ra: \[m + {m^4} = 2{m^2}\]
\[ \Leftrightarrow m\left( {{m^3} – 2m + 1} \right) = 0\]
\[ \Leftrightarrow m\left( {m + 1} \right)\left( {{m^2} + m – 1} \right) = 0\]
\[ \Leftrightarrow \left[ \begin{gathered}
m = 0 \hfill \\
m = 1 \hfill \\
m = \frac{{ – 1 + \sqrt 5 }}{2}\begin{array}{*{20}{c}}
{} \\
{}
\end{array} \hfill \\
m = \frac{{ – 1 – \sqrt 5 }}{2}\begin{array}{*{20}{c}}
{} \\
{}
\end{array} \hfill \\
\end{gathered} \right.\]
Đối chiếu điều kiện ta được \[S = \left\{ {1;\frac{{ – 1 + \sqrt 5 }}{2}} \right\}\]
Dạng 4. Cực trị của hàm \[y = \left| {f\left( x \right)} \right|\], \[y = f\left( {\left| x \right|} \right)\]
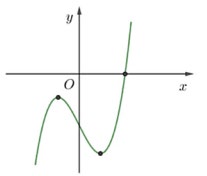
Câu 1. Cho hàm số \[y = f\left( x \right)\] liên tục trên \[\mathbb{R}\] có đồ thị như hình vẽ. Tìm số điểm cực trị của hàm số \[y = f\left( x \right)\].
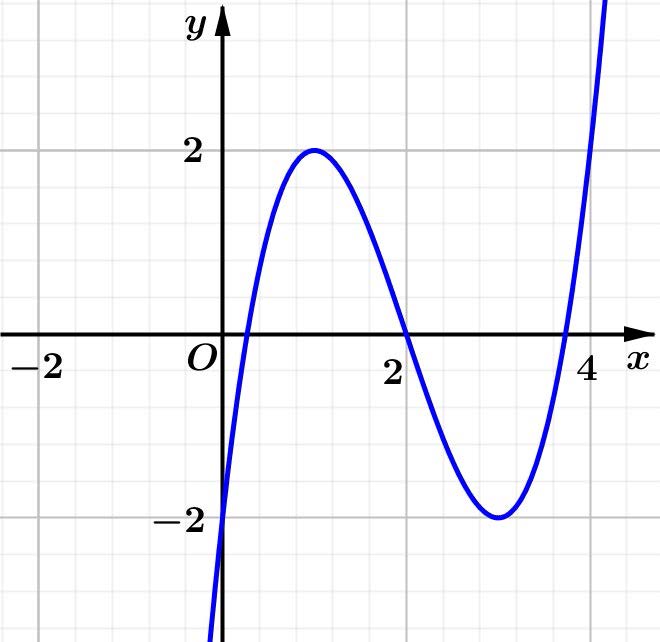
Hướng dẫn giải
Ta có: \[\left| {f\left( x \right)} \right| = \left\{ \begin{gathered}
f\left( x \right){\text{ }}khi{\text{ }}f\left( x \right) \geqslant 0 \hfill \\
– f\left( x \right){\text{ }}khi{\text{ }}f\left( x \right) < 0 \hfill \\
\end{gathered} \right.\]
Do đó đồ thị hàm số \[y = \left| {f\left( x \right)} \right|\] như sau:
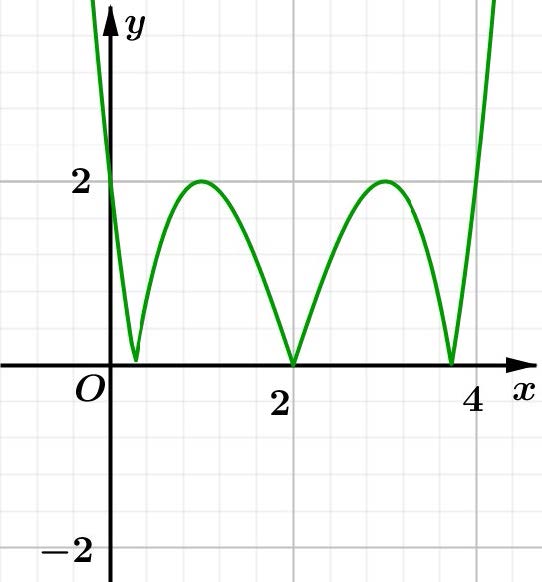
Từ đồ thị suy ra hàm số \[y = \left| {f\left( x \right)} \right|\] có 5 điểm cực trị
Công thức tính nhanh: Số điểm cực trị của hàm số \[y = \left| {f\left( x \right)} \right|\] bằng tổng số điểm cực trị của hàm số \[y = \left| {f\left( x \right)} \right|\] và số lần đổi dấu của hàm số \[f\left( x \right)\]
Câu 2. Cho hàm số \[y = f\left( x \right)\] có bảng biến thiên như sau :
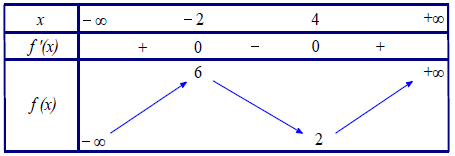
Hàm số \[y = f\left( {\left| {x – 3} \right|} \right)\] có bao nhiêu điểm cực trị?
Hướng dẫn giải
Xét hàm số \[y = g\left( x \right) = f\left( {\left| {x – 3} \right|} \right)\]
Ta có: \[g’\left( x \right) = {\left[ {f\left( {\left| {x – 3} \right|} \right)} \right]^\prime } = {\left( {\left| {x – 3} \right|} \right)^\prime }.f’\left( {\left| {x – 3} \right|} \right) = \frac{{x – 3}}{{\left| {x – 3} \right|}} \cdot f’\left( {\left| {x – 3} \right|} \right)\]
Có \[g’\left( x \right)\] không xác định tại \[x = 3\]
\[g’\left( x \right) = 0 \Leftrightarrow f’\left( {\left| {x – 3} \right|} \right) = 0 \Leftrightarrow \left[ \begin{gathered}
\left| {x – 3} \right| = – 2 \hfill \\
\left| {x – 3} \right| = 4 \hfill \\
\end{gathered} \right. \Leftrightarrow \left[ \begin{gathered}
x = 7 \hfill \\
x = – 1 \hfill \\
\end{gathered} \right.\]
Bảng biến thiên
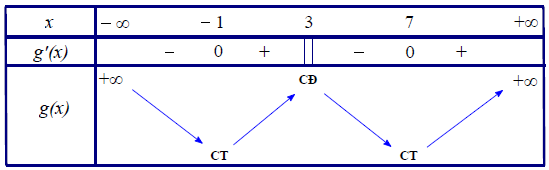
Dựa vào BBT ta thấy hàm số \[y = f\left( {\left| {x – 3} \right|} \right)\] có 3 điểm cực trị.
Câu 3. Cho hàm số \[y = f\left( x \right) = {x^3} – \left( {2m – 1} \right){x^2} + \left( {2 – m} \right)x + 2\]. Tập tất cả các giá trị của \[m\] để đồ thị hàm số \[y = f\left( {\left| x \right|} \right)\] có 5 điểm cực trị là \[\left( {\frac{a}{b};c} \right)\] với \[a\], \[b\], \[c\] là các số nguyên và \[{\frac{a}{b}}\] là phân số tối giản. Tính \[a + b + c\].
Hướng dẫn giải
TXĐ: \[D = \mathbb{R}\]
Ta có: \[f’\left( x \right) = 3{x^2} – 2\left( {2m – 1} \right)x + \left( {2 – m} \right)\]
Đồ thị hàm số \[y = f\left( {\left| x \right|} \right)\] có 5 điểm cực trị
\[ \Leftrightarrow y = f\left( x \right) = {x^3} – \left( {2m – 1} \right){x^2} + \left( {2 – m} \right)x + 2\] có 2 điểm cực trị cùng nằm bên phải trục tung
\[ \Leftrightarrow f’\left( x \right) = 0\] có 2 nghiệm dương phân biệt
\[ \Leftrightarrow \left\{ \begin{gathered}
\Delta ‘ > 0 \hfill \\
S > 0 \hfill \\
P > 0 \hfill \\
\end{gathered} \right. \Leftrightarrow \left\{ \begin{gathered}
{\left( {2m – 1} \right)^2} – 3\left( {2 – m} \right) > 0 \hfill \\
2m – 1 > 0 \hfill \\
2 – m > 0 \hfill \\
\end{gathered} \right.\]
\[ \Leftrightarrow \left\{ \begin{gathered}
4{m^2} – m – 5 > 0 \hfill \\
\frac{1}{2} < m < 2\begin{array}{*{20}{c}}
{} \\
{}
\end{array} \hfill \\
\end{gathered} \right.\]
\[ \Leftrightarrow \left\{ \begin{gathered}
\left[ \begin{gathered}
m < – 1 \hfill \\
m > \frac{5}{4}\begin{array}{*{20}{c}}
{} \\
{}
\end{array} \hfill \\
\end{gathered} \right. \hfill \\
\frac{1}{2} < m < 2\begin{array}{*{20}{c}}
{} \\
{}
\end{array} \hfill \\
\end{gathered} \right.\]
\[ \Leftrightarrow \frac{5}{4} < m < 2\]
\[ \Rightarrow \left( {\frac{a}{b};c} \right) = \left( {\frac{5}{4};2} \right) \Rightarrow a = 5,b = 4,c = 2\]
Vậy \[a + b + c = 11\]