Lý thuyết
Luỹ thừa với số mũ nguyên
+) Luỹ thừa với số mũ nguyên dương: Cho \[a \in \mathbb{R},n \in {\mathbb{N}^*}\]. Khi đó:
\[{a^n} = a \cdot a \ldots a\] (\[n\] thừa số \[a\])
+) Luỹ thừa với số mũ nguyên âm, luỹ thừa với số mũ \[0\]: Cho \[a \ne 0\]. Khi đó:
\[{a^{ – n}} = \frac{1}{{{a^n}}};{\text{ }}{a^0} = 1\]
Chú ý:
+) Luỹ thừa với số mũ nguyên có các tính chất tương tự tính chất của luỹ thừa với số mũ nguyên dương.
+) \[{0^0}\] và \[{0^{ – n}}\] không có nghĩa.
Căn bậc n
Cho \[b \in \mathbb{R},n \in {\mathbb{N}^*}\left( {n \geqslant 2} \right)\]. Số \[a\] được gọi là căn bậc \[n\] của số \[b\] nếu \[{a^n} = b\]
+) Với \[n\] lẻ, \[b \in \mathbb{R}\]: Phương trình \[{x^n} = b\] có duy nhất một căn bậc \[n\] của \[b\], ký hiệu là \[\sqrt[n]{b}\]
+) Với \[n\] chẵn và:
- \[b < 0\]: Không tồn tại căn bậc \[n\] của \[b\]
- \[b = 0\]: Có một căn bậc \[n\] của \[b\] là \[\sqrt[n]{0} = 0\]
- \[b > 0\]: Có hai căn bậc \[n\] của \[b\], kí hiệu là \[\sqrt[n]{b}\] và \[ – \sqrt[n]{b}\]
Tính chất
Với \[a,b \geqslant 0;m,n \in {\mathbb{N}^*};p \in \mathbb{Z}\], ta có:
- \[\sqrt[n]{{ab}} = \sqrt[n]{a} \cdot \sqrt[n]{b}\]
- \[\sqrt[n]{{\frac{a}{b}}} = \frac{{\sqrt[n]{a}}}{{\sqrt[n]{b}}},{\text{ }}b > 0\]
- \[\sqrt[n]{{{a^p}}} = {\left( {\sqrt[n]{a}} \right)^p},{\text{ }}a > 0\]
- \[\sqrt[n]{{\sqrt[m]{a}}} = \sqrt[{n \cdot m}]{a}\]
- \[\sqrt[n]{{{a^n}}} = a\] khi \[n\] lẻ và \[\sqrt[n]{{{a^n}}} = \left| a \right|\] khi \[n\] chẵn
Luỹ thừa với số mũ hữu tỉ
Cho số thực \[a > 0\] và số hữu tỉ \[r = \frac{m}{n}\], trong đó \[m \in \mathbb{Z},n \in {\mathbb{N}^*}\]. Khi đó, luỹ thừa của \[a\] với số mũ \[r\] là số \[{a^r}\] xác định bởi:
\[{a^r} = {a^{\frac{m}{n}}} = \sqrt[n]{{{a^m}}}\]
+) Nếu \[\frac{m}{n} = \frac{{m’}}{{n’}}\] thì \[{a^{\frac{m}{n}}} = {a^{\frac{{m’}}{{n’}}}}\]. Do đó trong biểu thức \[{a^r}\], với \[r\] là một số hữu tỉ, ta thường viết \[r\] dưới dạng phân số tối giản có mẫu số dương.
+) \[{a^{\frac{1}{n}}} = \sqrt[n]{a}\left( {a > 0,n \in {\mathbb{N}^*}} \right)\]
Luỹ thừa với số mũ vô tỉ
+) Mọi số vô tỉ \[\alpha \], bao giờ cũng tồn tại một dãy số hữu tỉ \[\left( {{r_n}} \right)\] để \[\mathop {\lim }\limits_{n \to + \infty } {r_n} = \alpha \]
+) Cho \[a\] là một số thực dương và \[\alpha \] là một số vô tỉ. Xét dãy số hữu tỉ \[\left( {{r_n}} \right)\] mà \[\mathop {\lim }\limits_{n \to + \infty } {r_n} = \alpha \]. Khi đó: \[{a^\alpha } = \mathop {\lim }\limits_{n \to + \infty } {a^{{r_n}}}\]
Lưu ý:
+) \[{a^\alpha }\] với số mũ \[\alpha \] nguyên dương thì cơ số \[a\] có điều kiện \[a \in \mathbb{R}\]
+) \[{a^\alpha }\] với số mũ \[\alpha = 0\] hoặc \[\alpha \] nguyên âm thì cơ số \[a\] có điều kiện \[a \ne 0\]
+) \[{a^\alpha }\] với số mũ \[\alpha \] không nguyên thì cơ số \[a\] có điều kiện \[a > 0\]
Luỹ thừa với số mũ thực
Tính chất
Với mọi \[a,b\] là các số thực dương; \[\alpha ,\beta \] là các số thực tuỳ ý ta có:
- \[{a^\alpha } \cdot {a^\beta } = {a^{\alpha + \beta }}\]
- \[\frac{{{a^\alpha }}}{{{a^\beta }}} = {a^{\alpha – \beta }}\]
- \[{\left( {{a^\alpha }} \right)^\beta } = {\left( {{a^\beta }} \right)^\alpha } = {a^{\alpha \cdot \beta }}\]
- \[{\left( {a \cdot b} \right)^\alpha } = {a^\alpha } \cdot {b^\alpha }\]
- \[{\left( {\frac{a}{b}} \right)^\alpha } = \frac{{{a^\alpha }}}{{{b^\alpha }}}\]
- \[\sqrt[\alpha ]{{a \cdot b}} = \sqrt[\alpha ]{a} \cdot \sqrt[\alpha ]{b}\]
- \[\sqrt[\alpha ]{{\frac{a}{b}}} = \frac{{\sqrt[\alpha ]{a}}}{{\sqrt[\alpha ]{b}}}\]
- \[\sqrt[\alpha ]{{\sqrt[\beta ]{a}}} = \sqrt[{\alpha \cdot \beta }]{a}\]
- \[\sqrt[\alpha ]{{{a^\beta }}} = {\left( {\sqrt[\alpha ]{a}} \right)^\beta } = {a^{\frac{\beta }{\alpha }}}\]
So sánh hai luỹ thừa
So sánh cùng cơ số
+) Nếu cơ số \[a > 1\] thì \[\alpha > \beta \Leftrightarrow {a^\alpha } > {a^\beta }\]
+) Nếu cơ số \[0 < a < 1\] thì \[\alpha > \beta \Leftrightarrow {a^\alpha } < {a^\beta }\]
So sánh cùng số mũ
+) Nếu số mũ \[\alpha > 0\] thì \[a > b > 0 \Rightarrow {a^\alpha } > {b^\alpha }\]
+) Nếu số mũ \[\alpha < 0\] thì \[a > b > 0 \Rightarrow {a^\alpha } < {b^\alpha }\]
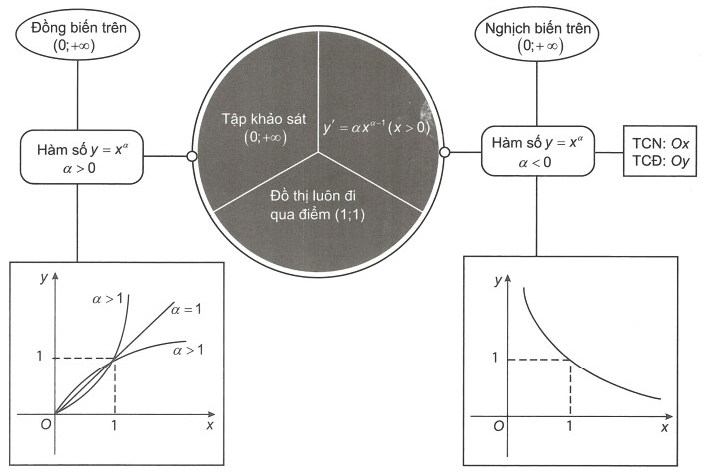
Sơ đồ hệ thống hoá luỹ thừa
Bài tập tự luyện
Dạng 1. Tính toán
Câu 1. Tính giá trị của biểu thức \[{\left( {{5^{ – \frac{2}{3}}}} \right)^{ – 3}} + {\left( {{{\left( {0,2} \right)}^{\frac{3}{5}}}} \right)^{ – 5}}\]
Hướng dẫn giải
Ta có: \[{\left( {{5^{ – \frac{2}{3}}}} \right)^{ – 3}} + {\left( {{{\left( {0,2} \right)}^{\frac{3}{5}}}} \right)^{ – 5}} = {5^2} + {\left( {0,2} \right)^{ – 3}} = {5^2} + {5^3} = 150\]
Câu 2. Tính giá trị của biểu thức \[\sqrt[3]{{\frac{2}{5} \cdot \sqrt[7]{{\frac{2}{5} \cdot \sqrt[3]{{\frac{2}{5}}}}}}} \cdot \left( {\frac{2}{5}} \right)\]
Hướng dẫn giải
Ta có: \[\sqrt[3]{{\frac{2}{5} \cdot \sqrt[7]{{\frac{2}{5} \cdot \sqrt[3]{{\frac{2}{5}}}}}}} \cdot \left( {\frac{2}{5}} \right)\]\[ = \sqrt[3]{{\frac{2}{5} \cdot \sqrt[7]{{\frac{2}{5} \cdot {{\left( {\frac{2}{5}} \right)}^{\frac{1}{3}}}}}}} \cdot \left( {\frac{2}{5}} \right)\]\[ = \sqrt[3]{{\frac{2}{5} \cdot \sqrt[7]{{{{\left( {\frac{2}{5}} \right)}^{\frac{4}{3}}}}}}} \cdot \left( {\frac{2}{5}} \right)\]\[ = \sqrt[3]{{\frac{2}{5} \cdot {{\left( {\frac{2}{5}} \right)}^{\frac{4}{{21}}}}}} \cdot \left( {\frac{2}{5}} \right)\]\[ = {\left( {\frac{2}{5}} \right)^{\frac{{25}}{{63}}}} \cdot \left( {\frac{2}{5}} \right) = {\left( {\frac{2}{5}} \right)^{\frac{{88}}{{63}}}}\]
Câu 3. Cho \[a,b\] là 2 số thực khác \[0\]. Biết \[{\left( {\frac{1}{{125}}} \right)^{{a^2} + 4ab}} = {\left( {\sqrt[3]{{625}}} \right)^{3{a^2} – 10ab}}\]. Tính tỉ số \[\frac{a}{b}\].
Hướng dẫn giải
Ta có: \[{\left( {\frac{1}{{125}}} \right)^{{a^2} + 4ab}} = {\left( {\sqrt[3]{{625}}} \right)^{3{a^2} – 10ab}}\]
\[ \Leftrightarrow {5^{ – 3\left( {{a^2} + 4ab} \right)}} = {5^{\frac{4}{3}\left( {3{a^2} – 10ab} \right)}}\]
\[ \Leftrightarrow – 3{a^2} – 12ab = 4{a^2} – \frac{{40}}{3}ab\]
\[ \Leftrightarrow 7{a^2} – \frac{4}{3}ab = 0\]
\[ \Leftrightarrow 7a – \frac{4}{3}b = 0{\text{ }}\left( {do{\text{ }}a \ne 0} \right)\]
\[ \Leftrightarrow \frac{a}{b} = \frac{4}{{21}}\]
Vậy \[\frac{a}{b} = \frac{4}{{21}}\]
Câu 4. Tích \[\left( {2017} \right)!{\left( {1 + \frac{1}{1}} \right)^1}{\left( {1 + \frac{1}{2}} \right)^2} \ldots {\left( {1 + \frac{1}{{2017}}} \right)^{2017}}\] được viết dưới dạng \[{a^b}\], khi đó \[\left( {a;b} \right)\] là bộ số nào?
Hướng dẫn giải
Ta có: \[\left( {2017} \right)!{\left( {1 + \frac{1}{1}} \right)^1}{\left( {1 + \frac{1}{2}} \right)^2} \ldots {\left( {1 + \frac{1}{{2017}}} \right)^{2017}}\]
\[ = \left( {2017} \right)!{\left( {\frac{2}{1}} \right)^1}{\left( {\frac{3}{2}} \right)^2} \ldots {\left( {\frac{{2017}}{{2016}}} \right)^{2016}}{\left( {\frac{{2018}}{{2017}}} \right)^{2017}}\]
\[ = \left( {2017} \right)!\frac{1}{1} \cdot \frac{1}{2} \cdot \frac{1}{3} \ldots \frac{1}{{2016}} \cdot \frac{{{{2018}^{2017}}}}{{2017}} = {2018^{2017}}\]
\[ \Rightarrow a = 2018;b = 2017\]
Vậy \[\left( {a;b} \right) = \left( {2018;2017} \right)\]
Câu 5. Cho biểu thức \[f\left( x \right) = \frac{1}{{{{2018}^x} + \sqrt {2018} }}\]. Tính tổng sau:
\[S = \sqrt {2018} \left[ {f\left( { – 2017} \right) + f\left( { – 2016} \right) + \ldots + f\left( 0 \right) + f\left( 1 \right) + \ldots + f\left( {2018} \right)} \right]\]
Hướng dẫn giải
Ta có: \[f\left( {1 – x} \right) = \frac{1}{{{{2018}^{1 – x}} + \sqrt {2018} }}\]\[ = \frac{{{{2018}^x}}}{{2018 + {{2018}^x}\sqrt {2018} }}\]\[ = \frac{{{{2018}^x}}}{{\sqrt {2018} \left( {{{2018}^x} + \sqrt {2018} } \right)}}\]
\[ \Rightarrow f\left( x \right) + f\left( {1 – x} \right)\]\[ = \frac{1}{{{{2018}^x} + \sqrt {2018} }} + \frac{{{{2018}^x}}}{{\sqrt {2018} \left( {{{2018}^x} + \sqrt {2018} } \right)}}\]\[ = \frac{1}{{\sqrt {2018} }}\]
Do \[1 – 2018 = – 2017\] nên \[f\left( { – 2017} \right) + f\left( {2018} \right) = \frac{1}{{\sqrt {2018} }}\]
\[f\left( { – 2016} \right) + f\left( {2017} \right) = \frac{1}{{\sqrt {2018} }},\]
\[ \cdots \cdots \cdots \]
\[f\left( 0 \right) + f\left( 1 \right) = \frac{1}{{\sqrt {2018} }}.\]
\[ \Rightarrow f\left( { – 2017} \right) + f\left( { – 2016} \right) + \ldots + f\left( 0 \right) + f\left( 1 \right) + \ldots + f\left( {2018} \right)\]
\[ = \frac{1}{{\sqrt {2018} }} + \frac{1}{{\sqrt {2018} }} + \ldots + \frac{1}{{\sqrt {2018} }}\] (\[{2018}\] thừa số)
\[ = 2018 \cdot \frac{1}{{\sqrt {2018} }} = \sqrt {2018} \]
Vậy \[S = 2018\]
Câu 6. Có tất cả bao nhiêu bộ ba số thực \[\left( {x;y;z} \right)\] thoả mãn đồng thời các điều kiện dưới đây
\[{2^{\sqrt[3]{{{x^2}}}}} \cdot {4^{\sqrt[3]{{{y^2}}}}} \cdot {16^{\sqrt[3]{{{z^2}}}}} = 128\] và \[{\left( {x{y^2} + {z^4}} \right)^2} = 4 + {\left( {x{y^2} – {z^4}} \right)^2}\]
Hướng dẫn giải
+) \[{2^{\sqrt[3]{{{x^2}}}}} \cdot {4^{\sqrt[3]{{{y^2}}}}} \cdot {16^{\sqrt[3]{{{z^2}}}}} = 128\]
\[ \Leftrightarrow {2^{\sqrt[3]{{{x^2}}} + 2\sqrt[3]{{{y^2}}} + 4\sqrt[3]{{{z^2}}}}} = {2^7}\]
\[ \Leftrightarrow \sqrt[3]{{{x^2}}} + 2\sqrt[3]{{{y^2}}} + 4\sqrt[3]{{{z^2}}} = 7{\text{ }}\left( 1 \right)\]
+) \[{\left( {x{y^2} + {z^4}} \right)^2} = 4 + {\left( {x{y^2} – {z^4}} \right)^2}\]
\[ \Leftrightarrow x{y^2}{z^4} = 1\]
\[ \Leftrightarrow \sqrt[3]{x} \cdot \sqrt[3]{{{y^2}}} \cdot \sqrt[3]{{{z^4}}} = 1\] và \[x > 0{\text{ }}\left( 2 \right)\]
Đặt \[a = \sqrt[3]{x} > 0\] (theo \[\left( 2 \right)\]), \[b = \sqrt[3]{y}\], \[c = \sqrt[3]{z}\]\[ \Rightarrow a{b^2}{c^4} = 1\]
Theo bất đẳng thức AM-GM, ta có:
\[7 = {a^2} + 2{b^2} + 4{c^2} = {a^2} + {b^2} + {b^2} + {c^2} + {c^2} + {c^2} + {c^2} \geqslant 7\sqrt[7]{{{a^2}{b^4}{c^8}}} = 7\]
Dấu “\[ = \]” xảy ra khi và chỉ khi \[{a^2} = {b^2} = {c^2}\] hay \[\sqrt[3]{{{x^2}}} = \sqrt[3]{{{y^2}}} = \sqrt[3]{{{z^2}}}\]
Thay vào \[\left( 1 \right)\] ta được \[\sqrt[3]{{{x^2}}} = \sqrt[3]{{{y^2}}} = \sqrt[3]{{{z^2}}} = 1\]. Vì \[x > 0\] nên có 4 bộ số thoả mãn là: \[\left( {x;y;z} \right) = \left( {1;1;1} \right)\], \[\left( {x;y;z} \right) = \left( {1; – 1;1} \right)\], \[\left( {x;y;z} \right) = \left( {1;1; – 1} \right)\], \[\left( {x;y;z} \right) = \left( {1; – 1; – 1} \right)\].
Dạng 2. So sánh các luỹ thừa
Câu 1. So sánh các số
a\ \[{\left( {\sqrt 2 – 1} \right)^{2019}}\] và \[{\left( {\sqrt 2 – 1} \right)^{2020}}\]
b\ \[{\pi ^{1015}}\] và \[3,{14^{1015}}\]
Hướng dẫn giải
a\ Vì \[0 < \sqrt 2 – 1 < 1\] và \[2019 < 2020\] nên \[{\left( {\sqrt 2 – 1} \right)^{2019}} > {\left( {\sqrt 2 – 1} \right)^{2020}}\]
b\ Vì \[1015 > 0\] và \[\pi > 3,14\] nên \[{\pi ^{1015}} > 3,{14^{1015}}\]
Câu 2. So sánh các số
a\ \[\sqrt[3]{{15}}\] và \[\sqrt[4]{{20}}\]
b\ \[\sqrt[3]{7} + \sqrt {15} \] và \[\sqrt {10} + \sqrt[3]{{28}}\]
Hướng dẫn giải
a\ Vì \[\sqrt[3]{{15}} = \sqrt[{12}]{{{{15}^4}}} = \sqrt[{12}]{{50625}}\] và \[\sqrt[4]{{20}} = \sqrt[{12}]{{{{20}^3}}} = \sqrt[{12}]{{8000}}\]
Mà \[50625 > 8000\] nên \[\sqrt[3]{{15}} > \sqrt[4]{{20}}\]
b\ Vì \[\sqrt[3]{7} + \sqrt {15} < \sqrt[3]{8} + \sqrt {16} = 2 + 4 = 6\] và \[\sqrt {10} + \sqrt[3]{{28}} > \sqrt 9 + \sqrt[3]{{27}} = 3 + 3 = 6\]
Vậy \[\sqrt[3]{7} + \sqrt {15} < \sqrt {10} + \sqrt[3]{{28}}\]
Câu 3. Có thể kết luận gì về số \[a\] nếu:
a\ \[{\left( {2 – a} \right)^{\frac{3}{4}}} > {\left( {2 – a} \right)^2}\]
b\ \[{\left( {1 – a} \right)^{ – \frac{1}{3}}} > {\left( {1 – a} \right)^{ – \frac{1}{2}}}\]
Hướng dẫn giải
a\ Ta có: \[\frac{3}{4} < 2\] mà \[{\left( {2 – a} \right)^{\frac{3}{4}}} > {\left( {2 – a} \right)^2}\] nên \[0 < 2 – a < 1 \Leftrightarrow 1 < a < 2\]
b\ Ta có: \[ – \frac{1}{3} > – \frac{1}{2}\] mà \[{\left( {1 – a} \right)^{ – \frac{1}{3}}} > {\left( {1 – a} \right)^{ – \frac{1}{2}}}\] nên \[1 – a > 1 \Leftrightarrow a < 0\]
Câu 4. Cho \[U = 2 \cdot {2019^{2020}}\], \[V = {2019^{2020}}\], \[W = 2018 \cdot {2019^{2019}}\], \[X = 5 \cdot {2019^{2019}}\] và \[Y = {2019^{2019}}\]. Trong các số sau đây, số nào bé nhất \[X – Y;U – V;V – W;W – X\]?
Hướng dẫn giải
\[{X – Y = 5 \cdot {{2019}^{2019}} – {{2019}^{2019}} = 4 \cdot {{2019}^{2019}}}\]
\[{U – V = 2 \cdot {{2019}^{2020}} – {{2019}^{2020}} = {{2019}^{2020}} = 2019 \cdot {{2019}^{2019}}}\]
\[{V – W = 2019 \cdot {{2019}^{2019}} – 2018 \cdot {{2019}^{2019}} = {{2019}^{2019}}}\]
\[{W – X = 2018 \cdot {{2019}^{2019}} – 5 \cdot {{2019}^{2019}} = 2013 \cdot {{2019}^{2019}}}\]
Vậy trong các số trên, số nhỏ nhất là \[V – W\].
Câu 5. So sánh hai số 11+22+33+…+1\[{0^0}\]01\[{0^0}\]0 và \[{2^{{2^{{2^{{2^2}}}}}}}\]
Hướng dẫn giải
Ta thấy rằng \[{2^{{2^{{2^{{2^2}}}}}}} = {2^{{2^{{2^4}}}}} = {2^{{2^{16}}}}\] mà \[{2^{10}} = 1024 > 1000\] và \[{2^6} = 64\]
Suy ra: \[{2^{16}} = {2^{10}} \cdot {2^6} > 64000\] nên \[{2^{{2^{{2^{{2^2}}}}}}} > {2^{64000}}\]
Mặt khác: \[{1^1} + {2^2} + {3^3} + \ldots + {1000^{1000}}\]\[ < 1000 \cdot {1000^{1000}} = {1000^{1001}}\]\[ < {\left( {{2^{10}}} \right)^{1001}} = {2^{10010}} < {2^{64000}}\]
Từ đó suy ra: \[{1^1} + {2^2} + {3^3} + \ldots + {1000^{1000}} < {2^{{2^{{2^{{2^2}}}}}}}\]
Dạng 3. Rút gọn và biểu diễn các biểu thức chứa luỹ thừa
Câu 1. Rút gọn biểu thức: \[\frac{\begin{gathered}
\hfill \\
\frac{{{a^{1,5}} + {b^{1,5}}}}{{{a^{0,5}} + {b^{0,5}}}} – {a^{0,5}} \cdot {b^{0,5}} \hfill \\
\end{gathered} }{{{a^{0,5}} – {b^{0,5}}}}\]
Hướng dẫn giải
\[\frac{\begin{gathered}
\hfill \\
\frac{{{a^{1,5}} + {b^{1,5}}}}{{{a^{0,5}} + {b^{0,5}}}} – {a^{0,5}} \cdot {b^{0,5}} \hfill \\
\end{gathered} }{{{a^{0,5}} – {b^{0,5}}}}\]\[ = \frac{\begin{gathered}
\hfill \\
\frac{{{{\left( {\sqrt a } \right)}^3} + {{\left( {\sqrt b } \right)}^3}}}{{\sqrt a + \sqrt b }} – \sqrt {ab} \hfill \\
\end{gathered} }{{\sqrt a – \sqrt b }}\]\[ = \frac{{\sqrt a – 2\sqrt {ab} + \sqrt b }}{{\sqrt a – \sqrt b }}\]\[ = \sqrt a – \sqrt b \]
Câu 2. Cho các số thực dương \[a\] và \[b\]. Rút gọn biểu thức: \[P = \frac{{{a^{\frac{1}{3}}}\sqrt b + {b^{\frac{1}{3}}}\sqrt a }}{{\sqrt[6]{a} + \sqrt[6]{b}}} – \sqrt[3]{{ab}}\]
Hướng dẫn giải
\[P = \frac{{{a^{\frac{1}{3}}}\sqrt b + {b^{\frac{1}{3}}}\sqrt a }}{{\sqrt[6]{a} + \sqrt[6]{b}}} – \sqrt[3]{{ab}}\]\[ = \frac{{{a^{\frac{1}{3}}}{b^{\frac{1}{2}}} + {b^{\frac{1}{3}}}{a^{\frac{1}{2}}}}}{{{a^{\frac{1}{6}}} + {b^{\frac{1}{6}}}}} – {\left( {ab} \right)^{\frac{1}{3}}}\]\[ = \frac{{{a^{\frac{1}{3}}}{b^{\frac{1}{3}}}\left( {{b^{\frac{1}{6}}} + {a^{\frac{1}{6}}}} \right)}}{{{a^{\frac{1}{6}}} + {b^{\frac{1}{6}}}}} – {\left( {ab} \right)^{\frac{1}{3}}}\]\[ = {a^{\frac{1}{3}}}{b^{\frac{1}{3}}} – {\left( {ab} \right)^{\frac{1}{3}}}\]\[ = 0\]
Câu 3. Cho \[\alpha \in \left( {0;\frac{\pi }{2}} \right)\]. Rút gọn biểu thức \[{2^{{{\sin }^4}\alpha }} \cdot {2^{{{\cos }^4}\alpha }} \cdot {4^{{{\sin }^2}\alpha \cdot {{\cos }^2}\alpha }}\].
Hướng dẫn giải
\[{2^{{{\sin }^4}\alpha }} \cdot {2^{{{\cos }^4}\alpha }} \cdot {4^{{{\sin }^2}\alpha \cdot {{\cos }^2}\alpha }}\]\[ = {2^{{{\sin }^4}\alpha + {{\cos }^4}\alpha + 2{{\sin }^2}\alpha \cdot {{\cos }^2}\alpha }}\]\[ = {2^{{{\left( {{{\sin }^2}\alpha + {{\cos }^2}\alpha } \right)}^2}}}\]\[ = 2\]
Câu 4. Cho \[b\] là số thực dương. Biểu thức \[\frac{{\sqrt[5]{{{b^2}\sqrt b }}}}{{\sqrt[3]{{b\sqrt b }}}}\] được viết dưới dạng luỹ thừa với số mũ hữu tỉ là bao nhiêu?
Hướng dẫn giải
\[\frac{{\sqrt[5]{{{b^2}\sqrt b }}}}{{\sqrt[3]{{b\sqrt b }}}} = \frac{{\sqrt[5]{{{b^2}{b^{\frac{1}{2}}}}}}}{{\sqrt[3]{{b{b^{\frac{1}{2}}}}}}} = \frac{{\sqrt[5]{{{b^{\frac{5}{2}}}}}}}{{\sqrt[3]{{{b^{\frac{3}{2}}}}}}} = \frac{{{{\left( {{b^{\frac{5}{2}}}} \right)}^{\frac{1}{5}}}}}{{{{\left( {{b^{\frac{3}{2}}}} \right)}^{\frac{1}{3}}}}} = \frac{{{b^{\frac{1}{2}}}}}{{{b^{\frac{1}{2}}}}} = 1\]
Câu 5. Cho hai số thực dương \[a\] và \[b\]. Biểu thức \[\sqrt[5]{{\frac{a}{b}\sqrt[3]{{\frac{b}{a}}}\sqrt {\frac{a}{b}} }}\] được viết dưới dạng luỹ thừa với số mũ hữu tỉ là?
Hướng dẫn giải
\[\sqrt[5]{{\frac{a}{b}\sqrt[3]{{\frac{b}{a}}}\sqrt {\frac{a}{b}} }}\]\[ = \sqrt[5]{{\frac{a}{b}\sqrt[3]{{{{\left( {\frac{a}{b}} \right)}^{ – 1}}{{\frac{a}{b}}^{\frac{1}{2}}}}}}}\]\[ = \sqrt[5]{{\frac{a}{b}\sqrt[3]{{{{\left( {\frac{a}{b}} \right)}^{ – \frac{1}{2}}}}}}}\]\[ = \sqrt[5]{{\frac{a}{b}{{\left( {\frac{a}{b}} \right)}^{ – \frac{1}{6}}}}}\]\[ = \sqrt[5]{{{{\left( {\frac{a}{b}} \right)}^{\frac{5}{6}}}}}\]\[ = {\left( {\frac{a}{b}} \right)^{\frac{1}{6}}}\]
Câu 6. Cho biểu thức \[P = \sqrt {x\sqrt[3]{{{x^2}\sqrt[k]{{{x^3}}}}}} \left( {x > 0} \right)\]. Xác định \[k\] sao cho biểu thức \[P = {x^{\frac{{23}}{{24}}}}\]?
Hướng dẫn giải
Ta có: \[P = \sqrt {x\sqrt[3]{{{x^2}\sqrt[k]{{{x^3}}}}}} = \sqrt {x\sqrt[3]{{{x^{2 + \frac{3}{k}}}}}} = \sqrt {{x^{1 + \frac{{2k + 3}}{{3k}}}}} = {x^{\frac{{5k + 3}}{{6k}}}}\]
Yêu cầu bài toán xảy ra khi: \[\frac{{5k + 3}}{{6k}} = \frac{{23}}{{24}} \Leftrightarrow k = 4\]
Câu 7. Biểu thức thu gọn của \[P = \left( {\frac{{{a^{\frac{1}{2}}} + 2}}{{a + 2{a^{\frac{1}{2}}} + 1}} – \frac{{{a^{\frac{1}{2}}} – 2}}{{a – 1}}} \right) \cdot \frac{{{a^{\frac{1}{2}}} + 1}}{{{a^{\frac{1}{2}}}}}\], \[\left( {a > 0,a \ne \pm 1} \right)\] có dạng \[P = \frac{m}{{a + n}}\]. Tìm biểu thức liên hệ giữa \[m\] và \[n\]?
Hướng dẫn giải
\[P = \left( {\frac{{{a^{\frac{1}{2}}} + 2}}{{a + 2{a^{\frac{1}{2}}} + 1}} – \frac{{{a^{\frac{1}{2}}} – 2}}{{a – 1}}} \right) \cdot \frac{{{a^{\frac{1}{2}}} + 1}}{{{a^{\frac{1}{2}}}}}\]
\[ = \left( {\frac{{\sqrt a + 2}}{{{{\left( {\sqrt a + 1} \right)}^2}}} – \frac{{\sqrt a – 2}}{{\left( {\sqrt a – 1} \right)\left( {\sqrt a + 1} \right)}}} \right) \cdot \frac{{\sqrt a + 1}}{{\sqrt a }}\]
\[ = \left( {\frac{{\sqrt a + 2}}{{\sqrt a + 1}} – \frac{{\sqrt a – 2}}{{\sqrt a – 1}}} \right) \cdot \frac{1}{{\sqrt a }}\]
\[ = \frac{{2\sqrt a }}{{a – 1}} \cdot \frac{1}{{\sqrt a }} = \frac{2}{{a – 1}}\]
Do đó: \[m = 2;n = – 1\]
Vậy \[m = – 2n\]