Lý thuyết
Khái niệm hàm số luỹ thừa
Hàm số \[y = {x^\alpha }\], với \[\alpha \in \mathbb{R}\] được gọi là hàm số luỹ thừa.
Tập xác định của hàm số \[y = {x^\alpha }\] tuỳ thuộc vào giá trị của \[\alpha \]. Cụ thể:
+) \[\alpha \] nguyên dương: \[D = \mathbb{R}\]
+) \[\alpha \] nguyên âm hoặc bằng \[0\]: \[D = \mathbb{R}\backslash \left\{ 0 \right\}\]
+) \[\alpha \] không nguyên: \[D = \left( {0; + \infty } \right)\]
Chú ý:
+) Hàm số luỹ thừa liên tục trên TXĐ của nó
+) Hàm số \[y = {x^{\frac{1}{n}}}\] không đồng nhất với hàm số \[y = \sqrt[n]{x}{\text{ }}\left( {n \in {\mathbb{N}^*}} \right)\]
Ví dụ. Tập xác định của hàm số
\[y = {x^5}\] là \[D = \mathbb{R}\]
\[y = {x^{ – 5}}\] là \[D = \mathbb{R}\backslash \left\{ 0 \right\}\]
\[y = {x^{\frac{2}{7}}},y = {x^\pi }\] là \[D = \left( {0; + \infty } \right)\]
Đạo hàm của hàm số luỹ thừa
+) Hàm số luỹ thừa \[y = {x^\alpha }\] (với \[\alpha \in \mathbb{R}\]) có đạo hàm tại mọi điểm \[x > 0\] và \[({x^\alpha })’ = \alpha \cdot {x^{\alpha – 1}}\]
+) Nếu hàm \[u = u\left( x \right)\] nhận giá trị dương và có đạo hàm trên \[K\] thì hàm số \[y = {u^\alpha }\left( x \right)\] cũng có đạo hàm trên \[K\] và \[{\left[ {{u^\alpha }\left( x \right)} \right]^\prime } = \alpha \cdot {u^{\alpha – 1}}\left( x \right) \cdot u’\left( x \right)\]
Chú ý:
+) Đạo hàm của hàm số căn bậc \[n\]: \[{\left( {\sqrt[n]{x}} \right)^\prime } = \frac{1}{{n\sqrt[n]{{{x^{n – 1}}}}}}\] (\[\forall x > 0\] nếu \[n\] chẵn và \[\forall x \ne 0\] nếu \[n\] lẻ)
+) Nếu hàm số \[u = u\left( x \right)\] có đạo hàm trên \[K\] và thoả mãn điều kiện \[u\left( x \right) > 0,\forall x \in K\] khi \[n\] chẵn và \[u\left( x \right) \ne 0,\forall x \in K\] khi \[n\] lẻ thì
\[{\left( {\sqrt[n]{{u\left( x \right)}}} \right)^\prime } = \frac{{u’\left( x \right)}}{{n\sqrt[n]{{{u^{n – 1}}\left( x \right)}}}}{\text{, }}\left( {\forall x \in K} \right)\]
Khảo sát sự biến thiên và đồ thị của hàm số luỹ thừa
Lưu ý: Khi khảo sát hàm số luỹ thừa với số mũ cụ thể, ta phải xét hàm số đó trên toàn bộ tập xác định của nó. Chẳng hạn: Khảo sát các hàm số \[y = {x^3}\] trên TXĐ của nó là \[\mathbb{R}\], khảo sát hàm số \[y = {x^{ – 2}}\] trên TXĐ \[D = \mathbb{R}\backslash \left\{ 0 \right\}\].

Đồ thị của hàm số
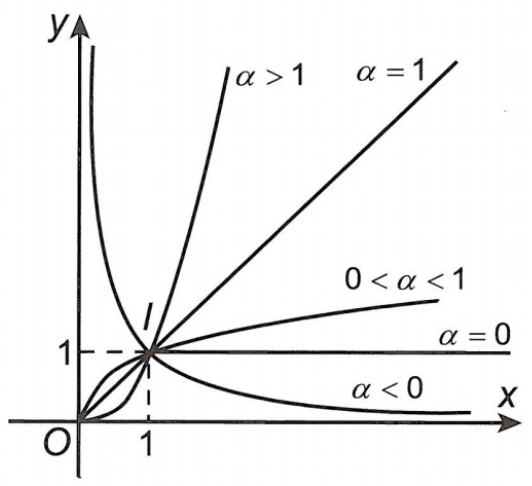
Nhận xét: Đồ thị của hàm số luỹ thừa luôn đi qua điểm \[I\left( {1;1} \right)\].
Sơ đồ hệ thống hoá hàm số luỹ thừa
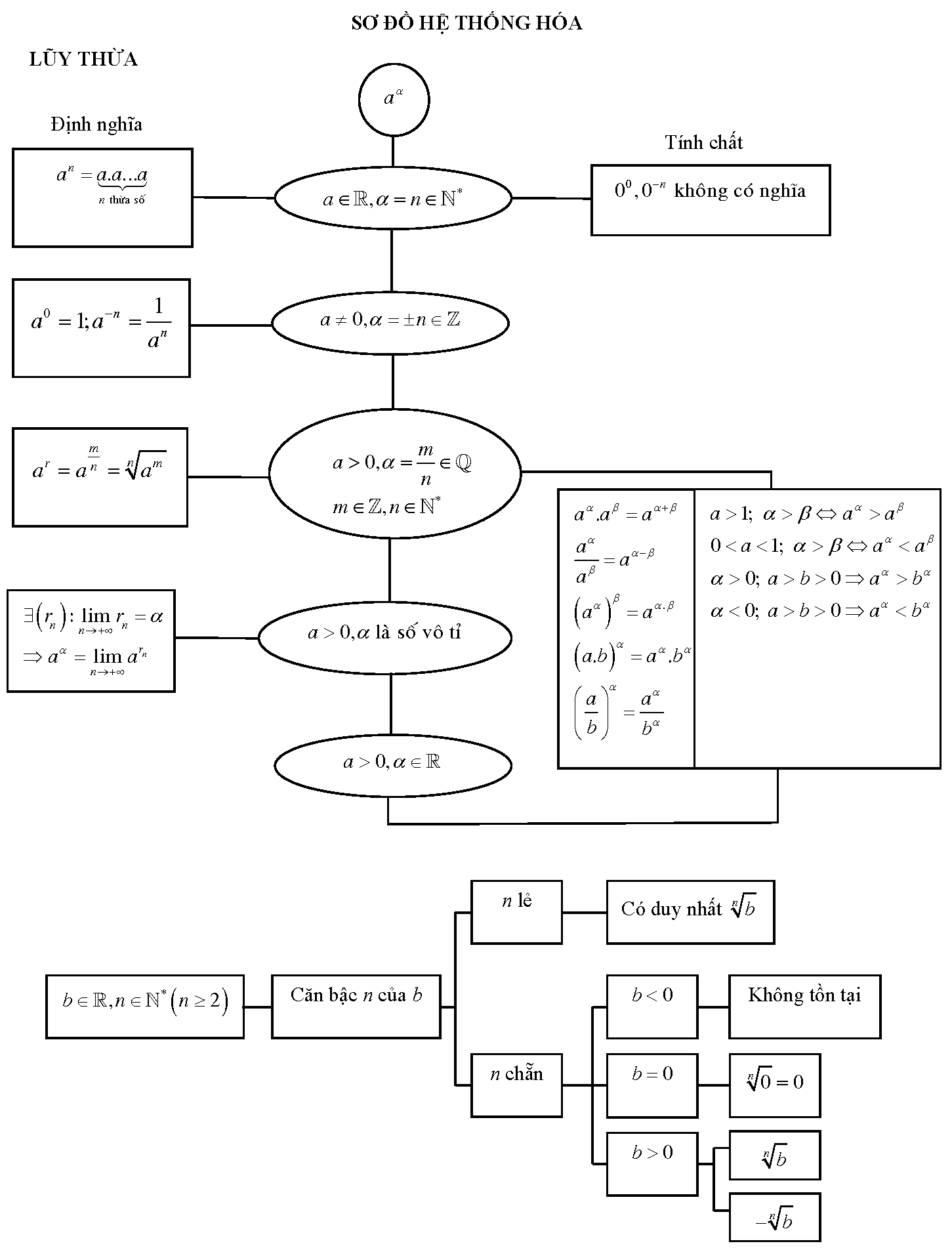
Bài tập tự luận
Dạng 1. Tìm tập xác định của hàm số luỹ thừa
Phương pháp giải
Ta tìm điều kiện xác định của hàm số \[y = {\left[ {f\left( x \right)} \right]^\alpha }\], dựa vào số mũ \[\alpha \] của nó như sau:
+) Nếu \[\alpha \] là số nguyên dương thì không có ĐKXĐ của \[f\left( x \right)\].
+) Nếu \[\alpha \] là số nguyên âm hoặc bằng \[0\] thì ĐKXĐ là \[f\left( x \right) \ne 0\].
+) Nếu \[\alpha \] là số không nguyên thì ĐKXĐ là \[f\left( x \right) > 0\].
Câu 1. Tìm tập xác định của hàm số \[y = {\left( {{x^2} + x – 2} \right)^{ – 3}}\]
Hướng dẫn giải
Vì \[\alpha = – 3 \in {\mathbb{Z}^{^ – }}\] nên hàm số xác định \[ \Leftrightarrow {x^2} + x – 2 \ne 0 \Leftrightarrow \left[ \begin{gathered}
x \ne 1 \hfill \\
x \ne – 2 \hfill \\
\end{gathered} \right.\]
Vậy tập xác định của hàm số là \[D = \mathbb{R}\backslash \left\{ { – 2;1} \right\}\].
Câu 2. Tìm tập xác định của hàm số \[y = {\left( {3{x^2} – 1} \right)^{^{\frac{1}{3}}}}\]
Hướng dẫn giải
Vì \[\alpha = \frac{1}{3} \notin \mathbb{Z}\] nên hàm số xác định \[ \Leftrightarrow 3{x^2} – 1 > 0 \Leftrightarrow \left[ \begin{gathered}
x < – \frac{1}{{\sqrt 3 }}\begin{array}{*{20}{c}}
{} \\
{}
\end{array} \hfill \\
x > \frac{1}{{\sqrt 3 }}\begin{array}{*{20}{c}}
{} \\
{}
\end{array} \hfill \\
\end{gathered} \right.\]
Vậy tập xác định của hàm số là \[D = \left( { – \infty ; – \frac{1}{{\sqrt 3 }}} \right) \cup \left( {\frac{1}{{\sqrt 3 }}; + \infty } \right)\]
Câu 3. Tìm tập xác định của hàm số \[y = {\left( {2 – \sqrt {x – 1} } \right)^{\sqrt 3 }}\]
Hướng dẫn giải
Vì \[\alpha = \sqrt 3 \notin \mathbb{Z}\] nên hàm số xác định \[ \Leftrightarrow 2 – \sqrt {x – 1} > 0\]\[ \Leftrightarrow \sqrt {x – 1} < 2\]\[ \Leftrightarrow \left\{ \begin{gathered}
x – 1 \geqslant 0 \hfill \\
x – 1 < 4 \hfill \\
\end{gathered} \right.\]\[ \Leftrightarrow 1 \leqslant x < 5\]
Vậy tập xác định của hàm số là \[D = \left[ {1;5} \right)\]
Câu 4. Tìm tập xác định của hàm số \[y = {\left( { – {x^2} + 3x + 4} \right)^{\frac{1}{3}}} + \sqrt {2 – x} \]
Hướng dẫn giải
Hàm số xác định khi \[\left\{ \begin{gathered}
– {x^2} + 3x + 4 > 0 \hfill \\
2 – x \geqslant 0 \hfill \\
\end{gathered} \right. \Leftrightarrow \left\{ \begin{gathered}
– 1 < x < 4 \hfill \\
x \leqslant 2 \hfill \\
\end{gathered} \right. \Leftrightarrow – 1 < x \leqslant 2\]
Vậy tập xác định của hàm số là \[D = \left( { – 1;2} \right]\]
Câu 5. Tìm tập hợp các giá trị thực của tham số m để hàm số \[f\left( x \right) = {\left( {2{x^2} + mx + 2} \right)^{\frac{3}{2}}}\] xác định với mọi \[x \in \mathbb{R}\]?
Hướng dẫn giải
Hàm số \[f\left( x \right) = {\left( {2{x^2} + mx + 2} \right)^{\frac{3}{2}}}\] xác định với mọi \[x \in \mathbb{R}\]
\[ \Leftrightarrow 2{x^2} + mx + 2 > 0,{\text{ }}\forall x \in \mathbb{R}\]
\[ \Leftrightarrow \left\{ \begin{gathered}
\Delta < 0 \hfill \\
2 > 0 \hfill \\
\end{gathered} \right. \Leftrightarrow \Delta = {m^2} – 16 < 0\]
\[ \Leftrightarrow – 4 < m < 4 \Leftrightarrow m \in \left( { – 4;4} \right)\]
Dạng 2. Tính đạo hàm của hàm số luỹ thừa
Đạo hàm hàm số luỹ thừa
\[{\left( {{x^\alpha }} \right)^\prime } = \alpha \cdot {x^{\alpha – 1}}{\text{ }}\left( {x > 0,\alpha \in \mathbb{R}} \right)\]
Đạo hàm của hàm hợp
\[{\left( {{u^\alpha }} \right)^\prime } = \alpha \cdot {u^{\alpha – 1}} \cdot u’\] với \[u\] là biểu thức chứa \[x{\text{ }}\left( {u > 0} \right)\]
Câu 1. Tính đạo hàm của hàm số \[y = \sqrt[3]{{{x^2}\sqrt {{x^3}} }}\]
Hướng dẫn giải
Với mọi \[x > 0\], ta có:
\[y = {\left( {\sqrt[3]{{{x^2}\sqrt {{x^3}} }}} \right)^\prime } = {\left( {{x^{\frac{7}{6}}}} \right)^\prime } = \frac{7}{6}{x^{\frac{1}{6}}} = \frac{7}{6}\sqrt[6]{x}\]
Câu 2. Tìm hệ số góc của tiếp tuyến với đồ thị hàm số \[y = {\left( {\sqrt x + 1} \right)^3}\] tại điểm có tung độ bằng \[27\].
Hướng dẫn giải
TXĐ: \[D = \left[ {0; + \infty } \right)\]
\[y = {\left( {\sqrt x + 1} \right)^3} = 27 \Leftrightarrow \sqrt x + 1 = 3 \Leftrightarrow x = 4\]
\[y’ = 3{\left( {\sqrt x + 1} \right)^\prime }{\left( {\sqrt x + 1} \right)^2} = \frac{3}{{2\sqrt x }}{\left( {\sqrt x + 1} \right)^2}\]
\[y’\left( 4 \right) = \frac{3}{{2\sqrt 4 }}{\left( {\sqrt 4 + 1} \right)^2} = \frac{{27}}{4}\]
Vậy hệ số góc của tiếp tuyến tại điểm có tung độ bằng \[27\] là
Câu 3. Cho hàm số \[y = {\left( {x – 1} \right)^{\frac{{3\pi }}{2}}}\] có đồ thị \[\left( C \right)\]. Lấy \[M \in \left( C \right)\] có hoành độ \[{x_0} = 2\]. Tính hệ số góc của tiếp tuyến của \[\left( C \right)\] tại \[M\].
Hướng dẫn giải
TXĐ: \[D = \left( {1; + \infty } \right)\]
Ta có hệ số góc của tiếp tuyến của \[\left( C \right)\] tại \[M\] là \[k = y’\left( 2 \right)\]
\[y’\left( 2 \right) = \frac{{3\pi }}{2} \cdot {1^{\frac{{3\pi }}{2} – 1}} = \frac{{3\pi }}{2}\]
Vậy hệ số góc của tiếp tuyến của \[\left( C \right)\] tại \[M\] là \[k = \frac{{3\pi }}{2}\]
Câu 4. Tính đạo hàm của hàm số \[y = \sqrt {e\sqrt {e\sqrt {e\sqrt {e\sqrt x } } } } ,{\text{ }}x > 0\]
Hướng dẫn giải
Ta có: \[y = {e^{\frac{{15}}{{16}}}} \cdot {x^{\frac{1}{{32}}}}\]
\[y’ = \frac{1}{{32}}{e^{\frac{{15}}{{16}}}} \cdot {x^{\frac{1}{{32}} – 1}} = \frac{1}{{32}}{e^{\frac{{15}}{{16}}}} \cdot {x^{ – \frac{{31}}{{32}}}} = \frac{{{e^{\frac{{15}}{{16}}}}}}{{32\sqrt[{32}]{{{x^{31}}}}}}\]
Câu 5. Cho hàm số \[y = {\left( {x + 2} \right)^{ – 2}}\]. Tìm hệ thức giữa \[y\] và \[{y”}\] không phụ thuộc vào \[x\].
Hướng dẫn giải
TXĐ: \[D = \mathbb{R}\backslash \left\{ { – 2} \right\}\]
\[y’ = – 2 \cdot {\left( {x + 2} \right)^{ – 3}} \cdot {\left( {x + 2} \right)^\prime } = \frac{{ – 2}}{{{{\left( {x + 2} \right)}^3}}}\]
\[y” = 6{\left( {x + 2} \right)^{ – 4}} \cdot {\left( {x + 2} \right)^\prime } = \frac{6}{{{{\left( {x + 2} \right)}^4}}}\]
Vậy hệ thức giữa \[y\] và \[{y”}\] không phụ thuộc vào \[x\] là \[6{y^2} – y” = 0\]
Câu 6. Cho hàm số \[y = \sqrt[3]{{1 + 2\sin 2x}}\]. Tìm đạo hàm của hàm số đã cho tại điểm \[x = 0\].
Hướng dẫn giải
Với \[1 + 2\sin 2x \ne 0\], ta có:
Cách 1: \[y’ = \frac{{4\cos 2x}}{{3\sqrt[3]{{{{\left( {1 + 2\sin 2x} \right)}^2}}}}} \Rightarrow y’\left( 0 \right) = \frac{4}{3}\]
Cách 2: Bấm máy tính 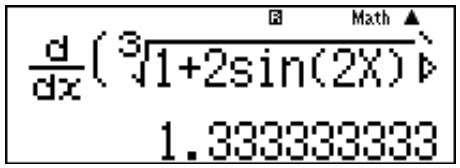
Dạng 3. Khảo sát sự biến thiên và nhận dạng đồ thị của hàm số luỹ thừa
Khảo sát hàm số luỹ thừa với số mũ cụ thể ta phải xét hàm số trên toàn tập xác định.
Tìm tập xác định
TXĐ của hàm luỹ thừa phụ thuộc vào giá trị của \[\alpha \]
Sự biến thiên
+) Tìm đạo hàm \[{y’}\]. Xét dấu \[{y’}\] và kết luận về chiều biến thiên của hàm số.
+) Tìm tiệm cận (nếu có).
+) Lập bảng biến thiên.
Đồ thị
Đồ thị của hàm số luôn đi qua điểm \[\left( {1;1} \right)\]

Câu 1. Khảo sát sự biến thiên và vẽ đồ thị hàm số \[y = {x^2}\].
Hướng dẫn giải
+) TXĐ: \[D = \mathbb{R}\]
+) \[y’ = 2x\]
\[y’ = 0 \Leftrightarrow x = 0\]
+) Giới hạn:
\[\mathop {\lim }\limits_{x \to – \infty } y = + \infty ;\mathop {\lim }\limits_{x \to + \infty } y = + \infty \]
+) Bảng biến thiên:
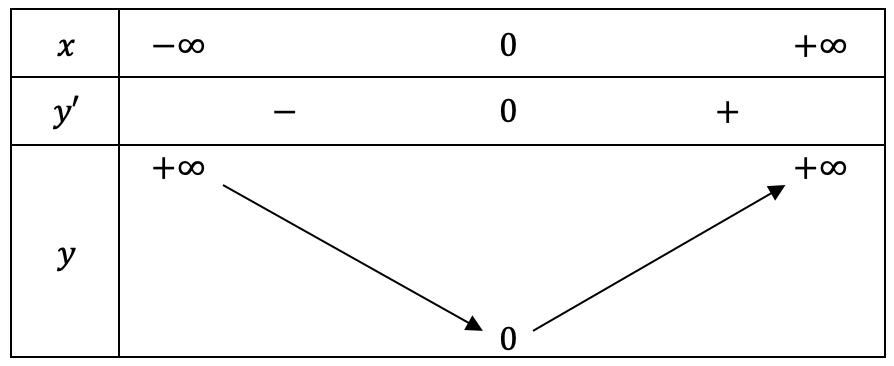
Hàm số đồng biến trên khoảng \[\left( {0; + \infty } \right)\], nghịch biến trên khoảng \[\left( { – \infty ;0} \right)\]
Hàm số đạt cực tiểu tại \[x = 0,{\text{ }}{y_{CT}} = 0\]
Đồ thị hàm số không có tiệm cận.
Đồ thị hàm số đi qua các điểm \[A\left( { – 1;1} \right),B\left( {1;1} \right),C\left( {2;4} \right),D\left( { – 2;4} \right)\]
Hàm số \[y = {x^2}\] là hàm số chẵn nên đồ thị nhận trục tung làm trục đối xứng.
+) Đồ thị:
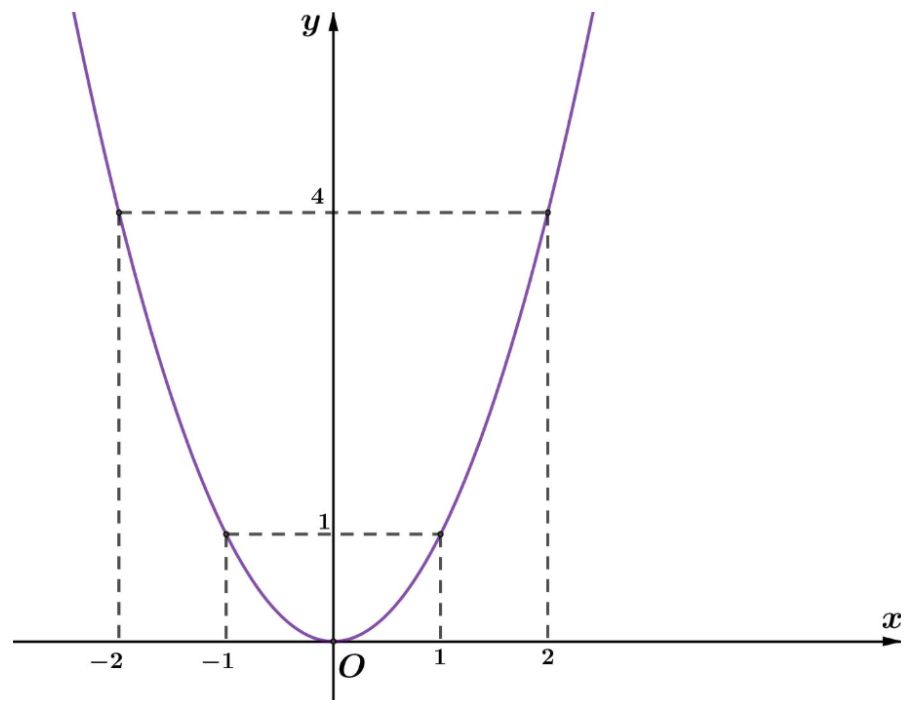
Câu 2. Khảo sát sự biến thiên và vẽ đồ thị hàm số \[y = {x^{ – 1}}\].
Hướng dẫn giải
+) TXĐ: \[D = \mathbb{R}\backslash \left\{ 0 \right\}\]
+) Giới hạn:
\[\mathop {\lim }\limits_{x \to \pm \infty } y = 0;\mathop {\lim }\limits_{x \to {0^ + }} y = + \infty ;\mathop {\lim }\limits_{x \to {0^ – }} y = – \infty \] nên đồ thị hàm số nhận đường thẳng \[y = 0\] làm đường tiệm cận ngang, nhận đường thẳng \[x = 0\] làm đường tiệm cận đứng.
+) Bảng biến thiên:
\[y’ = – {x^{ – 2}} < 0,\forall x \in D\]
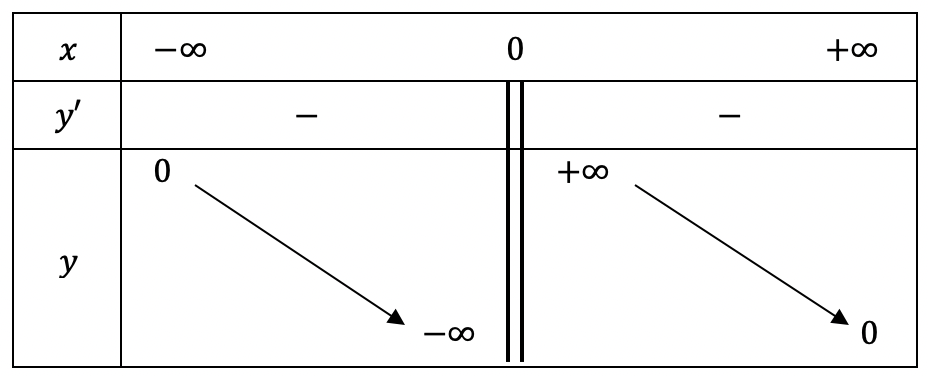
Hàm số nghịch biến trên khoảng \[\left( { – \infty ;0} \right)\] và \[\left( {0; + \infty } \right)\]. Hàm số không có cực trị.
Đồ thị hàm số đi qua các điểm \[A\left( { – 2; – \frac{1}{2}} \right),B\left( { – 1;1} \right),C\left( {1;1} \right),D\left( {2;\frac{1}{2}} \right)\]
Hàm số \[y = {x^{ – 1}}\] là hàm số lẻ nên đồ thị nhận gốc toạ độ làm tâm đối xứng.
+) Đồ thị:
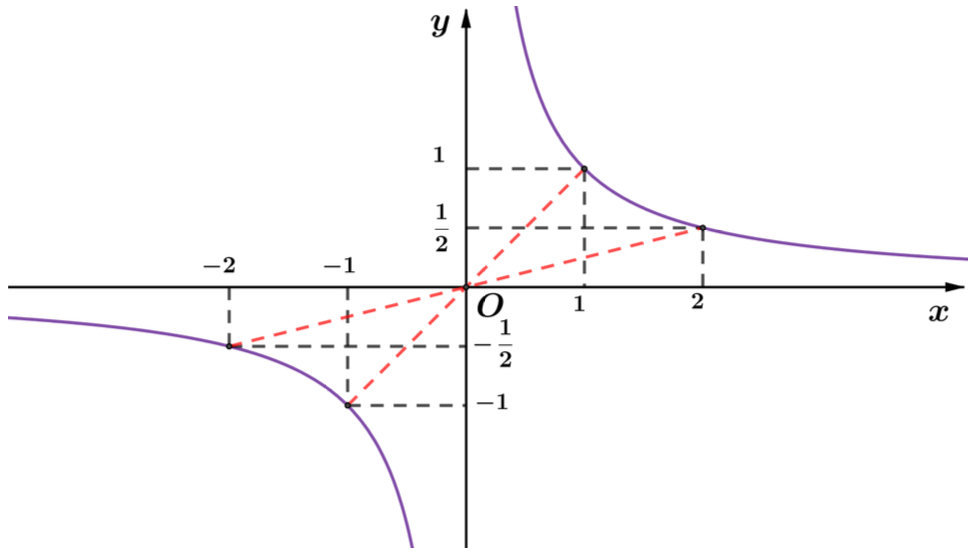
Câu 3. Khảo sát sự biến thiên và vẽ đồ thị hàm số \[y = {\left( {x – 2} \right)^{ – 4}}\].
Hướng dẫn giải
+) TXĐ: \[D = \mathbb{R}\backslash \left\{ 2 \right\}\]
+) Giới hạn:
\[\mathop {\lim }\limits_{x \to \pm \infty } y = 0\]. Đồ thị hàm số nhận đường thẳng \[y = 0\] làm đường tiệm cận ngang
\[\mathop {\lim }\limits_{x \to {2^ \pm }} y = + \infty \]. Đồ thị hàm số nhận đường thẳng \[x = 2\] làm đường tiệm cận đứng.
+) Bảng biến thiên:
\[y’ = – 4 \cdot {\left( {x – 2} \right)^{ – 5}}\]
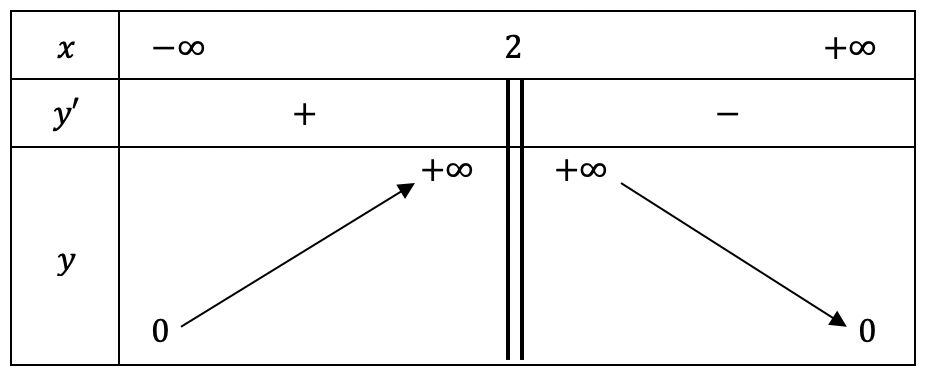
Hàm số đồng biến trên khoảng \[\left( { – \infty ;2} \right)\] và nghịch biến trên khoảng \[\left( {2; + \infty } \right)\].
Hàm số không có cực trị.
Đồ thị hàm số đi qua các điểm \[A\left( {0;\frac{1}{{16}}} \right),B\left( {1;1} \right),C\left( {3;1} \right)\] và nhận đường thẳng \[x = 2\] làm trục đối xứng.
+) Đồ thị:
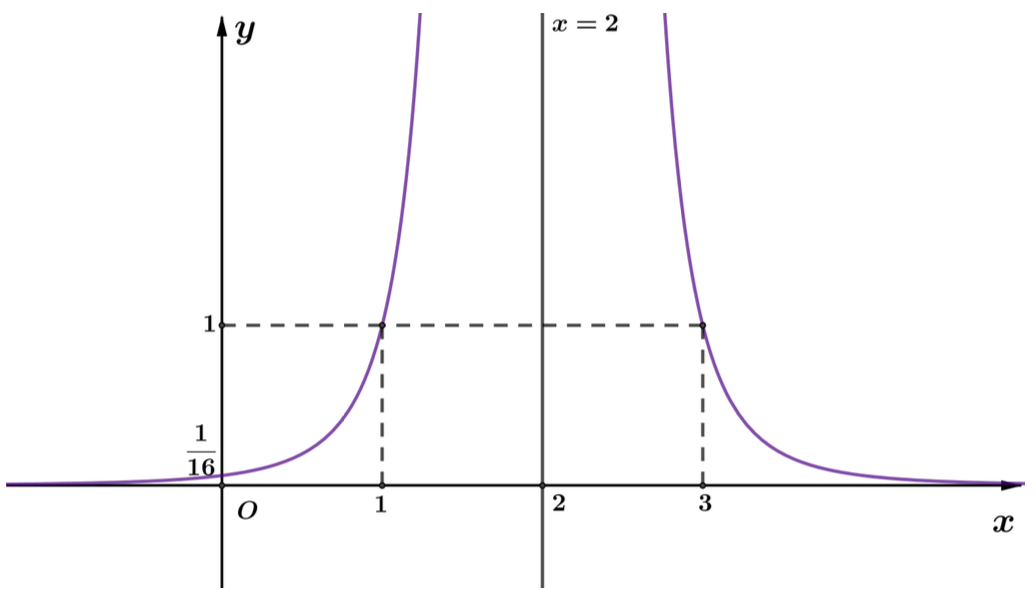
Câu 4. Khảo sát sự biến thiên và vẽ đồ thị hàm số \[y = {x^{\frac{1}{2}}}\].
Hướng dẫn giải
+) TXĐ: \[D = \left( {0; + \infty } \right)\]
+) Giới hạn:
\[\mathop {\lim }\limits_{x \to + \infty } y = + \infty ,\mathop {\lim }\limits_{x \to {0^ + }} y = 0\] nên đồ thị hàm số không có đường tiệm cận.
+) Bảng biến thiên:
\[y’ = \frac{1}{2}{x^{ – \frac{1}{2}}} > 0,\forall x \in D\]
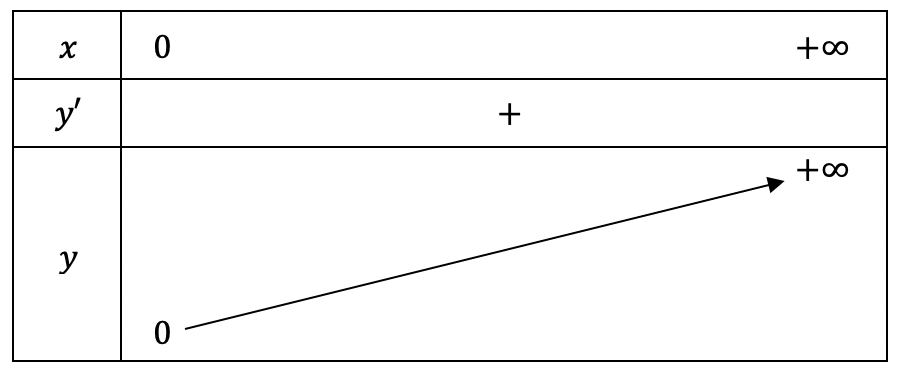
Hàm số đồng biến trên khoảng \[\left( {0; + \infty } \right)\].
Hàm số không có cực trị.
Đồ thị hàm số đi qua các điểm \[A\left( {1;1} \right),B\left( {2;\sqrt 2 } \right),C\left( {4;2} \right)\]
+) Đồ thị:
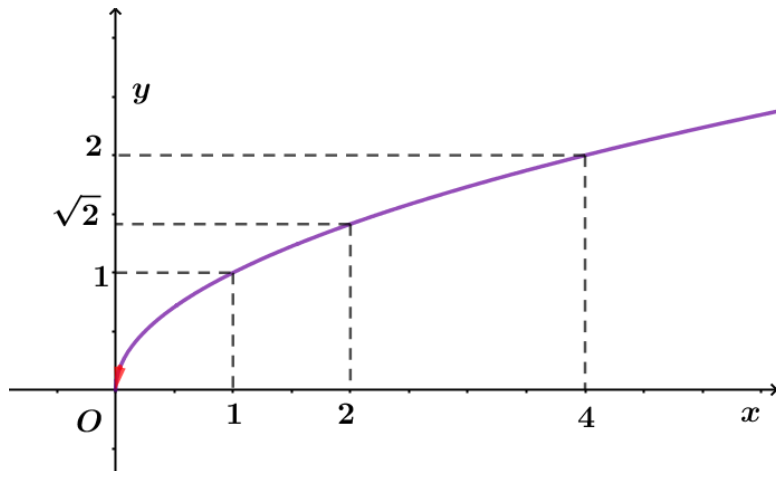
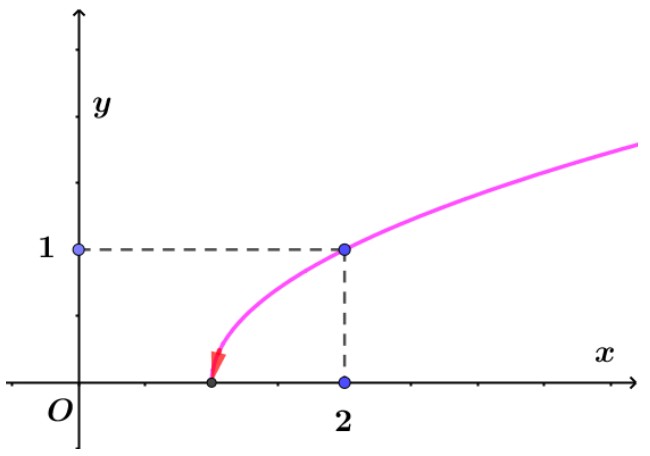
Câu 5. Khảo sát sự biến thiên và vẽ đồ thị hàm số \[y = {\left( {x – 1} \right)^{\frac{1}{2}}}\].
Hướng dẫn giải
+) TXĐ: \[D = \left( {1; + \infty } \right)\]
+) Giới hạn:
\[\mathop {\lim }\limits_{x \to + \infty } y = + \infty ,\mathop {\lim }\limits_{x \to {1^ + }} y = 0\] nên đồ thị hàm số không có đường tiệm cận.
+) Bảng biến thiên:
\[y’ = \frac{1}{4}{\left( {x – 1} \right)^{ – \frac{3}{4}}} > 0,\forall x \in D\]
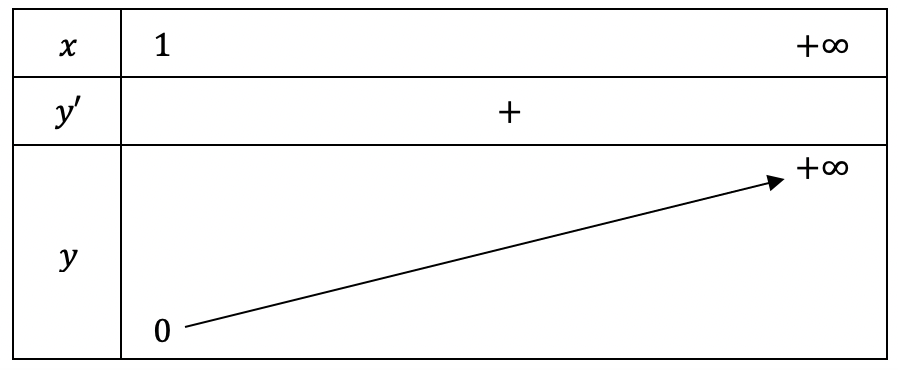
Hàm số đồng biến trên khoảng \[\left( {1; + \infty } \right)\].
Hàm số không có cực trị.
Đồ thị hàm số đi qua các điểm \[A\left( {2;1} \right)\]
+) Đồ thị:
Câu 6. Khảo sát sự biến thiên và vẽ đồ thị hàm số \[y = {x^{ – \sqrt 2 }}\].
Hướng dẫn giải
+) TXĐ: \[D = \left( {0; + \infty } \right)\]
+) Giới hạn:
\[\mathop {\lim }\limits_{x \to {0^ + }} \frac{1}{{{x^{\sqrt 2 }}}} = + \infty \]. Đồ thị hàm số nhận trục \[Oy\] \[\left( {x = 0} \right)\] là đường tiệm cận đứng.
\[\mathop {\lim }\limits_{x \to + \infty } \frac{1}{{{x^{\sqrt 2 }}}} = 0\]. Đồ thị hàm số nhận trục \[Ox\] \[\left( {y = 0} \right)\] là đường tiệm cận ngang.
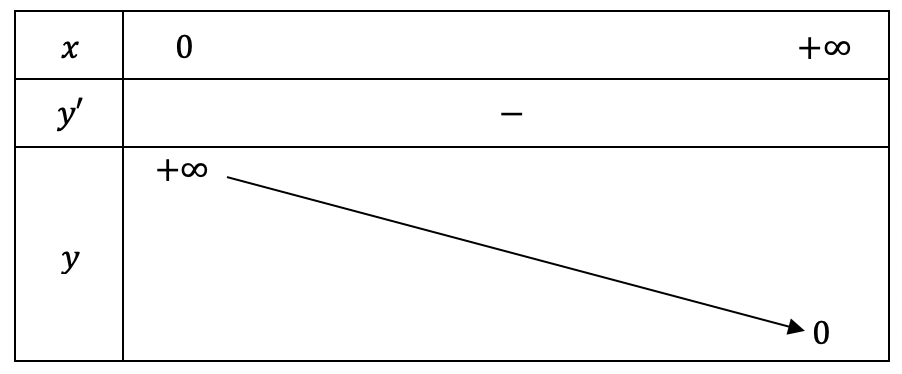
+) \[y’ = – \sqrt 2 {x^{ – \sqrt 2 – 1}} < 0,\forall x \in D\]
Hàm số đã cho nghịch biến trên khoảng \[\left( {0; + \infty } \right)\]
+) Bảng biến thiên:
+) Đồ thị:
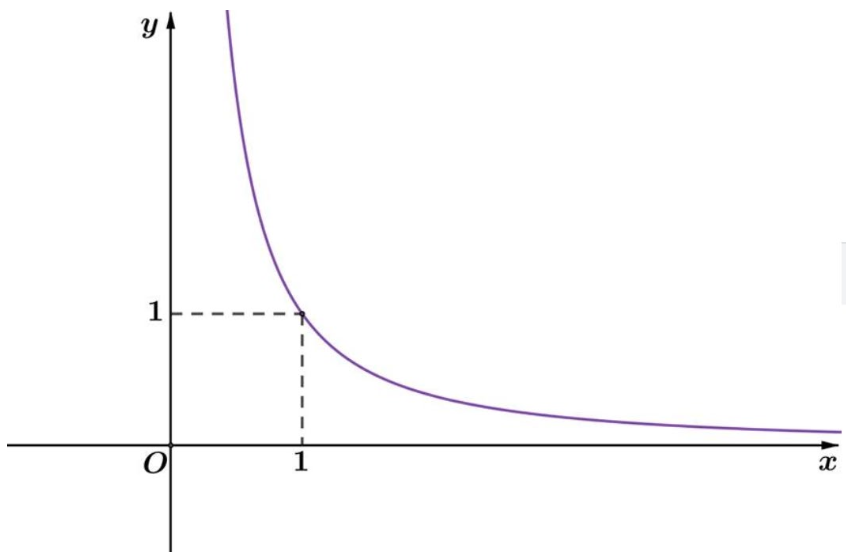
Đồ thị hàm số đi qua điểm \[\left( {1;1} \right)\].