Lý thuyết
Nhánh vô cực của đường cong \[\left( C \right):y = f\left( x \right)\]
Gọi \[M\left( {x;y} \right) \in \left( C \right)\]
Ta nói: \[\left( C \right)\] có nhánh vô cực \[ \Leftrightarrow \left[ \begin{gathered}
x \to + \infty {\text{ }}hay{\text{ }}x \to – \infty \hfill \\
y \to + \infty {\text{ }}hay{\text{ }}y \to – \infty \hfill \\
\end{gathered} \right.\]
Ví dụ 1. Đồ thị \[\left( C \right)\] của hàm số \[y = {x^2}\] có nhánh vô cực
Ví dụ 2. Đồ thị \[\left( C \right)\] của hàm số \[y = \sqrt {4 – {x^2}} \] không có nhánh vô cực
vì \[M\left( {x;y} \right) \in \left( C \right) \Rightarrow \left\{ \begin{gathered}
– 2 \leqslant x \leqslant 2 \hfill \\
0 \leqslant y \leqslant 2 \hfill \\
\end{gathered} \right.\]
Tiệm cận của đường cong
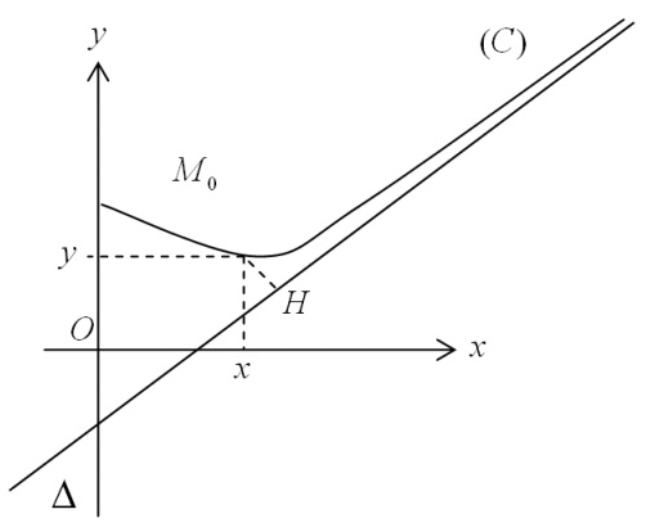
Cho đường cong \[\left( C \right):y = f\left( x \right)\] và \[M\left( {x;y} \right) \in \left( C \right)\], \[H\] là hình chiếu vuông góc của \[M\] lên \[\left( \Delta \right)\]. Đường thẳng \[\left( \Delta \right)\] được gọi là tiệm cận của \[\left( C \right)\] khi và chỉ khi khoảng cách \[MH\] từ \[M\] đến \[\left( \Delta \right)\] tiến về 0 khi \[M\] vẽ nên nhánh vô cực của \[\left( C \right)\].
Như vậy: \[\left( \Delta \right)\] tiệm cận của \[\left( C \right) \Leftrightarrow \mathop {\lim }\limits_{M \to \infty } MH = 0\]
Định nghĩa đường tiệm cận đứng và tiệm cận ngang của đồ thị hàm số
Tiệm cận đứng của đồ thị hàm số
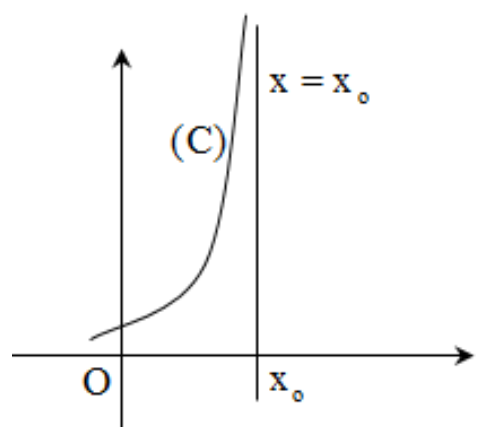
Đường thẳng \[x = {x_0}\] được gọi là đường tiệm cận đứng (TCĐ) của đồ thị hàm số \[y = f\left( x \right)\] nếu thoả mãn ít nhất một trong các điều kiện sau:
\[\mathop {\lim }\limits_{x \to x_0^ + } f\left( x \right) = + \infty ;{\text{ }}\mathop {\lim }\limits_{x \to x_0^ + } f\left( x \right) = – \infty \]
\[\mathop {\lim }\limits_{x \to x_0^ – } f\left( x \right) = + \infty ;{\text{ }}\mathop {\lim }\limits_{x \to x_0^ – } f\left( x \right) = – \infty \]
Tiệm cận ngang của đồ thị hàm số
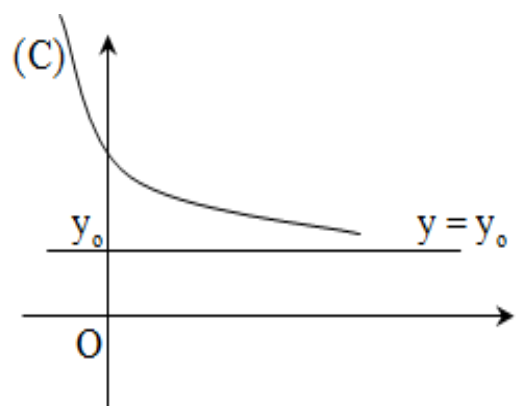
Cho hàm số \[y = f\left( x \right)\] có xác định trên một khoảng vô hạn là khoảng có một trong các dạng \[\left( {a; + \infty } \right);\left( { – \infty ;a} \right);\left( { – \infty ; + \infty } \right)\]. Đường thẳng \[y = {y_0}\] được gọi là đường tiệm cận ngang (TCN) của đồ thị nếu thoả mãn ít nhất một trong các điều kiện sau:
\[\mathop {\lim }\limits_{x \to – \infty } f\left( x \right) = {y_0};{\text{ }}\mathop {\lim }\limits_{x \to + \infty } f\left( x \right) = {y_0}\]
Lưu ý:
☞ Hàm \[y = \frac{{ax + b}}{{cx + d}}\] với \[ac \ne 0\] có tiệm cận đứng \[x = – \frac{d}{c}\]; tiệm cận ngang \[y = \frac{a}{c}\]
☞ Hàm \[y = \frac{{f\left( x \right)}}{{g\left( x \right)}}\] với \[{f\left( x \right)}\], \[{g\left( x \right)}\] là những hàm đa thức
+) Nếu bậc tử nhỏ hơn bậc mẫu thì có tiệm cận ngang \[y = 0\].
+) Nếu bậc tử bằng bậc mẫu thì có tiệm cận ngang \[y = \frac{{{a_n}}}{{{b_n}}}\] với \[{a_n},{b_n}\] là hệ số của luỹ thừa cao nhất trên tử và dưới mẫu.
+) Nếu bậc tử lớn hơn bậc mẫu thì không có tiệm cận ngang.
+) \[x = {x_0}\] là tiệm cận đứng \[ \Leftrightarrow \left[ \begin{gathered}
g\left( {{x_0}} \right) = 0;f\left( {{x_0}} \right) \ne 0 \hfill \\
\left\{ \begin{gathered}
g\left( {{x_0}} \right) = f\left( {{x_0}} \right) = 0\begin{array}{*{20}{c}}
{} \\
{}
\end{array} \hfill \\
\mathop {\lim }\limits_{x \to {x_0}} \frac{{f\left( x \right)}}{{g\left( x \right)}} = \pm \infty \hfill \\
\end{gathered} \right. \hfill \\
\end{gathered} \right.\]
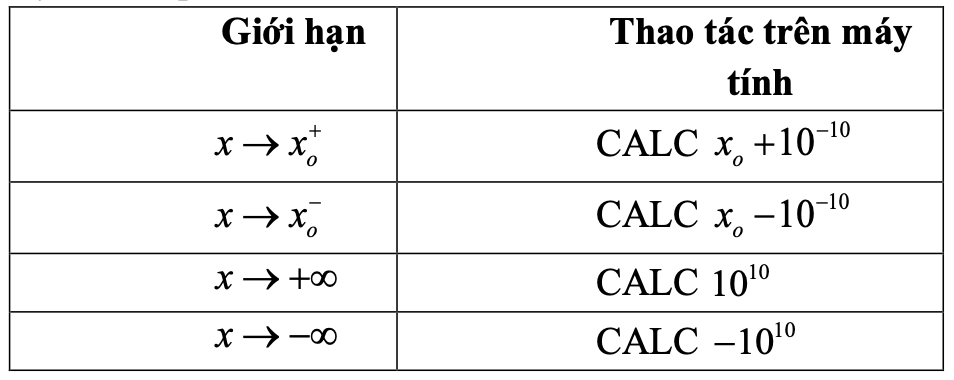
☞ Ứng dụng máy tính CASIO để tìm tiệm cận đứng hoặc tiệm cận ngang.
Để tìm tiệm cận đứng hoặc tiệm cận ngang của một hàm số thông qua máy tính CASIO, ta sử dụng phím CALC trên máy.
Một số lưu ý về kết quả và cách bấm:
Bài tập tự luận
Dạng 1. Tìm tiệm cận của đồ thị hàm số cho bởi công thức
Câu 1. Cho hàm số \[y = f\left( x \right) = \frac{{2x – 3}}{{x + 2}}\]. Tìm tổng số đường tiệm cận ngang và tiệm cận đứng của đồ thị hàm số \[y = f\left( x \right)\].
Hướng dẫn giải
Vì \[\mathop {\lim }\limits_{x \to – \infty } y = 2;\mathop {\lim }\limits_{x \to + \infty } y = 2\] nên đồ thị hàm số có 1 TCN là \[y = 2\].
Vì \[\mathop {\lim }\limits_{x \to – {2^ + }} y = – \infty ;\mathop {\lim }\limits_{x \to – {2^ – }} y = + \infty \] nên đồ thị hàm số có 1 TCĐ là \[x = – 2\]
Do đó đồ thị hàm số có tổng số 2 tiệm cận kể cả đứng và ngang.
Câu 2. Cho hàm số \[y = \frac{{5x + 1 – \sqrt {x + 1} }}{{{x^2} + 2x}}\]. Tìm tổng số đường tiệm cận ngang và tiệm cận đứng của đồ thị hàm số.
Hướng dẫn giải
TXĐ: \[D = \left[ { – 1; + \infty } \right)\backslash \left\{ 0 \right\}\]
Vì \[\mathop {\lim }\limits_{x \to + \infty } y = \mathop {\lim }\limits_{x \to + \infty } \frac{{5x + 1 – \sqrt {x + 1} }}{{{x^2} + 2x}} = \mathop {\lim }\limits_{x \to + \infty } \frac{\begin{gathered}
\hfill \\
\frac{5}{x} + \frac{1}{{{x^2}}} – \sqrt {\frac{1}{{{x^3}}} + \frac{1}{{{x^4}}}} \hfill \\
\end{gathered} }{\begin{gathered}
1 + \frac{2}{x} \hfill \\
\hfill \\
\end{gathered} }\]
\[ \Rightarrow y = 0\] là đường tiệm cận ngang của đồ thị hàm số.
Vì \[\mathop {\lim }\limits_{x \to 0} y = \mathop {\lim }\limits_{x \to 0} \frac{{5x + 1 – \sqrt {x + 1} }}{{{x^2} + 2x}}\]
\[ = \mathop {\lim }\limits_{x \to 0} \frac{{{{\left( {5x + 1} \right)}^2} – x – 1}}{{\left( {{x^2} + 2x} \right)\left( {5x + 1 + \sqrt {x + 1} } \right)}}\]
\[ = \mathop {\lim }\limits_{x \to 0} \frac{{25{x^2} + 9x}}{{\left( {{x^2} + 2x} \right)\left( {5x + 1 + \sqrt {x + 1} } \right)}}\]
\[ = \mathop {\lim }\limits_{x \to 0} \frac{{25x + 9}}{{\left( {x + 2} \right)\left( {5x + 1 + \sqrt {x + 1} } \right)}}\]\[ = \frac{{ – 9}}{4}\]
\[ \Rightarrow x = 0\] không là đường tiệm cận đứng của đồ thị hàm số.
Do đó đồ thị hàm số có tổng số 1 đường tiệm cận.
Câu 3. Cho hàm số \[f\left( x \right) = \frac{{x + 1}}{{\sqrt {{x^2} – 1} }}\]. Tìm tổng số đường tiệm cận ngang và tiệm cận đứng của đồ thị hàm số.
Hướng dẫn giải
TXĐ: \[D = \left( { – \infty ; – 1} \right) \cup \left( {1; + \infty } \right)\]
TH1: \[x < – 1 \Rightarrow x + 1 < 0\]. Khi đó:
\[f\left( x \right) = \frac{{x + 1}}{{\sqrt {{x^2} – 1} }} = \frac{{ – \sqrt {{{\left( {x + 1} \right)}^2}} }}{{\sqrt {\left( {x – 1} \right)\left( {x + 1} \right)} }} = – \sqrt {\frac{{x + 1}}{{x – 1}}} \]
Suy ra hàm số có TCN là \[y = – 1\], không có TCĐ.
TH2: \[x > 1 \Rightarrow x + 1 > 0\]. Khi đó:
\[f\left( x \right) = \frac{{x + 1}}{{\sqrt {{x^2} – 1} }} = \frac{{\sqrt {{{\left( {x + 1} \right)}^2}} }}{{\sqrt {\left( {x – 1} \right)\left( {x + 1} \right)} }} = \sqrt {\frac{{x + 1}}{{x – 1}}} \]
Suy ra hàm số có TCN là \[y = 1\], TCĐ là \[x = 1\]
Vậy hàm số có 2 TCN và 1 TCĐ
Câu 4. Cho hàm số \[y = \frac{{{x^2} + 2x + 3}}{{\sqrt {{x^4} – 3{x^2} + 2} }}\]. Tìm tổng số đường tiệm cận ngang và tiệm cận đứng của đồ thị hàm số.
Hướng dẫn giải
Điều kiện: \[x \in \left( { – \infty ; – \sqrt 2 } \right) \cup \left( { – 1;1} \right) \cup \left( {\sqrt 2 ; + \infty } \right)\]
Do \[\mathop {\lim }\limits_{x \to + \infty } y = \mathop {\lim }\limits_{x \to – \infty } y = \mathop {\lim }\limits_{x \to \pm \infty } \frac{{{x^2} + 2x + 3}}{{\sqrt {{x^4} – 3{x^2} + 2} }}\]\[ = \mathop {\lim }\limits_{x \to \pm \infty } \frac{\begin{gathered}
\hfill \\
1 + \frac{2}{x} + \frac{3}{{{x^2}}} \hfill \\
\end{gathered} }{\begin{gathered}
\sqrt {1 – \frac{3}{{{x^2}}} + \frac{2}{{{x^4}}}} \hfill \\
\hfill \\
\end{gathered} } = 1\]
\[ \Rightarrow y = 1\] là đường tiệm cận ngang của đồ thị hàm số.
Có \[\mathop {\lim }\limits_{x \to {1^ – }} y = + \infty \]
\[ \Rightarrow x = 1\] là đường tiệm cận đứng của đồ thị hàm số.
Có \[\mathop {\lim }\limits_{x \to {{\left( { – 1} \right)}^ + }} y\]\[ = \mathop {\lim }\limits_{x \to {{\left( { – 1} \right)}^ + }} \frac{{\left( {x + 1} \right)\left( {x + 2} \right)}}{{\sqrt {\left( {x + 1} \right)\left( {x + \sqrt 2 } \right)\left( {x – 1} \right)\left( {x – \sqrt 2 } \right)} }}\]
\[ = \mathop {\lim }\limits_{x \to {{\left( { – 1} \right)}^ + }} \frac{{\sqrt {\left( {x + 1} \right)} \left( {x + 2} \right)}}{{\sqrt {\left( {x + \sqrt 2 } \right)\left( {x – 1} \right)\left( {x – \sqrt 2 } \right)} }}\]\[ = 0\]
\[ \Rightarrow x = – 1\] không là đường tiệm cận đứng của đồ thị hàm số.
Có \[\mathop {\lim }\limits_{x \to {{\left( {\sqrt 2 } \right)}^ + }} y = + \infty \]
\[ \Rightarrow x = \sqrt 2 \] là đường tiệm cận đứng của đồ thị hàm số.
Có \[\mathop {\lim }\limits_{x \to {{\left( { – \sqrt 2 } \right)}^ – }} y = + \infty \]
\[ \Rightarrow x = – \sqrt 2 \] là đường tiệm cận đứng của đồ thị hàm số.
Vậy đồ thị hàm số có 4 đường tiệm cận (1 TCN và 3 TCĐ).
Dạng 2. Tìm tiệm cận của đồ thị hàm số biết BBT của hàm số, đồ thị của hàm số đó hoặc hàm số liên quan
Câu 1. Cho hàm số \[y = f\left( x \right)\] có bảng biến thiên

Tìm tổng số đường TCN và TCĐ của đồ thị hàm số \[y = f\left( x \right)\].
Hướng dẫn giải
Vì \[\mathop {\lim }\limits_{x \to – \infty } y = – \infty ;\mathop {\lim }\limits_{x \to + \infty } y = 3\] nên đồ thị hàm số có 1 TCN là \[y = 3\].
Vì \[\mathop {\lim }\limits_{x \to x_4^ + } y = + \infty \] nên đồ thị hàm số có 1 TCĐ \[x = {x_4}\].
Do đó đồ thị hàm số có tổng số 2 tiệm cận.
Câu 2. Cho hàm số \[y = f\left( x \right)\] xác định trên \[\mathbb{R}\backslash \left\{ 0 \right\}\], liên tục trên mỗi khoảng xác định và có bảng biến thiên như sau:
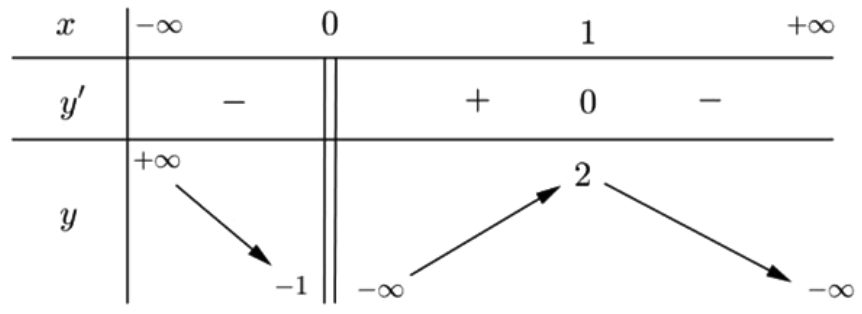
Hỏi đồ thị hàm số trên có bao nhiêu đường TCĐ và TCN?
Hướng dẫn giải
TXĐ: \[D = \mathbb{R}\backslash \left\{ 0 \right\}\]
Ta có:
\[\mathop {\lim }\limits_{x \to – \infty } f\left( x \right) = + \infty ;\mathop {\lim }\limits_{x \to + \infty } f\left( x \right) = – \infty \] do đó đồ thị hàm số không có tiệm cận ngang.
\[\mathop {\lim }\limits_{x \to {0^ + }} f\left( x \right) = – \infty \Rightarrow x = 0\] là đường tiệm cận đứng duy nhất của đồ thị hàm số.
Câu 3. Cho hàm số \[y = f\left( x \right)\] xác định trên \[\mathbb{R}\backslash \left\{ 1 \right\}\], liên tục trên mỗi khoảng xác định và có bảng biến thiên như sau:
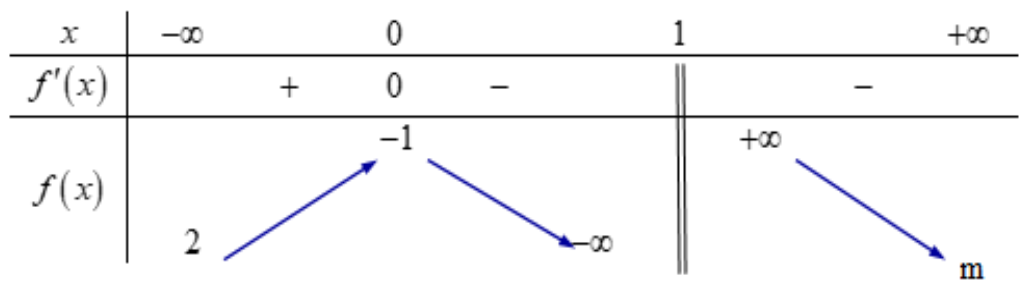
Tìm các giá trị nguyên của \[m \in \left[ {0;5} \right)\] để đồ thị hàm số \[y = f\left( x \right)\] có 3 đường TCĐ và TCN?
Hướng dẫn giải
TXĐ: \[D = \mathbb{R}\backslash \left\{ 1 \right\}\]
Ta có:
\[\mathop {\lim }\limits_{x \to – \infty } f\left( x \right) = 2 \Rightarrow y = 2\] là đường tiệm cận ngang.
\[\mathop {\lim }\limits_{x \to {1^ – }} f\left( x \right) = – \infty \Rightarrow x = 1\] là tiệm cận đứng.
\[\mathop {\lim }\limits_{x \to + \infty } f\left( x \right) = m \Rightarrow y = m\] là đường tiệm cận ngang.
Do đó: Để đồ thị hàm số có 3 đường TCN thì \[m \ne 2\], mà \[m \in \left[ {0;5} \right)\] nên \[m \in \left\{ {0;1;3;4} \right\}\].
Câu 4. Cho hàm số \[{f\left( x \right)}\] có đồ thị như hình vẽ bên.
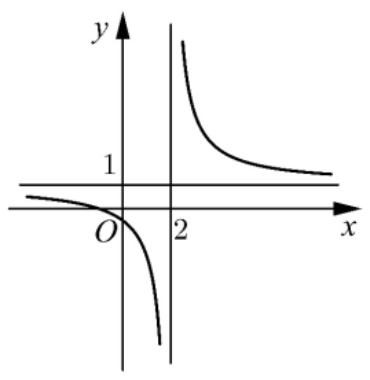
Tìm phương trình các đường TCĐ và TCN của đồ thị hàm số trên.
Hướng dẫn giải
Nhìn vào đồ thị, ta có: \[\mathop {\lim }\limits_{x \to {2^ – }} f\left( x \right) = – \infty \] và \[\mathop {\lim }\limits_{x \to {2^ + }} f\left( x \right) = + \infty \]. Do đó, đồ thị có một TCĐ là đường thẳng \[x = 2\].
Theo đồ thị, ta cũng có: \[\mathop {\lim }\limits_{x \to – \infty } f\left( x \right) = 1\] và \[\mathop {\lim }\limits_{x \to + \infty } f\left( x \right) = 1\]. Do đó, đồ thị có một TCN là đường thẳng \[y = 1\].
Vậy đồ thị có TCĐ \[x = 2\] và TCN \[y = 1\].
Câu 5. Cho đồ thị hàm số \[y = f\left( x \right)\] như hình bên. Đồ thị có bao nhiêu đường TCĐ và TCN?
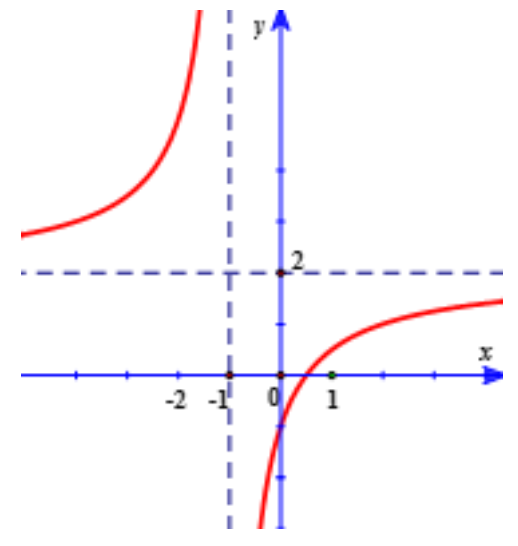
Hướng dẫn giải
Nhìn vào đồ thị, ta có: \[\mathop {\lim }\limits_{x \to – {1^ – }} f\left( x \right) = + \infty \] và \[\mathop {\lim }\limits_{x \to – {1^ + }} f\left( x \right) = – \infty \]. Do đó, đồ thị có một TCĐ là đường thẳng \[x = – 1\].
Theo đồ thị, ta cũng có: \[\mathop {\lim }\limits_{x \to – \infty } f\left( x \right) = 2\] và \[\mathop {\lim }\limits_{x \to + \infty } f\left( x \right) = 2\]. Do đó, đồ thị có một TCN là đường thẳng \[y = 2\].
Vậy đồ thị có TCĐ \[x = – 1\] và TCN \[y = 2\].
Dạng 3. Tiệm cận của đồ thị hàm số hàm hợp
Các dạng trong chủ đề: Cho hàm số \[y = f\left( x \right)\] biết bảng biến thiên hoặc đồ thị. Tìm các đường TCĐ và TCN của đồ thị \[y = g\left( x \right)\] thuộc một trong các dạng sau:
+) \[{y = f\left( {u\left( x \right)} \right)}\]
+) \[y = g\left( {f\left( x \right)} \right)\]
+) \[y = g\left( {f\left( {u\left( x \right)} \right)} \right)\]
+) \[y = g\left( {x,f\left( x \right)} \right)\]
+) \[y = g\left( {x,f\left( {u\left( x \right)} \right)} \right)\]
Phương pháp giải
Gọi \[\left( G \right)\] là đồ thị hàm số \[y = g\left( x \right)\].
* Tìm tiệm cận ngang
Xét hàm số dạng \[g\left( x \right) = \frac{{u\left( x \right)}}{{v\left( x \right)}}\]. Một dấu hiệu thường dùng để nhận biết \[\left( G \right)\] có tiệm cận ngang:
+) Hàm số \[y = g\left( x \right)\] xác định trên \[\left( {a; + \infty } \right)\] hoặc trên \[\left( { – \infty ;a} \right)\]
+) Bậc của \[u\left( x \right)\] \[ \leqslant \] Bậc của \[{v\left( x \right)}\]
+) \[\mathop {\lim }\limits_{x \to + \infty } g\left( x \right) = {y_0}\] hoặc \[\mathop {\lim }\limits_{x \to – \infty } g\left( x \right) = {y_0}\] \[ \Rightarrow \] Đường thẳng \[y = {y_0}\] là tiệm cận ngang của \[\left( G \right)\].
* Tìm tiệm cận đứng
Xét hàm số dạng \[g\left( x \right) = \frac{{u\left( x \right)}}{{v\left( x \right)}}\]. Một dấu hiệu thường dùng để nhận biết \[x = {x_0}\] là tiệm cận đứng của \[\left( G \right)\]:
+) \[v\left( {{x_0}} \right) = 0\] và \[u\left( {{x_0}} \right) \ne 0\], \[{g\left( x \right)}\] xác định trên \[\left( {a;{x_0}} \right)\] hoặc \[\left( {{x_0};b} \right)\].
+) Ít nhất một trong hai giới hạn \[\mathop {\lim }\limits_{x \to x_0^ + } g\left( x \right),\mathop {\lim }\limits_{x \to x_0^ – } g\left( x \right)\] là giới hạn vô cực.
\[ \Rightarrow \] Đường thẳng \[x = {x_0}\] là tiệm cận đứng của \[\left( G \right)\].
Trong chủ đề này, các dấu hiệu nhận biết ở trên dựa vào bảng biến thiên hoặc đồ thị của hàm số \[y = f\left( x \right)\].
Câu 1. Cho hàm đồ \[y = f\left( x \right)\] liên tục trên \[\mathbb{R}\backslash \left\{ 1 \right\}\] và có bảng biến thiên như sau:
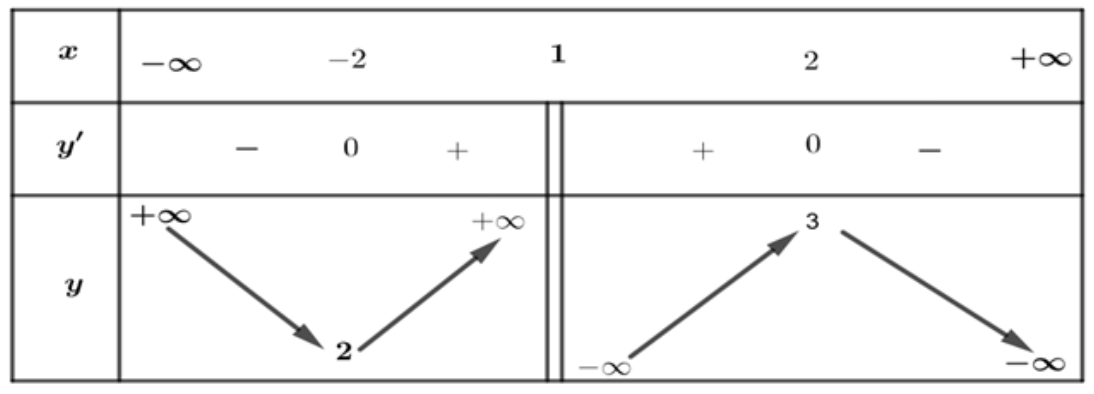
Tìm số đường TCĐ và TCN của đồ thị hàm số \[y = g\left( x \right) = \frac{1}{{2f\left( x \right) – 3}}\].
Hướng dẫn giải
Dựa vào bảng biến thiên ta có:
Phương trình \[2f\left( x \right) – 3 = 0 \Leftrightarrow f\left( x \right) = \frac{3}{2} \Leftrightarrow \left[ \begin{gathered}
x = {x_1} \in \left( {1;2} \right) \hfill \\
x = {x_2} \in \left( {2; + \infty } \right) \hfill \\
\end{gathered} \right.\]
\[\mathop {\lim }\limits_{x \to x_1^ + } g\left( x \right) = \mathop {\lim }\limits_{x \to x_1^ + } \frac{1}{{2f\left( x \right) – 3}} = + \infty \]
\[\mathop {\lim }\limits_{x \to x_1^ – } g\left( x \right) = \mathop {\lim }\limits_{x \to x_1^ – } \frac{1}{{2f\left( x \right) – 3}} = – \infty \]
\[ \Rightarrow \] Đường thẳng \[x = {x_1}\] là một TCĐ của đồ thị hàm số \[y = \frac{1}{{2f\left( x \right) – 3}}\]
\[\mathop {\lim }\limits_{x \to x_2^ + } g\left( x \right) = \mathop {\lim }\limits_{x \to x_2^ + } \frac{1}{{2f\left( x \right) – 3}} = – \infty \]
\[\mathop {\lim }\limits_{x \to x_2^ – } g\left( x \right) = \mathop {\lim }\limits_{x \to x_2^ – } \frac{1}{{2f\left( x \right) – 3}} = + \infty \]
\[ \Rightarrow \] Đường thẳng \[x = {x_2}\] là một TCĐ của đồ thị hàm số \[y = \frac{1}{{2f\left( x \right) – 3}}\]
\[\mathop {\lim }\limits_{x \to + \infty } g\left( x \right) = \mathop {\lim }\limits_{x \to + \infty } \frac{1}{{2f\left( x \right) – 3}} = 0\]
\[\mathop {\lim }\limits_{x \to – \infty } g\left( x \right) = \mathop {\lim }\limits_{x \to – \infty } \frac{1}{{2f\left( x \right) – 3}} = 0\]
\[ \Rightarrow \] Đường thẳng \[y = 0\] là một TCN của đồ thị hàm số \[y = \frac{1}{{2f\left( x \right) – 3}}\]
Vậy đồ thị hàm số \[y = \frac{1}{{2f\left( x \right) – 3}}\] có 2 đường TCĐ là \[x = {x_1}\]; \[x = {x_2}\] và 1 TCN là \[y = 0\]
Câu 2. Cho hàm số \[f\left( x \right) = a{x^3} + b{x^2} + cx + d\] \[\left( {a,b,c,d \in \mathbb{R}} \right)\] có đồ thị như hình vẽ:
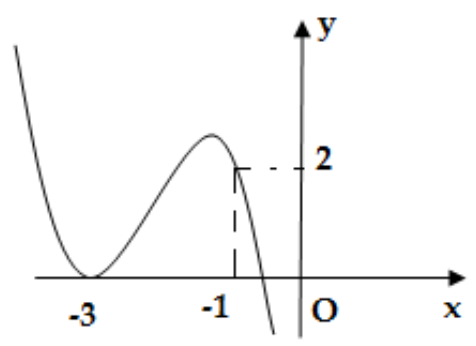
Đồ thị hàm số \[g\left( x \right) = \frac{{\left( {{x^2} + 4x + 3} \right)\sqrt {{x^2} + x} }}{{{{\left( {f\left( x \right)} \right)}^2} – 2f\left( x \right)}}\] có bao nhiêu đường TCĐ?
Hướng dẫn giải
Điều kiện \[\left\{ \begin{gathered}
\left[ \begin{gathered}
x \leqslant – 1 \hfill \\
x \geqslant 0 \hfill \\
\end{gathered} \right. \hfill \\
f\left( x \right) \ne 0 \hfill \\
f\left( x \right) \ne 2 \hfill \\
\end{gathered} \right.\]
Ta có: \[g\left( x \right) = \frac{{\left( {{x^2} + 4x + 3} \right)\sqrt {{x^2} + x} }}{{{{\left( {f\left( x \right)} \right)}^2} – 2f\left( x \right)}}\]\[ = \frac{{\left( {x + 1} \right)\left( {x + 3} \right)\sqrt {x\left( {x + 1} \right)} }}{{{{\left( {f\left( x \right)} \right)}^2} – 2f\left( x \right)}}\]
Xét phương trình \[{\left( {f\left( x \right)} \right)^2} – 2f\left( x \right) = 0 \Leftrightarrow \left[ \begin{gathered}
f\left( x \right) = 0 \hfill \\
f\left( x \right) = 2 \hfill \\
\end{gathered} \right.\]
Với \[f\left( x \right) = 0 \Leftrightarrow \left[ \begin{gathered}
x = – 3 \hfill \\
x = {x_1} \in \left( { – 1;0} \right){\text{ }}\left( {lo\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle\cdot}$}}{a} i} \right) \hfill \\
\end{gathered} \right.\] trong đó \[x = – 3\] là nghiệm kép
Nên mẫu sẽ có nhân từ \[{\left( {x + 3} \right)^2}\] do đó \[x = – 3\] là 1 tiệm cận đứng.
Với \[f\left( x \right) = 2 \Leftrightarrow \left[ \begin{gathered}
x = – 1 \hfill \\
x = {x_2} \in \left( { – 3; – 1} \right) \hfill \\
x = {x_3} \in \left( { – \infty ; – 3} \right) \hfill \\
\end{gathered} \right.\], ba nghiệm này là nghiệm đơn
Nên \[f\left( x \right) – 2 = k\left( {x + 1} \right)\left( {x – {x_2}} \right)\left( {x – {x_3}} \right)\], ta thấy trong \[{g\left( x \right)}\] thì \[\left( {x + 1} \right)\] sẽ bị rút gọn nên có thêm \[x = {x_2} \in \left( { – 3; – 1} \right)\] và \[x = {x_3} \in ( – \infty ; – 3)\] là tiệm cận đứng.
Vậy tóm lại đồ thị có 3 tiệm cận đứng là \[x = – 3\]; \[x = {x_2}\]; \[x = {x_3}\]
Câu 3. Cho đồ thị hàm đa thức bậc bốn \[y = f\left( x \right)\] như hình vẽ bên dưới.
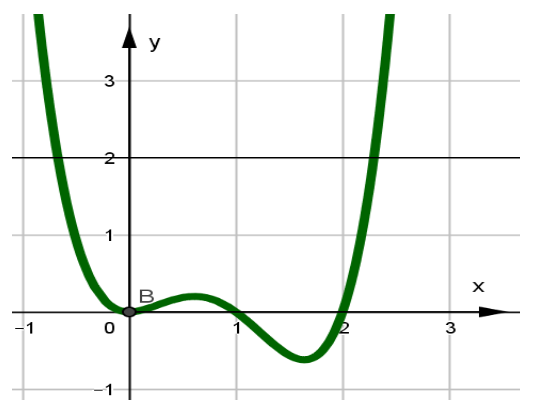
Hỏi đồ thị của hàm số \[g\left( x \right) = \frac{{\left( {{x^6} + 1} \right)\left( {{x^2} – 5x} \right)\sqrt {{x^2} – 2x} }}{{\left[ {{f^2}\left( x \right) – 2f\left( x \right)} \right]\left( {2x – 10} \right)}}\] có bao nhiêu đường TCĐ và TCN.
Hướng dẫn giải
Điều kiện: \[\left[ \begin{gathered}
x \leqslant 0 \hfill \\
x \geqslant 2 \hfill \\
\end{gathered} \right.\]
Giả sử \[f\left( x \right) = a{x^4} + b{x^3} + c{x^2} + dx + e\]
Vì \[\mathop {\lim }\limits_{x \to – \infty } g\left( x \right) = \frac{{ – 1}}{{2{a^2}}};\mathop {\lim }\limits_{x \to + \infty } g\left( x \right) = \frac{1}{{2{a^2}}}\] nên đồ thị hàm số \[{g\left( x \right)}\] có 2 TCN \[y = \pm \frac{1}{{2{a^2}}}\]
Dễ thấy \[\left[ {{f^2}\left( x \right) – 2f\left( x \right)} \right]\left( {2x – 10} \right) = 0\]\[ \Leftrightarrow f\left( x \right)\left[ {f\left( x \right) – 2} \right] \cdot 2 \cdot \left( {x – 5} \right) = 0\] có các nghiệm
\[\;x = 0;x = 1;x = 2;x = 5;x = {x_1} \in \left( { – 1;0} \right);x = {x_2} \in \left( {2;3} \right)\]
So sánh với điều kiện của căn và bội của nghiệm ta thấy đồ thị \[{g\left( x \right)}\] có các đường tiệm cận đứng là: \[x = 0;x = 2;x = {x_1};x = {x_2}\]
Vậy đồ thị hàm số \[{g\left( x \right)}\] có 6 đường tiệm cận kể cả ngang và đứng.
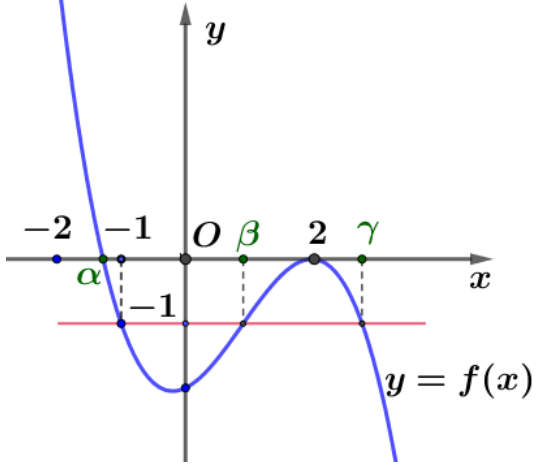
Câu 4. Cho hàm số \[y = f\left( x \right) = a{x^3} + b{x^2} + cx + d\left( {a \ne 0} \right)\] có đồ thị như hình dưới đây:
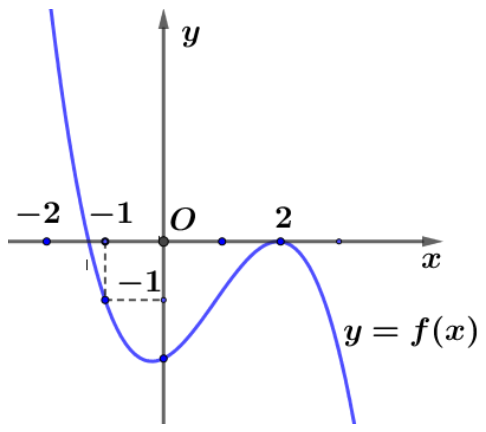
Tìm số đường tiệm cận đứng và tiệm cận ngang của đồ thị hàm số
\[y = g\left( x \right) = \frac{{\left( {{x^2} + 2x – 3} \right)\sqrt x }}{{\left( {{x^2} – x} \right)\left[ {{{\left( {f\left( x \right)} \right)}^2} + f\left( x \right)} \right]}}\]
Hướng dẫn giải
Trước hết, ta cần tìm \[x \geqslant 0\] để \[\left( {{x^2} – x} \right)\left[ {{{\left( {f\left( x \right)} \right)}^2} + f\left( x \right)} \right] = 0\]
Ta có:
\[\left( {{x^2} – x} \right)\left[ {{{\left( {f\left( x \right)} \right)}^2} + f\left( x \right)} \right] = 0 \Leftrightarrow \left[ \begin{gathered}
x = 0 \hfill \\
x = 1 \hfill \\
f\left( x \right) = 0 \hfill \\
f\left( x \right) = – 1 \hfill \\
\end{gathered} \right.\]
Từ đồ thị hàm số \[y = f\left( x \right)\] ta thấy:
\[f\left( x \right) = 0 \Leftrightarrow \left[ \begin{gathered}
x = \alpha \in \left( { – 2; – 1} \right) \hfill \\
x = 2 \hfill \\
\end{gathered} \right.\] và \[f\left( x \right) = a\left( {x – \alpha } \right){\left( {x – 2} \right)^2}\]
\[f\left( x \right) = – 1 \Leftrightarrow \left[ \begin{gathered}
x = – 1 \hfill \\
x = \beta \in \left( {0;2} \right) \hfill \\
x = \gamma \in \left( {2; + \infty } \right) \hfill \\
\end{gathered} \right.\]\[ \Rightarrow f\left( x \right) + 1 = a\left( {x + 1} \right)\left( {x – \beta } \right)\left( {x – \gamma } \right)\]
Vậy hàm số \[y = g\left( x \right)\] có tập xác định là \[D = \left( {0; + \infty } \right)\backslash \left\{ {\beta ;1;2;\gamma } \right\}\]
Khi đó ta có:
\[y = g\left( x \right) = \frac{{\left( {x – 1} \right)\left( {x + 3} \right)\sqrt x }}{{x\left( {x – 1} \right)f\left( x \right)\left[ {f\left( x \right) + 1} \right]}}\]
\[ = \frac{{x + 3}}{{\sqrt x a\left( {x – \alpha } \right){{\left( {x – 2} \right)}^2}a\left( {x + 1} \right)\left( {x – \beta } \right)\left( {x – \gamma } \right)}}\]
\[ = \frac{{x + 3}}{{{a^2}\sqrt x \left( {x + 1} \right){{\left( {x – 2} \right)}^2}\left( {x – \alpha } \right)\left( {x – \beta } \right)\left( {x – \gamma } \right)}}\]
+) Tìm TCN: Ta có: \[\mathop {\lim }\limits_{x \to + \infty } g\left( x \right) = 0\] (do bậc của tử nhỏ hơn bậc của mẫu) \[ \Rightarrow y = 0\] là TCN của đồ thị hàm số \[y = g\left( x \right)\].
+) Tìm TCĐ:
\[g\left( x \right) = \frac{{x + 3}}{{{a^2}\sqrt x \left( {x + 1} \right){{\left( {x – 2} \right)}^2}\left( {x – \alpha } \right)\left( {x – \beta } \right)\left( {x – \gamma } \right)}}\]
Mẫu thức của \[{g\left( x \right)}\] có 6 nghiệm phân biệt là \[\alpha ; – 1;0;\beta ;2;\gamma \]
* Tại \[x = \alpha \in \left( { – 2; – 1} \right)\] và \[x = – 1\] các giới hạn một bên của \[{g\left( x \right)}\] không tồn tại nên \[x = \alpha ;x = – 1\] không phải TCĐ của đồ thị hàm số \[y = g\left( x \right)\].
* Tại \[x = 0\] ta có \[\mathop {\lim }\limits_{x \to {0^ + }} g\left( x \right) = \mathop {\lim }\limits_{x \to {0^ + }} \frac{{x + 3}}{{{a^2}\sqrt x \left( {x + 1} \right){{\left( {x – 2} \right)}^2}\left( {x – \alpha } \right)\left( {x – \beta } \right)\left( {x – \gamma } \right)}} = + \infty \] nên \[x = 0\] là một TCĐ của đồ thị hàm số \[y = g\left( x \right)\]
* Tại \[x = \beta ;x = 2\] và \[x = \gamma \] các giới hạn một bên của \[{g\left( x \right)}\] đều là giới hạn vô cực (vì mẫu thức bằng \[0\] còn tử thức khác \[0\] tại các điểm đó) nên \[x = \beta ;x = 2\] và \[x = \gamma \] là các TCĐ của đồ thị hàm số \[y = g\left( x \right)\].
Vậy đồ thị hàm số \[y = g\left( x \right)\] có 1 đường TCN là \[y = 0\] và 4 đường TCĐ là \[x = 0;x = \beta ;x = 2\] và \[x = \gamma \].
Câu 5. Cho hàm số \[y = f\left( x \right)\] xác định, liên tục trên \[\mathbb{R}\] và có bảng biến thiên như sau:
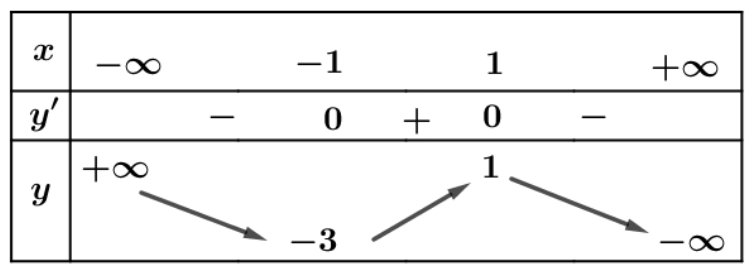
Tìm số tiệm cận ngang và số tiệm cận đứng của đồ thị hàm số \[g\left( x \right) = \frac{3}{{f\left( {{x^3} + x + 1} \right) – 1}}\].
Hướng dẫn giải
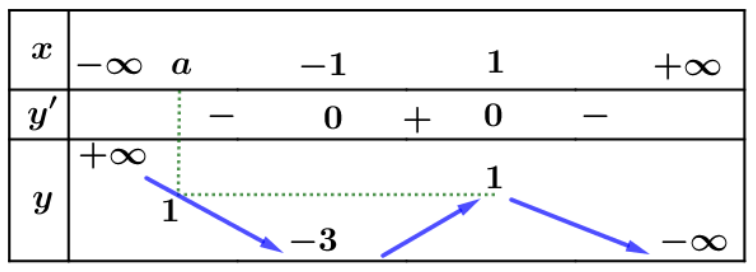
Từ bảng biến thiên ta thấy:
\[f\left( {{x^3} + x + 1} \right) – 1 = 0 \Leftrightarrow f\left( {{x^3} + x + 1} \right) = 1\]\[ \Leftrightarrow \left[ \begin{gathered}
{x^3} + x + 1 = 1 \hfill \\
{x^3} + x + 1 = a,{\text{ }}a < – 1 \hfill \\
\end{gathered} \right.\]\[ \Leftrightarrow \left[ \begin{gathered}
x = 0 \hfill \\
{x^3} + x + 1 = a,{\text{ }}a < – 1{\text{ }}\left( 2 \right) \hfill \\
\end{gathered} \right.\]
Lập bảng biến thiên của hàm số \[h\left( x \right) = {x^3} + x + 1\] ta thấy với \[a < – 1\] thì phương trình \[{x^3} + x + 1 = a\] có nghiệm duy nhất \[{x_0} < – 1\]
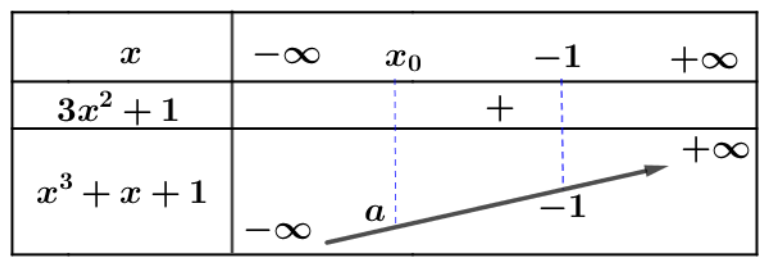
Suy ra hàm số \[y = g\left( x \right)\] có tập xác định là \[D = \mathbb{R}\backslash \left\{ {0;{x_0}} \right\},{\text{ }}{x_0} < – 1\]
+) Tìm tiệm cận ngang
Đặt \[t = {x^3} + x + 1\]. Khi \[x \to + \infty \] và khi \[x \to – \infty \] thì \[t \to – \infty \]
Do đó:
\[\mathop {\lim }\limits_{x \to + \infty } f\left( {{x^3} + x + 1} \right) = \mathop {\lim }\limits_{x \to + \infty } f\left( t \right) = – \infty \Rightarrow \mathop {\lim }\limits_{x \to + \infty } \frac{3}{{f\left( {{x^3} + x + 1} \right) – 1}} = 0\]
\[\mathop {\lim }\limits_{x \to – \infty } f\left( {{x^3} + x + 1} \right) = \mathop {\lim }\limits_{x \to – \infty } f\left( t \right) = + \infty \Rightarrow \mathop {\lim }\limits_{x \to – \infty } \frac{3}{{f\left( {{x^3} + x + 1} \right) – 1}} = 0\]
Suy ra đồ thị hàm số \[y = g\left( x \right)\] có 1 tiệm cận ngang đó là đường thẳng \[y = 0\].
+) Tìm tiệm cận đứng
![]()
\[g\left( x \right) = \frac{3}{{f\left( {{x^3} + x + 1} \right) – 1}}\]
Tại các điểm \[x = 0\];\[x = {x_0}\] mẫu của \[{g\left( x \right)}\] nhận giá trị bằng \[0\] còn tử luôn nhận giá trị bằng \[3\].
Và do hàm số xác định trên mỗi khoảng \[\left( { – \infty ;{x_0}} \right),\left( {{x_0};0} \right),\left( {0; + \infty } \right){\text{ }}\] nên giới hạn một bên của hàm số \[y = g\left( x \right)\] tại các điểm \[x = 0\];\[x = {x_0}\] là các giới hạn vô cực.
Do đó, đồ thị hàm số \[y = g\left( x \right)\] có hai tiệm cận đứng, đó là các đường thẳng \[x = 0\];\[x = {x_0}\]
Vậy đồ thị hàm số \[y = g\left( x \right)\] có 3 đường tiệm cận (1 TCN \[y = 0\] và 2 TCĐ \[x = 0\];\[x = {x_0}\])
Dạng 4. Một số bài toán về tiệm cận chứa tham số
Câu 1. Tìm các giá trị thực của tham số \[m\] để đồ thị hàm số \[y = \frac{{mx + 7}}{{mx – 1}}\] có tiệm cận đứng đi qua điểm \[A\left( {1; – 2} \right)\].
Hướng dẫn giải
Để đường tiệm cận đứng đi qua \[A\left( {1; – 2} \right)\] thì đường tiệm cận đứng phải có phương trình \[x = 1\].
Khi đó \[x = 1\] là nghiệm của \[mx – 1 = 0\]. Suy ra \[m = 1\].
Thử lại: với \[m = 1\] thì đồ thị hàm số \[y = \frac{{x + 7}}{{x – 1}}\] có đường TCĐ \[x = 1\] đi qua \[A\left( {1; – 2} \right)\].
Vậy \[m = 1\] là giá trị cần tìm.
Câu 2. Tìm các tham số m để đồ thị hàm số \[y = \frac{{x – 1}}{{{x^2} + mx + 4}}\] có đúng hai đường tiệm cận?
Hướng dẫn giải
Ta có: \[\mathop {\lim }\limits_{x \to \pm \infty } y = \mathop {\lim }\limits_{x \to \pm \infty } \frac{\begin{gathered}
\hfill \\
\frac{1}{x} – \frac{1}{{{x^2}}} \hfill \\
\end{gathered} }{\begin{gathered}
1 + \frac{m}{x} + \frac{4}{{{x^2}}} \hfill \\
\hfill \\
\end{gathered} } = 0\]
Nên đồ thị hàm số luôn có một đường tiệm cận ngang là \[y = 0\].
Do đó để đồ thị hàm số có hai đường tiệm cận thì đồ thị hàm số cần có đúng một đường tiệm cận đứng. Hay phương trình \[f\left( x \right) = {x^2} + mx + 4 = 0\] có nghiệm kép hoặc có hai nghiệm phân biệt trong đó có \[1\] nghiệm bằng \[1\].
Ta có: \[\Delta = {m^2} – 4 \cdot 1 \cdot 4 = {m^2} – 16\]
Khi đó: \[\left[ \begin{gathered}
{m^2} – 16 = 0 \hfill \\
\left\{ \begin{gathered}
{m^2} – 16 > 0 \hfill \\
f\left( 1 \right) = 0 \hfill \\
\end{gathered} \right. \hfill \\
\end{gathered} \right. \Leftrightarrow \left[ \begin{gathered}
m = 4 \hfill \\
m = – 4 \hfill \\
\left\{ \begin{gathered}
{m^2} – 16 > 0 \hfill \\
m = – 5 \hfill \\
\end{gathered} \right. \hfill \\
\end{gathered} \right. \Leftrightarrow \left[ \begin{gathered}
m = 4 \hfill \\
m = – 4 \hfill \\
m = – 5 \hfill \\
\end{gathered} \right.\]
Vậy \[m \in \left\{ { – 4;4; – 5} \right\}\]
Câu 3. Cho hàm số \[y = \frac{{2mx + m}}{{x – 1}}\]. Với giá trị nào của \[m\] thì đường tiệm cận đứng, tiệm cận ngang của đồ thị hàm số cùng với hai trục toạ độ tạo thành một hình chữ nhật có diện tích là \[8\]?
Hướng dẫn giải
Để đồ thị hàm số tồn tại tiệm cận đứng thì \[ad – bc \ne 0 \Leftrightarrow – 3m \ne 0 \Leftrightarrow m \ne 0\]
Khi đó tiệm cận đứng, tiệm cận ngang của đồ thị lần lượt là các đường thẳng \[x = 1\] và \[y = 2m\].
Khi đó diện tích hình chữ nhật tạo thành là: \[\left| {1.2m} \right| = 8 \Leftrightarrow \left| m \right| = 4 \Leftrightarrow m = \pm 4\]
Câu 4. Biết đồ thị \[\left( C \right)\] của hàm số \[y = \frac{{ax + b}}{{cx + d}}\] đi qua điểm \[A\left( { – 1;7} \right)\] và giao điểm hai tiệm cận của \[\left( C \right)\] là điểm \[I\left( { – 2;3} \right)\]. Biết \[c\] là số nguyên dương và \[a,c\] là các số nguyên tố cùng nhau. Tìm các số \[a,b,c,d\].
Hướng dẫn giải
Đồ thị \[\left( C \right)\] có tiệm cận đứng là \[x = – \frac{d}{c}\] và tiệm cận ngang là \[y = \frac{a}{c}\] với điều kiện \[ad – bc \ne 0\]
Khi đó ta có:
\[\left\{ \begin{gathered}
– \frac{d}{c} = – 2\begin{array}{*{20}{c}}
{} \\
{}
\end{array} \hfill \\
\frac{a}{c} = 3\begin{array}{*{20}{c}}
{} \\
{}
\end{array} \hfill \\
\end{gathered} \right.\]\[ \Leftrightarrow \left\{ \begin{gathered}
d = 2c \hfill \\
a = 3c \hfill \\
\end{gathered} \right.\xrightarrow[{c \in {\mathbb{N}^*}}]{{\left( {a,c} \right) = 1}}c = 1\]\[ \Rightarrow \left\{ \begin{gathered}
d = 2 \hfill \\
a = 3 \hfill \\
\end{gathered} \right.\]\[ \Rightarrow \left( C \right):y = \frac{{3x + b}}{{x + 2}}\]
Do \[A\left( { – 1;7} \right) \in \left( C \right) \Rightarrow 7 = \frac{{ – 3 + b}}{{ – 1 + 2}} \Leftrightarrow b = 10\]
Câu 5. Cho hàm số \[y = \frac{{2x + m}}{{x – m}}\]. Tìm tất cả các giá trị của \[m\] để đồ thị hàm số có 2 đường tiệm cận cùng với hai trục toạ độ tạo thành một hình vuông.
Hướng dẫn giải
Ta có đường tiệm cận ngang của đồ thị hàm số là \[y = 2\].
Với \[2 \cdot m – 1 \cdot m \ne 0 \Leftrightarrow m \ne 0\] thì đường tiệm cận đứng của đồ thị hàm số là \[x = m\].
Để 2 đường tiệm cận cùng với 2 trục toạ độ tạo thành một hình vuông thì \[\left| m \right| = 2 \Leftrightarrow m = \pm 2\]
Câu 6. Tính tổng bình phương tất cả các giá trị của m để đồ thị hàm số \[y = \sqrt {2{x^2} – 3x + 5} + mx – 6\] có tiệm cận ngang.
Hướng dẫn giải
Có \[\mathop {\lim }\limits_{x \to + \infty } y = \mathop {\lim }\limits_{x \to + \infty } \left[ {\sqrt {2{x^2} – 3x + 5} – \sqrt 2 x + \left( {m + \sqrt 2 } \right)x – 6} \right]\]
\[ = \mathop {\lim }\limits_{x \to + \infty } \left[ {\frac{{ – 3x + 5}}{{\sqrt {2{x^2} – 3x + 5} + \sqrt 2 x}} – 6 + \left( {m + \sqrt 2 } \right)x} \right]\]
Vậy đồ thị hàm số có tiệm cận ngang khi \[x \to + \infty \Leftrightarrow m + \sqrt 2 = 0 \Leftrightarrow m = – \sqrt 2 \]
(do \[\mathop {\lim }\limits_{x \to + \infty } \left( {\frac{{ – 3x + 5}}{{\sqrt {2{x^2} – 3x + 5} + \sqrt 2 x}} – 6} \right) = \frac{{ – 3}}{{2\sqrt 2 }} – 6\] hữu hạn)
Có \[\mathop {\lim }\limits_{x \to – \infty } y = \mathop {\lim }\limits_{x \to – \infty } \left[ {\sqrt {2{x^2} – 3x + 5} + \sqrt 2 x + \left( {m – \sqrt 2 } \right)x – 6} \right]\]
\[ = \mathop {\lim }\limits_{x \to – \infty } \left[ {\frac{{ – 3x + 5}}{{\sqrt {2{x^2} – 3x + 5} – \sqrt 2 x}} – 6 + \left( {m – \sqrt 2 } \right)x} \right]\]
Vậy đồ thị hàm số có tiệm cận ngang khi \[x \to – \infty \Leftrightarrow m – \sqrt 2 = 0 \Leftrightarrow m = \sqrt 2 \]
(do \[\mathop {\lim }\limits_{x \to + \infty } \left( {\frac{{ – 3x + 5}}{{\sqrt {2{x^2} – 3x + 5} – \sqrt 2 x}} – 6} \right) = \frac{3}{{2\sqrt 2 }} – 6\] hữu hạn)
Vậy tổng bình phương tất cả các giá trị của m thoả mãn bằng \[{\left( { – \sqrt 2 } \right)^2} + {\left( {\sqrt 2 } \right)^2} = 4\].