Sơ đồ bài toán khảo sát và vẽ đồ thị hàm số
Bước 1. Tìm tập xác định của hàm số
Bước 2. Tính đạo hàm \[y’ = f’\left( x \right)\]
Bước 3. Tìm nghiệm của phương trình \[f’\left( x \right) = 0\]
Bước 4. Tính giới hạn \[\mathop {\lim }\limits_{x \to + \infty } y;\mathop {\lim }\limits_{x \to – \infty } y\] và tìm tiệm cận đứng, ngang (nếu có)
Bước 5. Lập bảng biến thiên
Bước 6. Kết luận tính biến thiên và cực trị (nếu có)
Bước 7. Tìm các điểm đặc biệt của đồ thị (giao với trục \[Ox\], \[Oy\], các điểm đối xứng,…)
Bước 8. Vẽ đồ thị
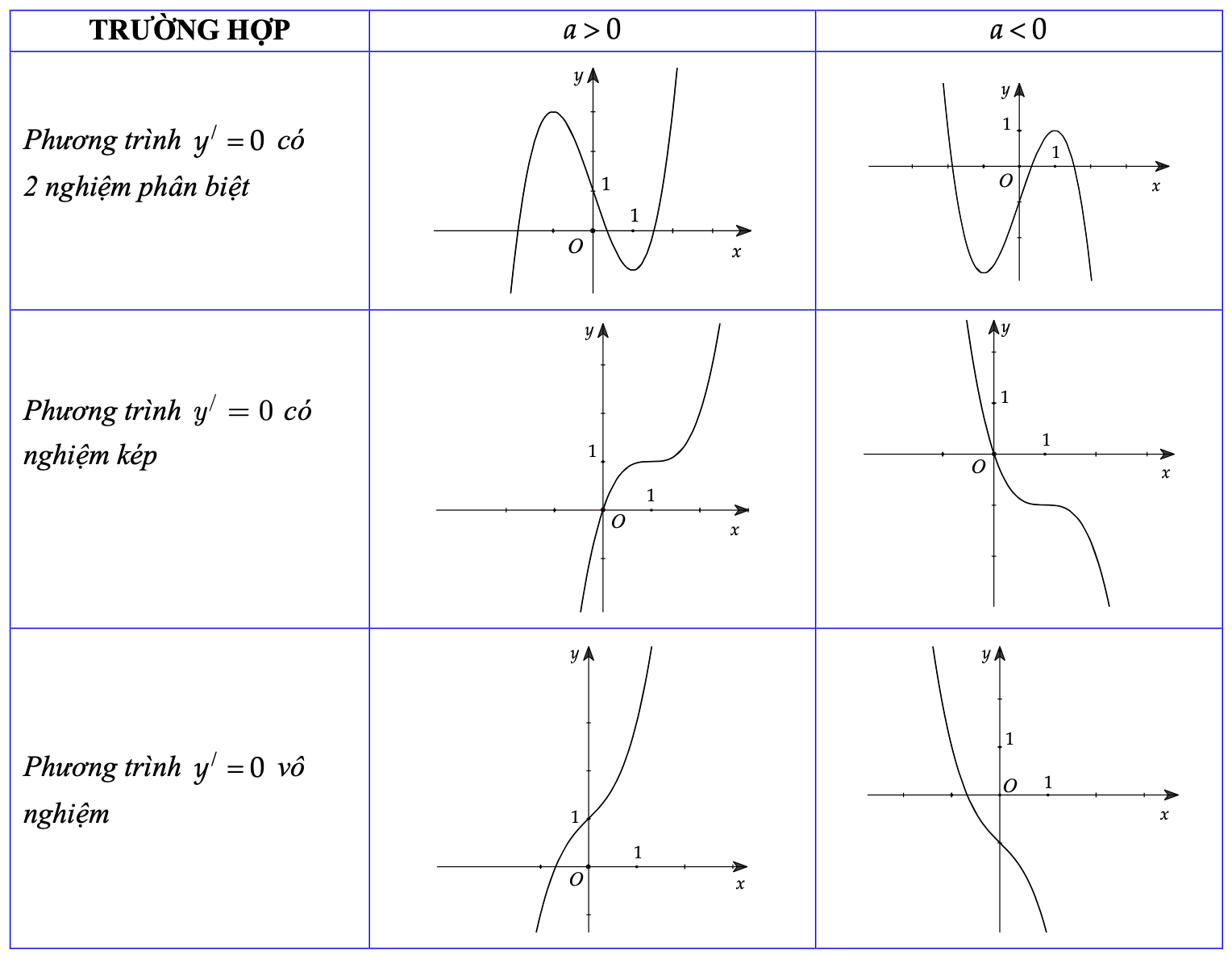
Các dạng đồ thị của các hàm số thường gặp
Hàm số bậc ba \[y = a{x^3} + b{x^2} + cx + d\left( {a \ne 0} \right)\]
Câu 1. Khảo sát và vẽ đồ thị hàm số \[y = {x^3} – 3{x^2} + 2\].
Hướng dẫn giải
TXĐ: \[D = \mathbb{R}\]
Sự biến thiên
+) Chiều biến thiên:
\[y’ = 3{x^2} – 6x\]. Xét \[y’ = 0 \Leftrightarrow \left[ \begin{gathered}
x = 0 \hfill \\
x = 2 \hfill \\
\end{gathered} \right.\]
+) Các giới hạn tại vô cực
\[\mathop {\lim }\limits_{x \to + \infty } y = \mathop {\lim }\limits_{x \to + \infty } {x^3}\left( {1 – \frac{3}{x} + \frac{2}{{{x^3}}}} \right) = + \infty \]
\[\mathop {\lim }\limits_{x \to – \infty } y = \mathop {\lim }\limits_{x \to – \infty } {x^3}\left( {1 – \frac{3}{x} + \frac{2}{{{x^3}}}} \right) = – \infty \]
+) Bảng biến thiên
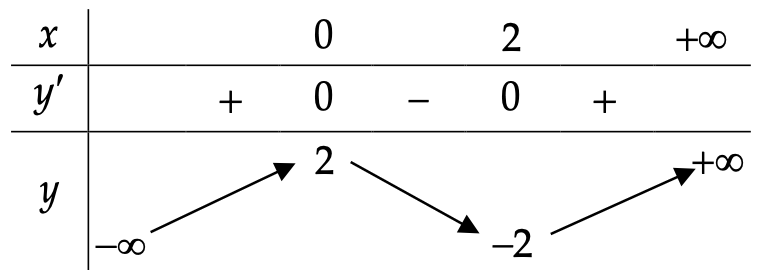
Hàm số đồng biến trên các khoảng \[\left( { – \infty ;0} \right)\] và \[\left( {2; + \infty } \right)\]
Hàm số nghịch biến trên khoảng \[\left( {0;2} \right)\]
+) Cực trị:
Hàm số đạt cực đại tại \[x = 0;{y_{C\rlap{–} D}} = y\left( 0 \right) = 2\]. Hàm số đạt cực tiểu tại \[x = 2;{y_{CT}} = y\left( 2 \right) = – 2\]
+) Đồ thị:
Ta có: \[{x^3} – 3{x^2} + 2 = 0 \Leftrightarrow \left[ \begin{gathered}
x = 1 \hfill \\
{x^2} – 2x – 2 = 0 \hfill \\
\end{gathered} \right.\]
\[ \Rightarrow \] Đồ thị hàm số qua điểm \[A\left( {1;0} \right)\]
Cho \[x = 0 \Rightarrow y = 2\]: Đồ thị hàm số cắt \[Oy\] tại B\[\left( {0;2} \right)\]
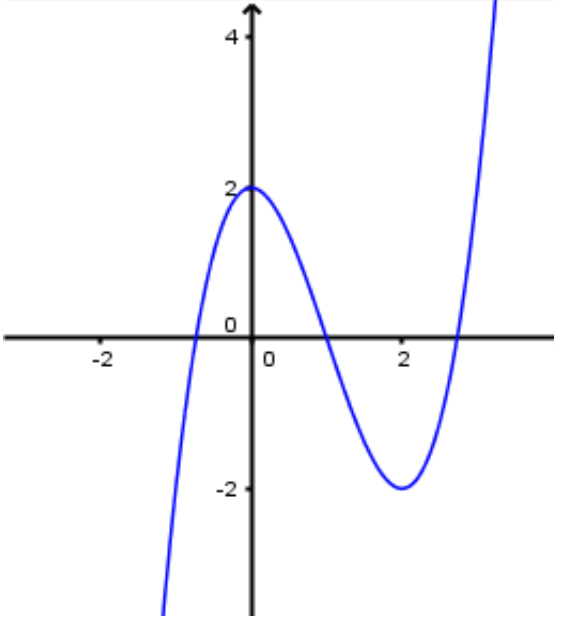
Lưu ý: Đồ thị hàm số nhận điểm \[I\left( {1;0} \right)\] làm tâm đối xứng. Hoành độ điểm \[I\] là nghiệm của phương trình \[y” = 0\] (điểm uốn).
Câu 2. Khảo sát và vẽ đồ thị hàm số \[y = {x^3} + 1\].
Hướng dẫn giải
TXĐ: \[D = \mathbb{R}\]
Sự biến thiên
+) Chiều biến thiên:
\[y’ = 3{x^2} \geqslant 0,\forall x \in \mathbb{R}\]. Xét \[y’ = 0 \Leftrightarrow x = 0\]
Suy ra hàm số luôn đồng biến trên khoảng \[\left( { – \infty ; + \infty } \right)\]
+) Cực trị: Hàm số không có cực trị
+) Các giới hạn tại vô cực
\[\mathop {\lim }\limits_{x \to + \infty } y = \mathop {\lim }\limits_{x \to + \infty } {x^3} = + \infty \]
\[\mathop {\lim }\limits_{x \to – \infty } y = \mathop {\lim }\limits_{x \to – \infty } {x^3} = – \infty \]
+) Bảng biến thiên
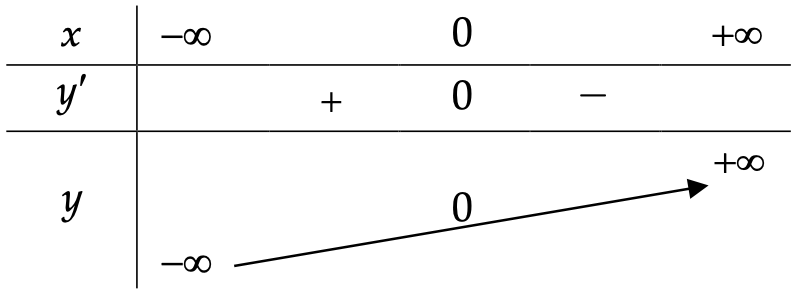
+) Đồ thị:
Ta có: \[{x^3} = 0 \Leftrightarrow x = 0\]. Vậy đồ thị hàm số qua \[O\left( {0;0} \right)\]
Cho \[x = 1 \Rightarrow y = 1\]: Đồ thị hàm số cắt \[Oy\] tại \[B\left( {1;1} \right)\]
Cho \[x = – 1 \Rightarrow y = – 1\]: Đồ thị hàm số cắt qua \[C\left( { – 1; – 1} \right)\]
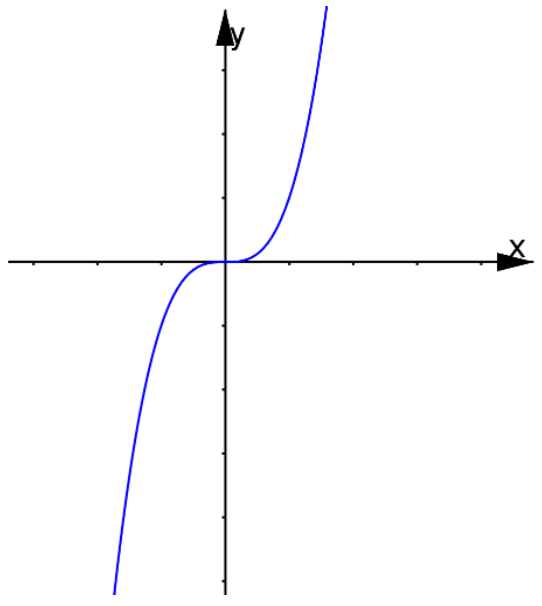
Lưu ý: Đồ thị hàm số nhận điểm \[O\left( {0;0} \right)\] làm tâm đối xứng. Hoành độ điểm \[O\] là nghiệm của phương trình \[y” = 0\] (điểm uốn).
Hàm số trùng phương \[y = a{x^4} + b{x^2} + c\left( {a \ne 0} \right)\]
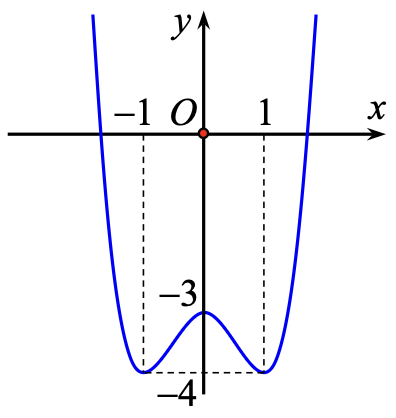
Câu 1. Khảo sát và vẽ đồ thị hàm số \[y = {x^4} – 2{x^2} – 3\]
Hướng dẫn giải
TXĐ: \[D = \mathbb{R}\]
Sự biến thiên
+) Chiều biến thiên:
\[y’ = 4{x^3} – 4x = 4x\left( {{x^2} – 1} \right)\]. Xét \[y’ = 0 \Leftrightarrow \left[ \begin{gathered}
x = 0 \hfill \\
x = \pm 1 \hfill \\
\end{gathered} \right.\]
+) Các giới hạn tại vô cực
\[\mathop {\lim }\limits_{x \to + \infty } y = \mathop {\lim }\limits_{x \to \pm \infty } {x^4}\left( {1 – \frac{2}{{{x^2}}} – \frac{3}{{{x^4}}}} \right) = + \infty \]
+) Bảng biến thiên
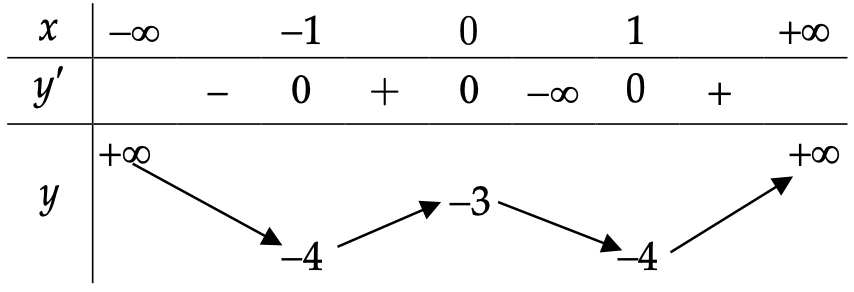
Hàm số đồng biến trên các khoảng \[\left( { – 1;0} \right)\] và \[\left( {1; + \infty } \right)\]
Hàm số nghịch biến trên các khoảng \[\left( { – \infty ; – 1} \right)\] và \[\left( {0;1} \right)\]
+) Cực trị:
Hàm số đạt cực đại tại \[x = 0;{y_{C\rlap{–} D}} = y\left( 0 \right) = – 3\]
Hàm số đạt cực tiểu tại \[x = \pm 1;{y_{C\rlap{–} D}} = y\left( { \pm 1} \right) = – 4\]
+) Đồ thị:
Ta có: \[{x^4} – 2{x^2} – 3 = 0 \Leftrightarrow x = \pm 1\]. Vậy đồ thị hàm số qua \[A\left( {1;0} \right),B\left( { – 1;0} \right)\]
Cho \[x = 0 \Rightarrow y = – 3\]. Đồ thị hàm số cắt \[Oy\] tại \[C\left( {0; – 3} \right)\].
Cho \[x = \pm 2 \Rightarrow y = 5\]. Đồ thị hàm số qua \[D\left( { – 2;5} \right),E\left( {2;5} \right)\].
Lưu ý: Đồ thị hàm số nhận được \[Oy\] làm trục đối xứng.
Câu 2. Khảo sát và vẽ đồ thị hàm số \[y = 4 – \frac{{{x^2}}}{2} – \frac{{{x^4}}}{8}\]
Hướng dẫn giải
TXĐ: \[D = \mathbb{R}\]
Sự biến thiên
+) Chiều biến thiên:
\[y’ = – x – \frac{{{x^3}}}{2} = – x\left( {1 + \frac{{{x^2}}}{2}} \right)\]. Xét \[y’ = 0 \Leftrightarrow x = 0\]
+) Các giới hạn tại vô cực
\[\mathop {\lim }\limits_{x \to + \infty } y = \mathop {\lim }\limits_{x \to \pm \infty } {x^4}\left( { – 1 – \frac{1}{{2{x^2}}} – \frac{1}{{8{x^4}}}} \right) = – \infty \]
+) Bảng biến thiên
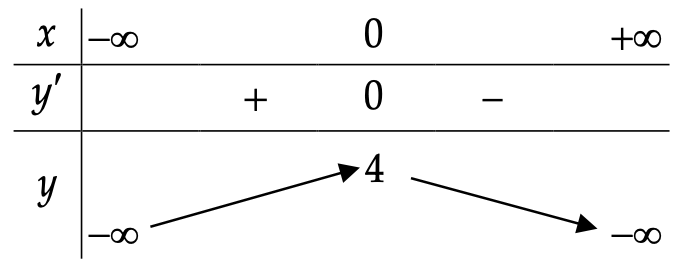
Hàm số đồng biến trên các khoảng \[\left( { – \infty ;0} \right)\]
Hàm số nghịch biến trên các khoảng \[\left( {0; + \infty } \right)\]
+) Cực trị:
Hàm số đạt cực đại tại \[x = 0;{y_{C\rlap{–} D}} = y\left( 0 \right) = – 3\]
Hàm số không có cực tiểu
+) Đồ thị:
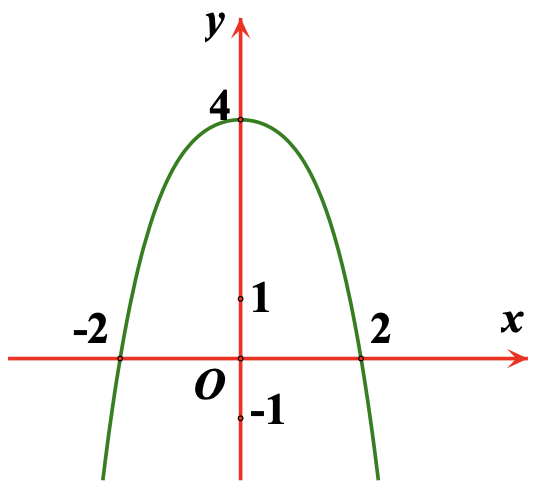
Cho \[x = \pm 2 \Rightarrow y = 0\]. Đồ thị hàm số qua \[C\left( { – 2;0} \right),D\left( {2;0} \right)\].
Lưu ý: Đồ thị hàm số nhận \[Oy\] làm trục đối xứng.
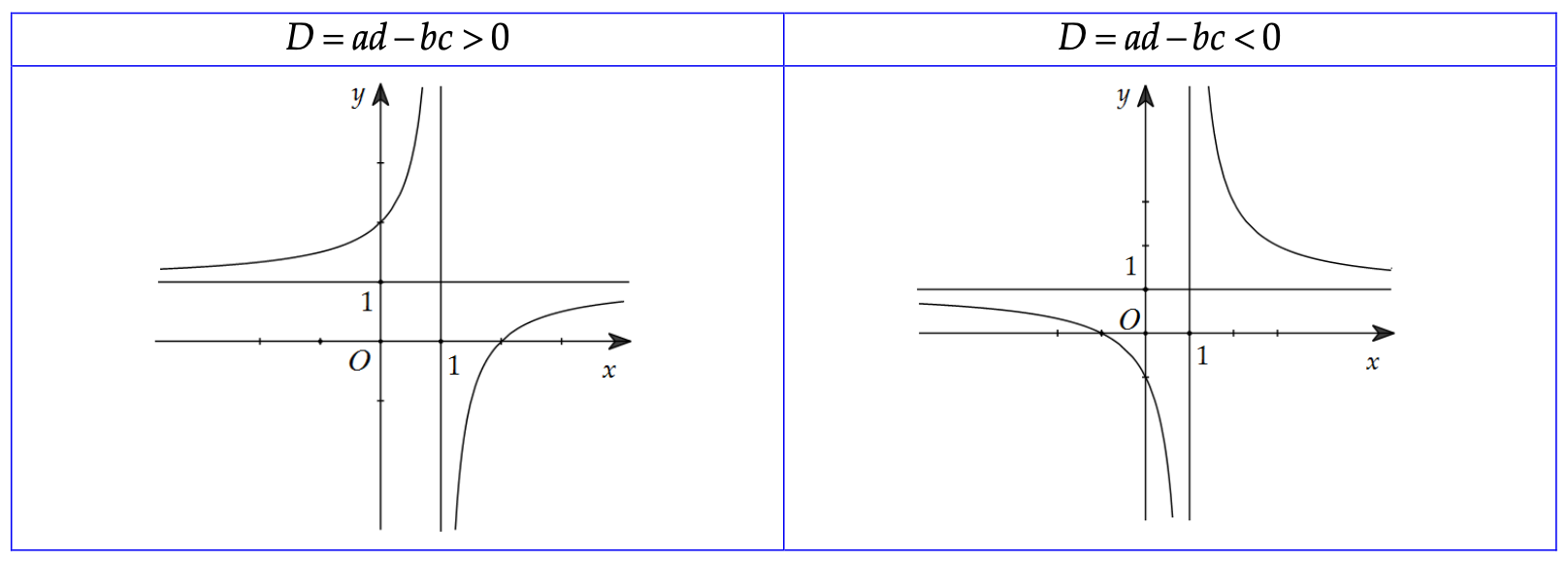
Hàm số nhất biến \[y = \frac{{ax + b}}{{cx + d}}\left( {c \ne 0,ad – bc \ne 0} \right)\]
Câu 1. Khảo sát và vẽ đồ thị hàm số \[\frac{{x + 1}}{{x – 1}}\]
Hướng dẫn giải
TXĐ: \[D = \mathbb{R}\backslash \left\{ 1 \right\}\]
Sự biến thiên
+) Chiều biến thiên:
\[y’ = \frac{{ – 2}}{{{{\left( {x – 1} \right)}^2}}}\]
Ta thấy \[{y’}\] không xác định khi \[x = 1\]; \[{y’}\] luôn âm với mọi \[x \ne 1\]
Vậy hàm số nghịch biến trên các khoảng \[\left( {1; + \infty } \right)\] và \[\left( { – \infty ;1} \right)\]
+) Cực trị:
Hàm số không có cực trị
+) Tiệm cận:
\[\mathop {\lim }\limits_{x \to \pm \infty } y = \lim \frac{{x + 1}}{{x – 1}} = 1\]. Vậy đường thẳng \[y = 1\] là tiệm cận ngang.
\[\mathop {\lim }\limits_{x \to {1^ + }} y = \mathop {\lim }\limits_{x \to {1^ + }} \frac{{x + 1}}{{x – 1}} = + \infty \]. Vậy đường thẳng \[x = 1\] là tiệm cận đứng.
+) Bảng biến thiên
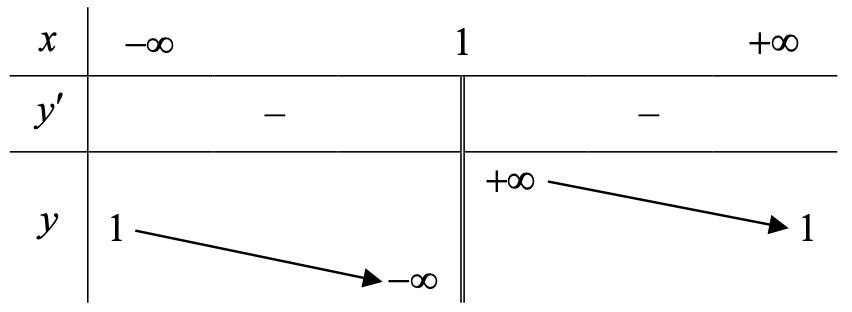
+) Đồ thị:
Đồ thị cắt trục tung tại điểm \[A\left( {0; – 1} \right)\] và cắt trục hoành tại điểm \[B\left( { – 1;0} \right)\]
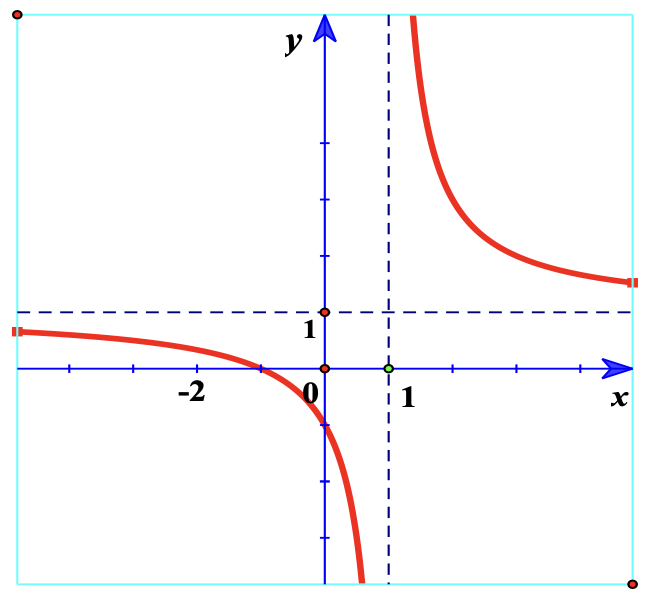
Lưu ý: Giao điểm \[I\left( {1;1} \right)\] của hai tiệm cận là tâm đối xứng của đồ thị.
Câu 2. Khảo sát và vẽ đồ thị của hàm số \[y = \frac{{x + 1}}{{2x – 1}}\]
Hướng dẫn giải
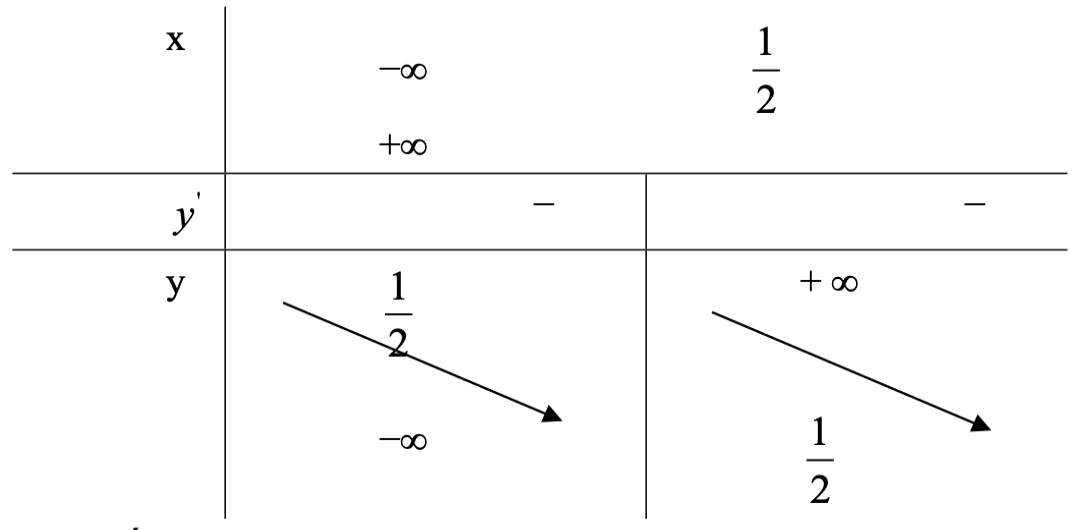
TXĐ: \[D = \mathbb{R}\backslash \left\{ {\frac{1}{2}} \right\}\]
Ta có: \[y’ = \frac{{ – 3}}{{{{\left( {2x – 1} \right)}^2}}} < 0\] với mọi \[x \ne \frac{1}{2}\]
\[\mathop {\lim }\limits_{x \to + \infty } y = \mathop {\lim }\limits_{x \to – \infty } y = \frac{1}{2}\]. Đồ thị hàm số có tiệm cận ngang là \[y = \frac{1}{2}\]
\[\mathop {\lim }\limits_{x \to {{\left( {\frac{1}{2}} \right)}^ + }} y = + \infty ,\mathop {\lim }\limits_{x \to {{\left( {\frac{1}{2}} \right)}^ – }} y = – \infty \]. Đồ thị hàm số có tiệm cận đứng là \[x = \frac{1}{2}\]
+) Bảng biến thiên của hàm số có dạng:
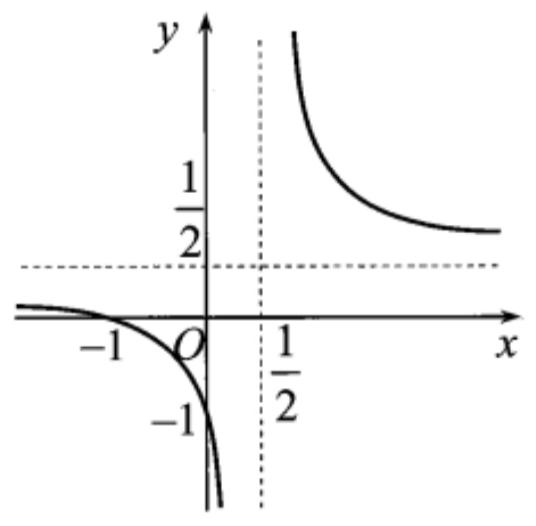
+) Đồ thị hàm số có dạng:
Một số phép biến đổi đồ thị
Cho hàm số \[y = f\left( x \right)\] có đồ thị \[\left( C \right)\] với số \[a > 0\] ta có:
☞ Hàm số \[y = f\left( x \right) + a\] có đồ thị \[\left( {C’} \right)\] là tịnh tiến \[\left( C \right)\] theo phương của \[Oy\] lên trên \[a\] đơn vị.
☞ Hàm số \[y = f\left( x \right) – a\] có đồ thị \[\left( {C’} \right)\] là tịnh tiến \[\left( C \right)\] theo phương của \[Oy\] xuống dưới \[a\] đơn vị.
☞ Hàm số \[y = f\left( {x + a} \right)\] có đồ thị \[\left( {C’} \right)\] là tịnh tiến \[\left( C \right)\] theo phương của \[Ox\] qua trái \[a\] đơn vị.
☞ Hàm số \[y = f\left( {x – a} \right)\] có đồ thị \[\left( {C’} \right)\] là tịnh tiến \[\left( C \right)\] theo phương của \[Ox\] qua phải \[a\] đơn vị.
☞ Hàm số \[y = – f\left( x \right)\] có đồ thị \[\left( {C’} \right)\] là đối xứng của \[\left( C \right)\] qua trục \[Ox\].
☞ Hàm số \[y = f\left( { – x} \right)\] có đồ thị \[\left( {C’} \right)\] là đối xứng của \[\left( C \right)\] qua trục \[Oy\].
☞ Từ đồ thị \[\left( C \right):y = f\left( x \right)\] suy ra đồ thị \[\left( {C’} \right):y = f\left( {\left| x \right|} \right)\]
Ta có: \[y = f\left( {\left| x \right|} \right) = \left\{ \begin{gathered}
f\left( x \right){\text{ }}khi{\text{ }}x \geqslant 0 \hfill \\
f\left( { – x} \right){\text{ }}khi{\text{ }}x < 0 \hfill \\
\end{gathered} \right.\] và \[y = f\left( {\left| x \right|} \right)\] là hàm chẵn nên đồ thị \[\left( {C’} \right)\] nhận \[Oy\] làm trục đối xứng.
* Cách vẽ \[\left( {C’} \right)\] từ \[\left( C \right)\]:
+) Giữ nguyên phần đồ thị bên phải \[Oy\] của đồ thị \[\left( C \right):y = f\left( x \right)\]
+) Bỏ phần đồ thị bên trái \[Oy\] của \[\left( C \right)\], lấy đối xứng phần đồ thị được giữ qua \[Oy\].
Ví dụ. Từ đồ thị \[\left( C \right):y = f\left( x \right) = {x^3} – 3x\] suy ra đồ thị \[\left( {C’} \right):y = {\left| x \right|^3} – 3\left| x \right|\].
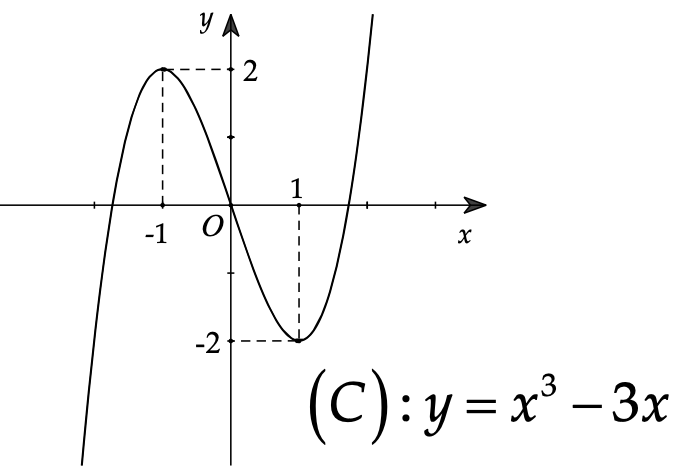
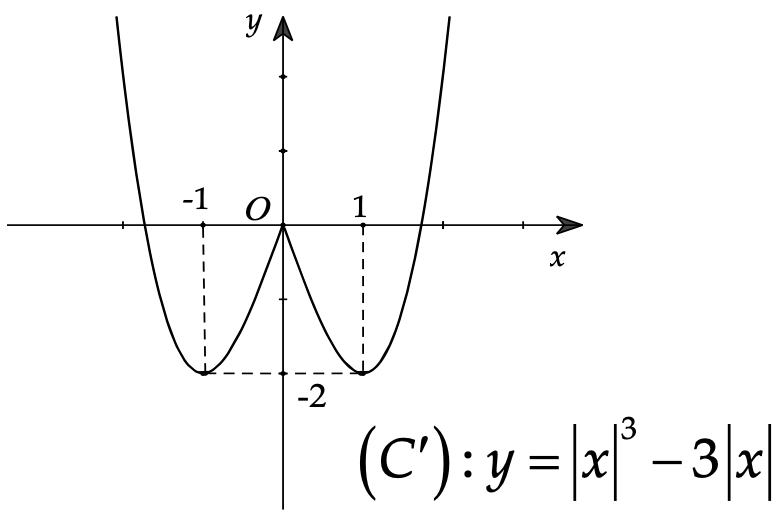
Ta có: \[y = {\left| x \right|^3} – 3\left| x \right| = \left\{ \begin{gathered}
{x^3} – 3x{\text{ }}khi{\text{ }}x \geqslant 0 \hfill \\
– {x^3} + 3x = – \left( {{x^3} – 3x} \right){\text{ }}khi{\text{ }}x < 0 \hfill \\
\end{gathered} \right.\]
Cách vẽ đồ thị \[\left( {C’} \right)\]
+) Bỏ phần đồ thị của \[\left( C \right)\] bên trái \[Oy\], giữ nguyên \[\left( C \right)\] bên phải \[Oy\].
+) Lấy đối xứng phần đồ thị được giữ qua \[Oy\].
☞ Từ đồ thị \[\left( C \right):y = f\left( x \right)\] suy ra đồ thị \[\left( {C’} \right):y = \left| {f\left( x \right)} \right|\]
Ta có: \[y = \left| {f\left( x \right)} \right| = \left\{ \begin{gathered}
f\left( x \right){\text{ }}khi{\text{ }}x \geqslant 0 \hfill \\
– f\left( x \right){\text{ }}khi{\text{ }}x < 0 \hfill \\
\end{gathered} \right.\]
* Cách vẽ \[\left( {C’} \right)\] từ \[\left( C \right)\]:
+) Giữ nguyên phần đồ thị phía trên \[Ox\] của đồ thị \[\left( C \right):y = f\left( x \right)\]
+) Bỏ phần đồ thị phía dưới \[Ox\] của \[\left( C \right)\], lấy đối xứng phần đồ thị bị bỏ qua \[Ox\].
Ví dụ. Từ đồ thị \[\left( C \right):y = f\left( x \right) = {x^3} – 3x\] suy ra đồ thị \[\left( {C’} \right):y = \left| {{x^3} – 3x} \right|\].
Cách vẽ đồ thị \[\left( {C’} \right)\]
+) Bỏ phần đồ thị của \[\left( C \right)\] phía dưới \[Ox\], giữ nguyên \[\left( C \right)\] phía trên \[Ox\].
+) Lấy đối xứng phần đồ thị bị bỏ qua \[Ox\].

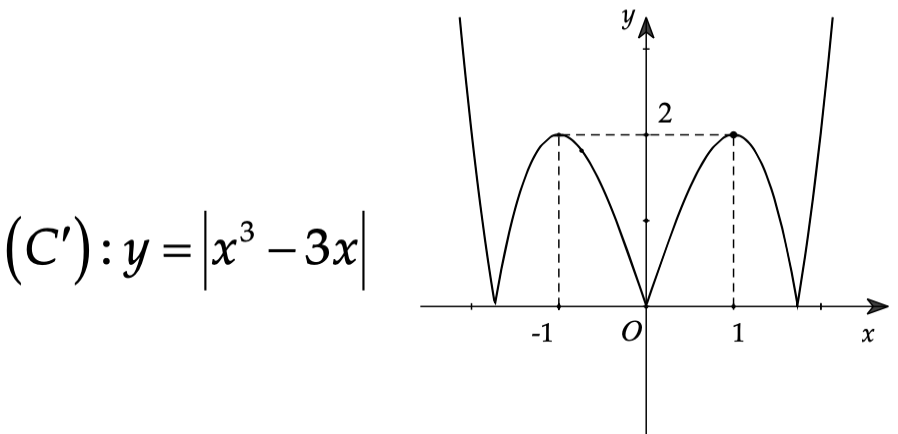
Chú ý: Với dạng \[y = \left| {f\left( {\left| x \right|} \right)} \right|\] ta lần lượt biến đổi 2 đồ thị \[y = f\left( {\left| x \right|} \right)\] và \[y = \left| {f\left( x \right)} \right|\]
Ví dụ. Từ đồ thị \[\left( C \right):y = f\left( x \right) = {x^3} – 3x\] suy ra đồ thị \[y = \left| {{{\left| x \right|}^3} – 3\left| x \right|} \right|\]
Biến đổi \[\left( C \right)\] để được đồ thị \[\left( {C’} \right):y = {\left| x \right|^3} – 3\left| x \right|\]
Biến đổi \[\left( {C’} \right):y = {\left| x \right|^3} – 3\left| x \right|\] ta được đồ thị \[\left( {C”} \right):y = \left| {{{\left| x \right|}^3} – 3\left| x \right|} \right|\]
☞ Từ đồ thị \[\left( C \right):y = u\left( x \right) \cdot v\left( x \right)\] suy ra đồ thị \[\left( {C’} \right):y = \left| {u\left( x \right)} \right| \cdot v\left( x \right)\]
Ta có: \[y = \left| {u\left( x \right)} \right| \cdot v\left( x \right) = \left\{ \begin{gathered}
u\left( x \right) \cdot v\left( x \right) = f\left( x \right){\text{ }}khi{\text{ }}u\left( x \right) \geqslant 0 \hfill \\
– u\left( x \right) \cdot v\left( x \right) = f\left( x \right){\text{ }}khi{\text{ }}u\left( x \right) < 0 \hfill \\
\end{gathered} \right.\]
* Cách vẽ \[\left( {C’} \right)\] từ \[\left( C \right)\]:
+) Giữ nguyên phần đồ thị trên miền \[u\left( x \right) \geqslant 0\] của đồ thị \[\left( C \right):y = f\left( x \right)\]
+) Bỏ phần đồ thị trên miền \[u\left( x \right) < 0\] của \[\left( C \right)\], lấy đối xứng phần đồ thị bị bỏ qua \[Ox\].
Ví dụ.
a) Từ đồ thị \[\left( C \right):y = f\left( x \right) = 2{x^3} – 3{x^2} + 1\] suy ra đồ thị \[\left( {C’} \right):y = \left| {x – 1} \right|\left( {2{x^2} – x – 1} \right)\]
Ta có: \[y = \left| {x – 1} \right|\left( {2{x^2} – x – 1} \right) = \left\{ \begin{gathered}
f\left( x \right){\text{ }}khi{\text{ }}x \geqslant 1 \hfill \\
– f\left( x \right){\text{ }}khi{\text{ }}x < 1 \hfill \\
\end{gathered} \right.\]
Đồ thị \[\left( {C’} \right)\]:
+) Giữ nguyên \[\left( C \right)\] với \[x \geqslant 1\].
+) Bỏ \[\left( C \right)\] với \[x < 1\]. Lấy đối xứng phần đồ thị bị bỏ qua \[Ox\].
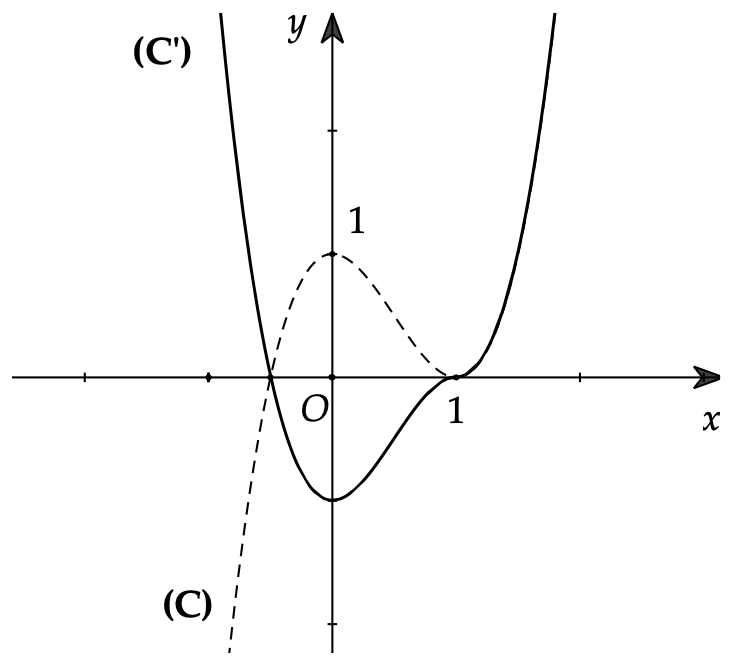
Nhận xét: Trong quá trình thực hiện phép suy đồ thị nên lấy đối xứng các điểm đặc biệt của \[\left( C \right)\]: giao điểm với \[Ox\], \[Oy\], \[C\rlap{–} D\], \[CT\]…
b) Từ đồ thị \[\left( C \right):y = f\left( x \right) = \frac{x}{{x – 1}}\] suy ra đồ thị \[y = \frac{x}{{\left| {x – 1} \right|}}\]
Ta có: \[y = \frac{x}{{\left| {x – 1} \right|}} = \left\{ \begin{gathered}
\frac{x}{{x – 1}}{\text{ }}khi{\text{ }}x \in \left( {1; + \infty } \right)\begin{array}{*{20}{c}}
{} \\
{}
\end{array} \hfill \\
– \frac{x}{{x – 1}}{\text{ }}khi{\text{ }}x \in \left( { – \infty ;1} \right)\begin{array}{*{20}{c}}
{} \\
{}
\end{array} \hfill \\
\end{gathered} \right.\]
Đồ thị \[\left( {C’} \right)\]:
+) Bỏ phần đồ thị của \[\left( C \right)\] với \[x < 1\], giữ nguyên \[\left( C \right)\] với \[x > 1\]
+) Lấy đối xứng phần đồ thị bị bỏ qua \[Ox\].
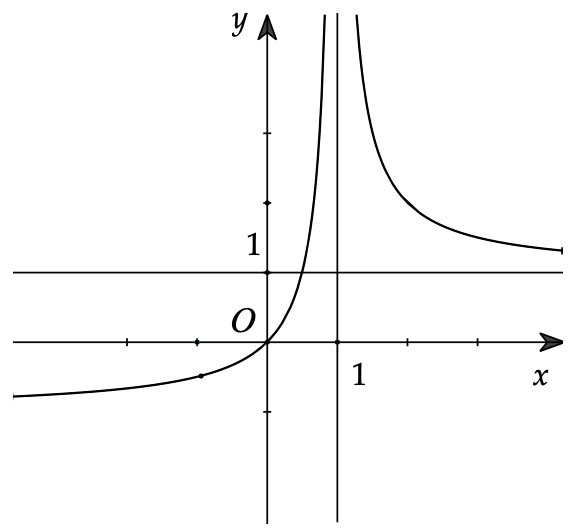
Nhận xét: Đối với hàm phân thức thì nên lấy đối xứng các đường tiệm cận để thực hiện phép suy đồ thị một cách tương đối chính xác.