Tính đơn điệu của hàm số

Tính đơn điệu của hàm số

Lý thuyết

Định nghĩa

Cho hàm số \[y = f\left( x \right)\] xác định trên K với K là một khoảng.

+) Hàm số \[y = f\left( x \right)\] được gọi là đồng biến (tăng) trên K nếu

\[\forall {x_1},{x_2} \in K,{x_1} < {x_2} \Rightarrow f\left( {{x_1}} \right) < f\left( {{x_2}} \right)\]

+) Hàm số \[y = f\left( x \right)\] được gọi là nghịch biến (giảm) trên K nếu

\[\forall {x_1},{x_2} \in K,{x_1} < {x_2} \Rightarrow f\left( {{x_1}} \right) > f\left( {{x_2}} \right)\]

+) Hàm số đồng biến hoặc nghịch biến trên K được gọi chung là đơn điệu trên K.

Định lý

Cho hàm số \[y = f\left( x \right)\] có đạo hàm trên khoảng K.

+) Nếu \[f’\left( x \right) \geqslant 0,\forall x \in K\] và \[f’\left( x \right) = 0\] xảy ra tại một số hữu hạn điểm trên K thì hàm số \[y = f\left( x \right)\] đồng biến trên khoảng K.

+) Nếu \[f’\left( x \right) \leqslant 0,\forall x \in K\] và \[f’\left( x \right) = 0\] xảy ra tại một số hữu hạn điểm trên K thì hàm số \[y = f\left( x \right)\] nghịch biến trên khoảng K.

Lưu ý:

+) Nếu hàm số \[y = f\left( x \right)\] liên tục trên đoạn \[\left[ {a;b} \right]\] và \[f’\left( x \right) > 0,{\text{ }}\forall x \in \left( {a;{\text{ }}b} \right)\] thì ta nói hàm số đồng biến trên đoạn \[\left[ {a;b} \right]\]

+) Nếu hàm số \[y = f\left( x \right)\] liên tục trên đoạn \[\left[ {a;b} \right]\] và \[f’\left( x \right) < 0,{\text{ }}\forall x \in \left( {a;{\text{ }}b} \right)\] thì ta nói hàm số nghịch biến trên đoạn \[\left[ {a;b} \right]\]

+) Tương tự với các khái niệm hàm số đồng biến, nghịch biến trên các nửa khoảng.

Phương pháp xét tính đơn điệu của hàm số

Xét tính đơn điệu của hàm số \[y = f\left( x \right)\] trên tập xác định

Bước 1: Tìm tập xác định D

Bước 2: Tính đạo hàm \[y’ = f’\left( x \right)\]

Bước 3: Tìm nghiệm của \[f’\left( x \right)\] hoặc những giá trị x làm cho \[f’\left( x \right)\] không xác định

Bước 4: Lập bảng biến thiên

Bước 5: Kết luận

Chú ý: Đối với bài toán trắc nghiệm, ta có thể sử dụng Phương pháp sử dụng MTCT.

+) Cách 1: Sử dụng chức năng lập bảng giá trị MODE 7 của máy tính Casio. Quan sát bảng kết quả nhận được về tính tăng, giảm giá trị của \[f\left( x \right)\] và dự đoán.

+) Cách 2: Tính đạo hàm, thiết lập bất phương trình đạo hàm. Sử dụng tính năng giải bất phương trình INEQ của máy tính Casio (đối với bất phương trình bậc hai, bậc ba).

Bài tập tự luận

Dạng 1. Xét tính đơn điệu của hàm số cho bởi biểu thức

Câu 1. Tìm các khoảng đồng biến, nghịch biến của hàm số \[y = {x^3}–3{x^2} + 1\]

Hướng dẫn giải

TXĐ: \[D = \mathbb{R}\]

Ta có: \[y’ = 3{x^2}–6x\]

\[y’ = 0 \Leftrightarrow 3{x^2}–6x = 0 \Leftrightarrow \left[ \begin{gathered} x = 0 \hfill \\ x{\text{ }} = {\text{ }}2 \hfill \\ \end{gathered} \right.\]

Bảng biến thiên

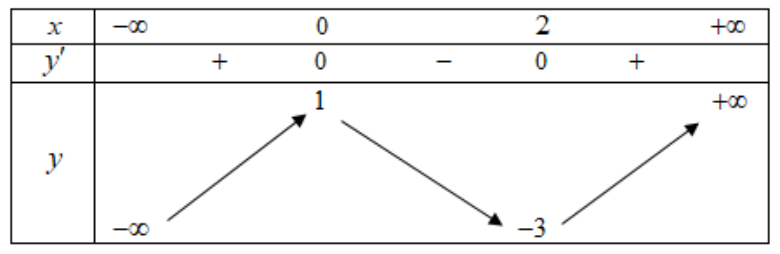
Vậy hàm số đồng biến trên các khoảng \[\left( { – \infty ;0} \right)\] và \[\left( {2; + \infty } \right)\], nghịch biến trên khoảng \[\left( {0;2} \right)\]

Câu 2. Tìm các khoảng đồng biến, nghịch biến của hàm số \[y = \frac{1}{3}{x^3} + 4x + 1\]

Hướng dẫn giải

TXĐ: \[D = \mathbb{R}\]

Ta có: \[y’ = {x^2} + 4 > 0,\forall x \in \mathbb{R}\]

Vậy hàm số đồng biến trên khoảng \[\left( { – \infty ; + \infty } \right)\]

Câu 3. Tìm các khoảng đồng biến, nghịch biến của hàm số \[y =  – \frac{1}{3}{x^3} + 5{x^2} – 26x – 1\]

Hướng dẫn giải

TXĐ: \[D = \mathbb{R}\]

Ta có: \[y’ = – {x^2} + 10x–26 = – {\left( {x–5} \right)^2}–1 < 0,\forall x \in \mathbb{R}\]

Vậy hàm số nghịch biến trên khoảng \[\left( { – \infty ; + \infty } \right)\]

Câu 4. Tìm các khoảng đồng biến, nghịch biến của hàm số \[y = \frac{1}{3}{x^3} + 3{x^2} + 9x – 1\]

Hướng dẫn giải

TXĐ: \[D = \mathbb{R}\]

Ta có: \[y’ = {x^2} + 6x + 9 = {\left( {x + 3} \right)^2} \geqslant 0,\forall x \in \mathbb{R}\]

\[y’ = 0 \Leftrightarrow x = – 3\]

Vậy hàm số đồng biến trên khoảng \[\left( { – \infty ; + \infty } \right)\]

Câu 5. Tìm các khoảng đơn điệu của hàm số \[y = {x^4}–2{x^2}\]

Hướng dẫn giải

TXĐ: \[D = \mathbb{R}\]

Ta có: \[y’ = 4{x^3}–4x = 4x\left( {{x^2}–1} \right)\]

\[y’ = 0 \Leftrightarrow \left[ \begin{gathered} x = 0{\text{ }} \hfill \\ x = \pm 1 \hfill \\ \end{gathered} \right.\]

Bảng biến thiên

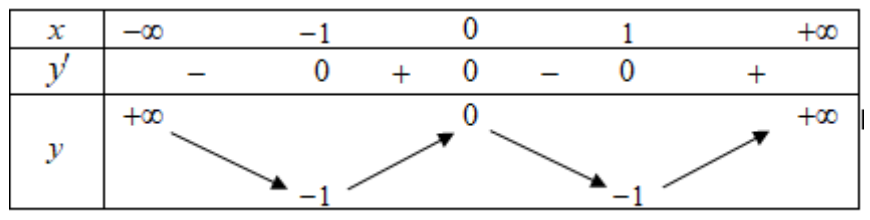
Vậy hàm số đồng biến trên khoảng \[\left( { – 1;0} \right)\] và \[\left( {1; + \infty } \right)\], nghịch biến trên các khoảng \[\left( { – \infty ; – 1} \right)\] và \[\left( {0;1} \right)\]

Dạng 2. Xét tính đơn điệu của hàm hợp cho bởi bảng biến thiên hoặc đồ thị của hàm số \[y = f\left( x \right)\] hoặc \[y = f’\left( x \right)\]

Câu 1. Cho hàm số \[y = f\left( x \right)\] xác định và liên tục trên \[\mathbb{R}\] và có bảng biến thiên

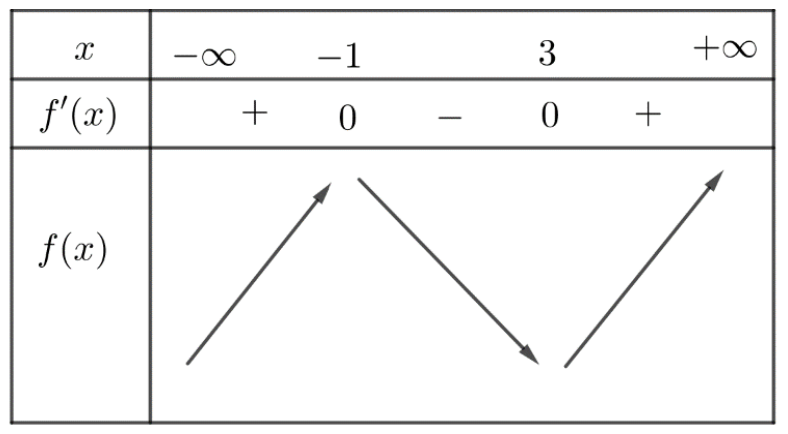
Tìm các khoảng đồng biến của hàm số \[y = f\left( {2x + 1} \right)\]

Hướng dẫn giải

Đặt \[g\left( x \right) = f\left( {2x + 1} \right)\]. Ta có: \[g’\left( x \right) = 2 \cdot f’\left( {2x + 1} \right)\]

Bảng biến thiên

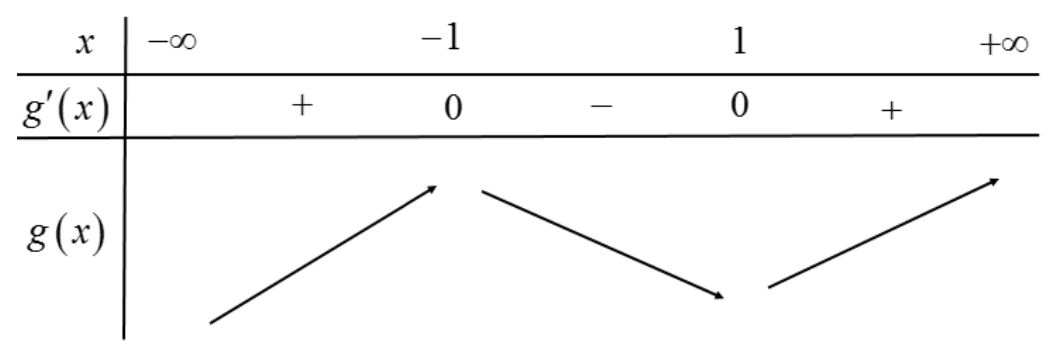
Vậy hàm số \[f\left( {2x + 1} \right)\] đồng biến trên các khoảng \[\left( { – \infty ; – 1} \right)\] và \[\left( {1; + \infty } \right)\]

Câu 2. Cho hàm số \[y = f\left( x \right)\] có bảng biến thiên

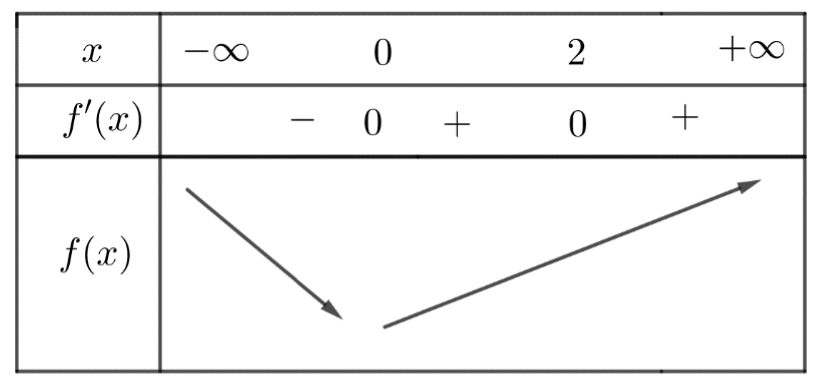
Tìm các khoảng nghịch biến của hàm số \[y = f\left( { – 2x + 6} \right)\]

Hướng dẫn giải

Đặt \[g\left( x \right) = f\left( { – 2x + 6} \right)\]. Ta có: \[g’\left( x \right) = – 2 \cdot f’\left( { – 2x + 6} \right)\]

\[g’\left( x \right) = 0 \Leftrightarrow f’\left( { – 2x + 6} \right) = 0 \Leftrightarrow \left[ \begin{gathered}
– 2x + 6 = 0 \hfill \\
– 2x + 6 = 2 \hfill \\
\end{gathered} \right. \Leftrightarrow \left[ \begin{gathered}
x = 3 \hfill \\
x = 2 \hfill \\
\end{gathered} \right.\]

Bảng biến thiên

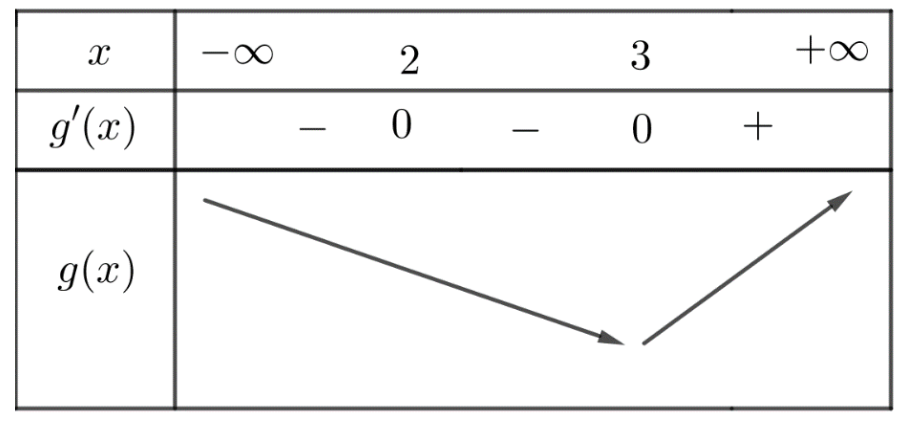
Vậy hàm số \[y = f\left( { – 2x + 6} \right)\] nghịch biến trên khoảng \[\left( { – \infty ;3} \right)\]

Câu 3. Cho hàm số \[y = f\left( x \right)\] có đạo hàm liên tục trên. Hàm số \[y = f’\left( x \right)\] có đồ thị như hình vẽ sau:

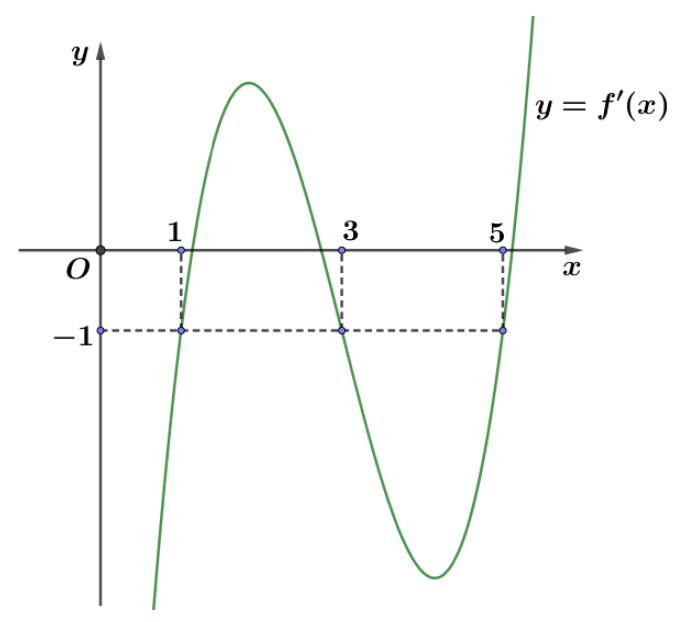
Tìm các khoảng đơn điệu của hàm số g(x) = \[f\left( x \right)\] + x + 1

Hướng dẫn giải

Ta có: g’(x) = \[f’\left( x \right)\] + 1

Dựa vào đồ thị \[y = f’\left( x \right)\] ta có:

\[f’\left( x \right) + 1 > 0 \Leftrightarrow f’\left( x \right) > – 1 \Leftrightarrow \left[ \begin{gathered}
1 < x < 3 \hfill \\
x > 5 \hfill \\
\end{gathered} \right.\]

\[f’\left( x \right) + 1 < 0 \Leftrightarrow f’\left( x \right) < – 1 \Leftrightarrow \left[ \begin{gathered}
x < 1 \hfill \\
3 < x < 5 \hfill \\
\end{gathered} \right.\]

Vậy hàm số \[g\left( x \right) = f\left( x \right) + x + 1\] đồng biến trên các khoảng \[\left( {1;3} \right)\] và \[\left( {5; + \infty } \right)\], nghịch biến trên các khoảng \[\left( { – \infty ;1} \right)\] và \[\left( {3;5} \right)\]

Câu 4. Cho hàm số \[y = f\left( x \right)\] có bảng biến thiên

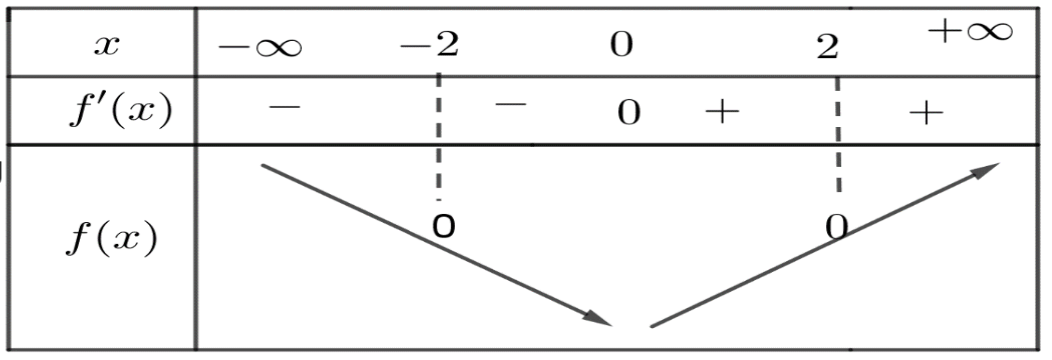
Hỏi hàm số \[y = f\left( {f\left( x \right)} \right)\] đồng biến trên những khoảng nào?

Hướng dẫn giải

Đặt \[g\left( x \right) = f\left( {f\left( x \right)} \right)\]. Ta có: \[g’\left( x \right) = f’\left( x \right) \cdot f’\left( {f\left( x \right)} \right)\]

\[g’\left( x \right) = 0 \Leftrightarrow \left[ \begin{gathered}
f’\left( x \right) = 0 \hfill \\
f’\left( {f\left( x \right)} \right) = 0 \hfill \\
\end{gathered} \right. \Leftrightarrow \left[ \begin{gathered}
x = 0 \hfill \\
f\left( x \right) = 0 \hfill \\
\end{gathered} \right. \Leftrightarrow \left[ \begin{gathered}
x = 0 \hfill \\
x = \pm 2 \hfill \\
\end{gathered} \right.\]

Xét \[f’\left( {f\left( x \right)} \right) > 0 \Leftrightarrow f\left( x \right) > 0 \Leftrightarrow \left[ \begin{gathered}
x > 2 \hfill \\
x < – 2 \hfill \\
\end{gathered} \right.\]

Bảng xét dấu:

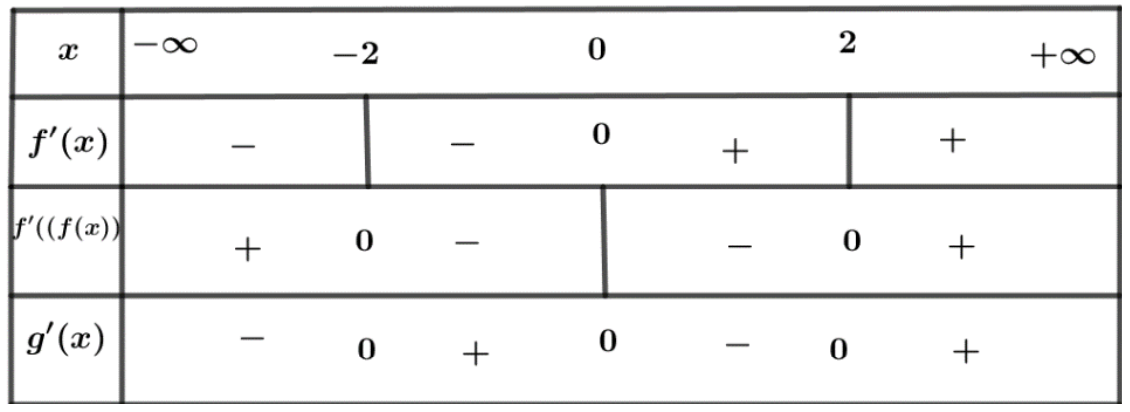
Vậy hàm số đồng biến trên mỗi khoảng \[\left( { – 2;0} \right)\] và \[\left( {2; + \infty } \right)\]

Câu 5. Cho hàm số \[y = f\left( x \right)\] liên tục trên \[\mathbb{R}\] và có bảng xét dấu đạo hàm như sau:

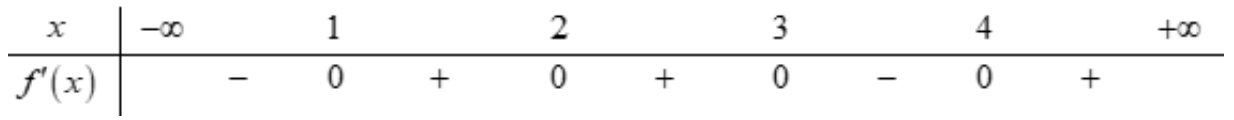
Biết \[1 < f\left( x \right) < 3,\forall x \in \mathbb{R}\]. Hàm số \[y = g\left( x \right) = f\left( {f\left( x \right)} \right) + {x^3} – 6{x^2} – 1\] có ít nhất bao nhiêu khoảng đồng biến?

Hướng dẫn giải

Ta có: \[g’\left( x \right) = f’\left( x \right) \cdot f’\left( {f\left( x \right)} \right) + 3{x^2} – 12x\]

Dựa vào bảng xét dấu \[f’\left( x \right)\] đề bài cho, vì \[1 < f\left( x \right) < 3,\forall x \in \mathbb{R} \Rightarrow f’\left( {f\left( x \right)} \right) \geqslant 0,\forall x \in \mathbb{R}\]

Bảng xét dấu \[y’ = g’\left( x \right)\]:

Vậy hàm số có ít nhất một khoảng đồng biến

Câu 6. Cho hàm số \[y = f\left( x \right)\] có đạo hàm liên tục trên \[\mathbb{R}\] và có đồ thị hàm số \[y = f’\left( x \right)\] như hình vẽ.

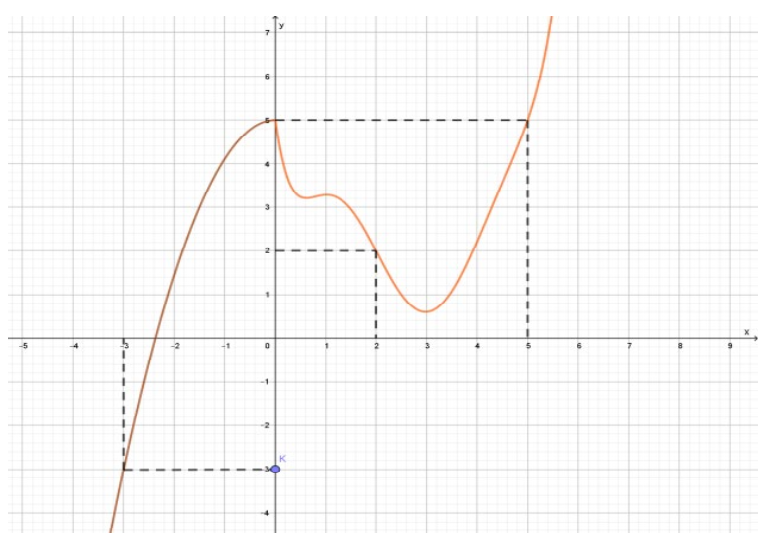
Tìm các khoảng đồng biến của hàm số \[y = g\left( x \right) = f\left( { – 2x + 1} \right) + \left( {x + 1} \right)\left( { – 2x + 4} \right)\]

Hướng dẫn giải

\[{ + ){\text{ }}g\left( x \right) = f\left( { – 2x + 1} \right) + \left( {x + 1} \right)\left( { – 2x + 4} \right) = f\left( { – 2x + 1} \right) + \left( { – 2{x^2} + 2x + 4} \right)}\]

\[{ \Rightarrow g’\left( x \right) = – 2f’\left( { – 2x + 1} \right)–4x + 2 = – 2\left[ {f’\left( { – 2x + 1} \right) + 2x–1} \right]}\]

\[{ + ){\text{ }}g’\left( x \right) > 0 \Leftrightarrow f’\left( { – 2x + 1} \right) + 2x–1 < 0 \Leftrightarrow {\text{ }}f’\left( { – 2x + 1} \right) < – 2x + 1{\text{ }}\left( 1 \right)}\]

Đặt \[t = – 2x + 1\] thì (1) trở thành \[f’\left( t \right) < t\]

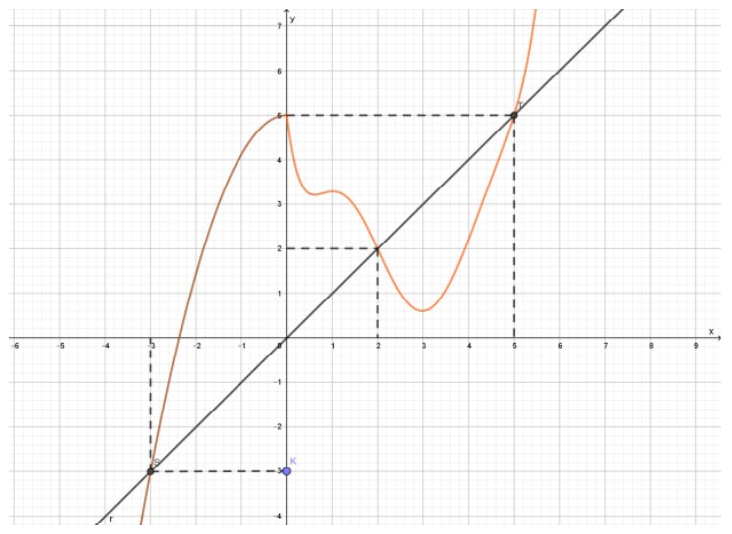
Quan sát đồ thị hàm số \[y = f’\left( t \right)\] và \[y = t\] trên cùng một hệ trục toạ độ như hình vẽ, ta thấy với \[t \in \left( { – \infty ; – 3} \right)\] và \[t \in \left( {2;5} \right)\] thì đồ thị hàm số \[y = f’\left( t \right)\] luôn nằm phía dưới đường thẳng \[y = t\].

Suy ra:

\[f’\left( t \right) < t \Leftrightarrow \left[ \begin{gathered}
t < – 3 \hfill \\
2 < t < 5 \hfill \\
\end{gathered} \right.\]

Như vậy:

\[f’\left( { – 2x + 1} \right) < – 2x + 1 \Leftrightarrow \left[ \begin{gathered}
– 2x + 1 < – 3 \hfill \\
2 < – 2x + 1 < 5 \hfill \\
\end{gathered} \right. \Leftrightarrow \left[ \begin{gathered}
x > 2 \hfill \\
– 2 < x < – \frac{1}{2}\begin{array}{*{20}{c}}
{} \\
{}
\end{array} \hfill \\
\end{gathered} \right.\]

Vậy hàm số \[y = g\left( x \right) = f\left( { – 2x + 1} \right) + \left( {x + 1} \right)\left( { – 2x + 4} \right)\] đồng biến trên khoảng \[\left( {2; + \infty } \right)\] và \[\left( { – 2; – \frac{1}{2}} \right)\]

Dạng 3. Xét tính đơn điệu của hàm số bằng phương pháp đổi biến số

Phương pháp

Xét tính đơn điệu của hàm số \[y = f\left( {u\left( x \right)} \right)\]

+) Tìm tập xác định D.

+) Đổi biến \[t = u\left( x \right)\]. Tìm điều kiện cần và đủ của t, giả sử \[t \in K\].

+) Tìm khoảng đơn điệu của hàm số \[f\left( t \right)\] trên K.

+) Kết luận khoảng đơn điệu của hàm số \[y = f\left( {u\left( x \right)} \right)\].

Chú ý:

+) Nếu hàm số \[t = u\left( x \right)\] đồng biến trên khoảng \[\left( {\alpha ;\beta } \right)\], ta có:

• Hàm số \[y = f\left( {u\left( x \right)} \right)\] đồng biến trên khoảng \[\left( {\alpha ;\beta } \right)\] ⇔ Hàm số \[y = f\left( t \right)\] đồng biến trên khoảng \[\left( {u\left( \alpha \right);u\left( \beta \right)} \right)\].
• Hàm số \[y = f\left( {u\left( x \right)} \right)\] nghịch biến trên khoảng \[\left( {\alpha ;\beta } \right)\] ⇔ Hàm số \[y = f\left( t \right)\] nghịch biến trên khoảng \[\left( {u\left( \alpha \right);u\left( \beta \right)} \right)\].

+) Nếu hàm số \[t = u\left( x \right)\] nghịch biến trên khoảng \[\left( {\alpha ;\beta } \right)\], ta có:

• Hàm số \[y = f\left( {u\left( x \right)} \right)\] đồng biến trên khoảng \[\left( {\alpha ;\beta } \right)\] ⇔ Hàm số \[y = f\left( t \right)\] nghịch biến trên khoảng \[\left( {u\left( \alpha \right);u\left( \beta \right)} \right)\].
• Hàm số \[y = f\left( {u\left( x \right)} \right)\] nghịch biến trên khoảng \[\left( {\alpha ;\beta } \right)\] ⇔ Hàm số \[y = f\left( t \right)\] đồng biến trên khoảng \[\left( {u\left( \alpha \right);u\left( \beta \right)} \right)\].

Câu 1. Xét tính đơn điệu của hàm số \[y = {x^2} – 6x + 6\sqrt {2x + 1}  – 1\]

Hướng dẫn giải

TXĐ: \[\left[ { – \frac{1}{2}; + \infty } \right)\]

Đặt \[t = \sqrt {2x + 1} \left( {t \in \left[ {0; + \infty } \right)} \right) \Rightarrow x = \frac{{{t^2} – 1}}{2}\]

Xét hàm số

\[y = {\left( {\frac{{{t^2} – 1}}{2}} \right)^2} – 6{\left( {\frac{{{t^2} – 1}}{2}} \right)^2} + 6t – 1\] \[ = \frac{1}{4}\left( {{t^4} – 14{t^2} + 24t + 9} \right)\]

\[y’ = {t^3} – 7t + 6\]

\[y’ = 0 \Leftrightarrow \left[ \begin{gathered}
t = 1 \hfill \\
t = 2 \hfill \\
t = – 3{\text{ }}\left( {lo\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle\cdot}$}}{a} i} \right) \hfill \\
\end{gathered} \right.\]

Với \[\left[ \begin{gathered}
t = 1 \Rightarrow x = 0 \hfill \\
t = 2 \Rightarrow x = \frac{3}{2} \hfill \\
\end{gathered} \right.\]

Ta có bảng dấu của \[{y’}\]

Dễ thấy hàm số \[y = \sqrt {2x + 1} \] đồng biến trên khoảng \[\left( { – \frac{1}{2}; + \infty } \right)\]

Vậy hàm số \[y = {x^2} – 6x + 6\sqrt {2x + 1}  – 1\] đồng biến trên các khoảng \[\left( { – \frac{1}{2};0} \right),\left( {\frac{3}{2}; + \infty } \right)\] và nghịch biến trên khoảng \[\left( {0;\frac{3}{2}} \right)\].

Dạng 4. Tìm điều kiện của tham số m để hàm số đồng biến, nghịch biến trên một miền

Câu 1. Tìm các giá trị của tham số m để hàm số đồng biến trên \[\mathbb{R}\].

a) \[y = {x^3} + 3{x^2} + mx + my = {x^3} + 3{x^2} + mx + m\]

b) \[y = m{x^3}–\left( {2m + 1} \right){x^2} + \left( {m + 2} \right)x–2\]

Hướng dẫn giải

a) TXĐ: \[D = \mathbb{R}\]

Ta có: \[y’ = 3{x^2} + 6x + m\]

Hàm số đồng biến trên \[\mathbb{R}\] \[ \Leftrightarrow y’ \geqslant 0,\forall x \in \mathbb{R}\]

\[ \Leftrightarrow \Delta’ \leqslant 0{\text{ }}\left( {{\text{do }}a = 3 > 0} \right)\]

\[ \Leftrightarrow 9 – 3m \leqslant 0\]

\[ \Leftrightarrow m \geqslant 3\]

Vậy \[m \geqslant 3\] thì hàm số luôn đồng biến trên \[\mathbb{R}\].

b) TXĐ: \[D = \mathbb{R}\]

+) Với \[m = 0\], hàm số trở thành \[y = – {x^2} + 2x–2\]. Suy ra hàm số đồng biến trên khoảng \[\left( { – \infty ;1} \right)\].

Vậy \[m = 0\] không thoả mãn.

+) Với \[m \ne 0\], ta có: \[y’ = 3m{x^2} – 2\left( {2m + 1} \right)x + m + 2\]

Hàm số đồng biến trên \[\mathbb{R}\] \[ \Leftrightarrow y’ \geqslant 0,\forall x \in \mathbb{R}\]

\[ \Leftrightarrow \left\{ \begin{gathered}
\Delta’ \leqslant 0 \hfill \\
3m > 0 \hfill \\
\end{gathered} \right. \Leftrightarrow \left\{ \begin{gathered}
4{m^2} + 4m + 1 – 3m\left( {m + 2} \right) \leqslant 0 \hfill \\
m > 0 \hfill \\
\end{gathered} \right.\]

\[ \Leftrightarrow \left\{ \begin{gathered}
{\left( {m – 1} \right)^2} \leqslant 0 \hfill \\
m > 0 \hfill \\
\end{gathered} \right. \Leftrightarrow m = 1{\text{ }}\left( {TM} \right)\]

Vậy \[m = 1\].

Câu 2. Tìm các giá trị của tham số m để hàm số \[y = \frac{{x – m}}{{2x – 1}}\] đồng biến trên từng khoảng xác định.

Hướng dẫn giải

TXĐ: \[D = \mathbb{R}\backslash \left\{ {\frac{1}{2}} \right\}\]. Ta có: \[y’ = \frac{{ – 1 + 2m}}{{{{\left( {2x – 1} \right)}^2}}}\]

Hàm số đồng biến trên từng khoảng xác định \[ \Leftrightarrow y’ \geqslant 0,\forall x \in D\] \[ \Leftrightarrow – 1 + 2m > 0 \Leftrightarrow m > \frac{1}{2}\]

Vậy \[m > \frac{1}{2}\]

Câu 3. Tìm m để hàm số \[y = – {x^3} + 3{x^2} + \left( {m–1} \right)x + m\] nghịch biến trên khoảng \[\left( { – 1; + \infty } \right)\]

Hướng dẫn giải

TXĐ: \[D = \mathbb{R}\]. Ta có: \[y’ = – 3{x^2} + 6x + m–1\]

Hàm số nghịch biến trên khoảng \[\left( { – 1; + \infty } \right)\] \[ \Leftrightarrow y’ \leqslant 0,\forall x \in \left( { – 1; + \infty } \right)\]

\[ \Leftrightarrow m \leqslant 3{x^2} – 6x + 1,\forall x \in \left( { – 1; + \infty } \right){\text{ }}\left( 1 \right)\]

Xét hàm số \[g\left( x \right) = 3{x^2}–6x + 1\] trên khoảng \[\left( { – 1; + \infty } \right)\]

\[g’\left( x \right) = 6x–6\]

\[g’\left( x \right) = 0 \Leftrightarrow x = 1\]

Bảng biến thiên

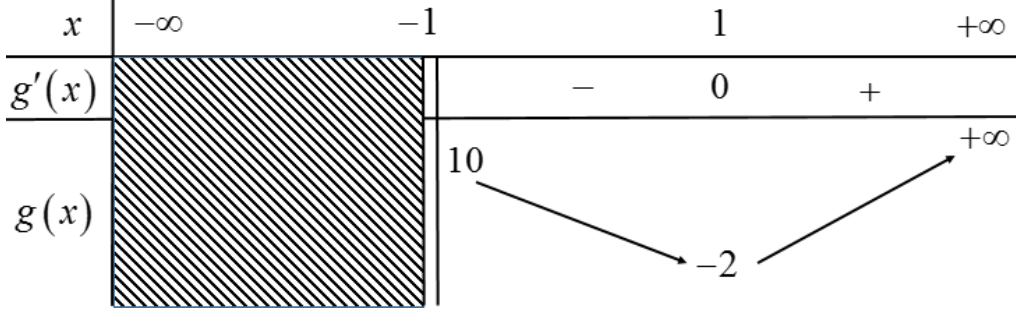
Dựa vào bảng biến thiên ta có: \[\mathop {\min }\limits_{\left( { – 1; + \infty } \right)} g\left( x \right) =  – 2\]

Do đó \[\left( 1 \right) \Leftrightarrow m \leqslant \mathop {\min }\limits_{\left( { – 1; + \infty } \right)} g\left( x \right) \Leftrightarrow m \leqslant  – 2\]

Vậy \[m \leqslant – 2\] thoả yêu cầu bài toán

Câu 4. Có bao nhiêu giá trị nguyên của tham số m để hàm số \[y = \frac{{x + 6}}{{x + 5m}}\] nghịch biến trên khoảng \[\left( {10; + \infty } \right)\]?

Hướng dẫn giải

TXĐ: \[D = \mathbb{R}\backslash \left\{ {5m} \right\}\]

Ta có: \[y’ = \frac{{5m – 6}}{{{{\left( {x + 5m} \right)}^2}}}\]. Để hàm số nghịch biến trên khoảng \[\left( {10; + \infty } \right)\] thì

\[\left\{ \begin{gathered}
y’ < 0 \hfill \\
– 5m \notin \left( {10; + \infty } \right) \hfill \\
\end{gathered} \right. \Leftrightarrow \left\{ \begin{gathered}
5m – 6 < 0 \hfill \\
– 5m \leqslant 10 \hfill \\
\end{gathered} \right. \Leftrightarrow \left\{ \begin{gathered}
m < \frac{6}{5}\begin{array}{*{20}{c}}
{} \\
{}
\end{array} \hfill \\
m \geqslant – 2 \hfill \\
\end{gathered} \right.\]

Do \[m \in \mathbb{Z} \Rightarrow m \in \left\{ { – 2; – 1;0;1} \right\}\]

Câu 5. Tìm m để hàm số \[y = – {x^3} + 3{x^2} + \left( {m–1} \right)x + 2m–3\] đồng biến trên đoạn có độ dài lớn nhất bằng 3?

Hướng dẫn giải

TXĐ: \[D = \mathbb{R}\]. Ta có: \[y’ = – 3{x^2} + 6x + m–1\]

Vì hệ số của \[{x^2}\] của \[{y’}\] là \[ – 3 < 0\] nên hàm số đã cho đồng biến trên đoạn có độ dài lớn nhất bằng 3 khi và chỉ khi \[y’ = 0\] có 2 nghiệm \[{x_1},{x_2}\] phân biệt thoả mãn \[\left| {{x_2} – {x_1}} \right| = 3\]

\[ \Leftrightarrow \left\{ \begin{gathered}
\Delta’ = 9 + 3\left( {m – 1} \right) > 0 \hfill \\
{\left( {{x_1} + {x_2}} \right)^2} – 4{x_1}{x_2} = 9 \hfill \\
\end{gathered} \right.{\text{ }}\left( * \right)\]

Theo Vi-et ta có: \[\left\{ \begin{gathered}
{x_1} + {x_2} = 2 \hfill \\
{x_1}{x_2} = \frac{{1 – m}}{3}\begin{array}{*{20}{c}}
{} \\
{}
\end{array} \hfill \\
\end{gathered} \right.\]

Do đó:

\[\left( * \right) \Leftrightarrow \left\{ \begin{gathered}
m > – 2 \hfill \\
4 + 4 \cdot \frac{{m – 1}}{3} = 9\begin{array}{*{20}{c}}
{} \\
{}
\end{array} \hfill \\
\end{gathered} \right.\] \[ \Leftrightarrow \left\{ \begin{gathered}
m > – 2 \hfill \\
m = \frac{{19}}{4}\begin{array}{*{20}{c}}
{} \\
{}
\end{array} \hfill \\
\end{gathered} \right.\] \[ \Leftrightarrow m = \frac{{19}}{4}\]

Vậy \[m = \frac{{19}}{4}\]