Đến với toán hình, các bạn học sinh có cơ hội tiếp cận đến rất nhiều dạng hình học khác nhau, hiểu được khái niệm của chúng và cách tìm chu vi hoặc diện tích của mỗi loại. Trong bài viết này, chúng tôi sẽ mang đến cho bạn các kiến thức xoay quanh đa giác và cách tính diện tích đa giác dễ hiểu nhất.
1. Bật mí khái niệm về đa giác và cách phân loại
1.1 Định nghĩa đa giác là gì
- Đa giác là một dạng hình học không gian khép kín được tạo nên bằng cách ghép nối nhiều đoạn thẳng liên tiếp nhau trên một mặt phẳng.
- Toàn bộ phần bị giới hạn bởi các đoạn thẳng khác nhau tạo nên hình đa giác sẽ được gọi là phân trong của chính đa giác đó.
- Các đoạn thẳng tạo nên đa giác được gọi là cạnh của đa giác.
- Điểm kết nối giữa hai cạnh trong hình lại với nhau được gọi là đỉnh của hình đa giác.
- Ngoài ra, đoạn thẳng mà nối hai đỉnh không nằm kề nhau trong hình đa giác được định nghĩa là đường chéo của hình.
1.2 Phân loại
Một hình đa giác được cấu thành nên bởi nhiều đoạn thẳng hay còn gọi là cạnh của đa giác, kết hợp với các góc vô cùng lớn. Sau đây sẽ là cách phân loại đa giác chi tiết và dễ hiểu nhất cho học sinh:
- Đa giác lồi: Khi quan sát, bạn có thể thấy toàn bộ hình đa giác này đang nằm về một phía của đường thẳng chứa cạnh bất kỳ của đa giác đo .
- Đa giác lõm: Đa giác sẽ nằm tại vị trí nghiêng về 2 hai phía của ít nhất một đường thẳng đang chứa cạnh của đa giác đó.
- Đa giác đơn: Các cạnh trong hình chỉ cắt nhau tại phần đỉnh của đa giác và không có hai cạnh bất kỳ nào kề nhau.
- Đa giác không đơn: Đây là dạng đa giác mà có hai cạnh không kề cũng không cắt nhau hoặc điểm cắt nhau giữa chúng không phải là đỉnh của đa giác đó.
- Đa giác đều: Đây là dạng đa giác phổ biến nhất mà chúng ta được tiếp xúc và toàn bộ các cạnh và góc của chúng đều bằng nhau. Ví dụ như tam giác đều, hình vuông,…
2. Bật mí cách tính diện tích đa giác bất kỳ và bài tập có đáp án kèm theo
2.1 Công thức tìm diện tích đa giác đều
\[S=\frac{a\times p}{2}\]
Trong đó:
- p được xem là chu vi của đa giác (và chu vi sẽ bằng tổng độ dài của toàn bộ các cạnh trong đa giác đó).
- a là chiều dài của trung đoạn, mà trung đoạn là đoạn thẳng vuông góc với cạnh và đi qua tâm của chính đa giác đó.
Ví dụ minh hoạ: Cho một lục giác đều có 6 cạnh và mỗi cạnh dài 10cm. Hãy tính diện tích đa giác đều này là bao nhiêu ?
Giải:
- Bước 1: Ta cần tính chu vi của hình lục giác bằng: \[p=6\times 10=60cm\]
- Bước 2: Cần tìm trung đoạn, biết rằng lục giác đều có 6 cạnh (n) và mỗi cạnh có độ dài là 10cm. Áp dụng cả hai giá trị trên vào biểu thức ta được \[2\tan(180\div 6)=1,1547\]. Tiếp đến, ta chia 10 cho 1,1547 để tìm ra được giá trị của trung đoạn là 8,66.
- Bước 3: Suy ra diện tích của đa giác đều này là: \[\frac{a\times p}{2}=\frac{8,66\times 60}{2}=259,8 cm^2\]
3.2 Công thức tìm diện tích đa giác không đều
- Bước 1: Bạn có thể tiến hành chia đa giác lớn thành các hình nhỏ như tam giác, hình vuông, hình thoi, hình bình hành,…
- Bước 2: Tiến hành tính diện tích của từng hình đa giác nhỏ đã chia
- Bước 3: Tính tổng toàn bộ diện tích các đa giác nhỏ và đây chính là diện tích đa giác lớn cần tìm.
Trong đó:
- Diện tích tam giác là: \[s=\frac{1}{2}\times a\times h\], với a là độ dài cạnh đối diện và h là chiều cao của hình.
- Diện tích hình vuông: \[S=a^2\] với a là độ dài cạnh của hình
- Diện tích hình bình hành: \[s=h\times a\] với h là chiều cao và a là cạnh tương ứng với chiều cao đó.
- Diện tích hình chữ nhật: \[s=a\times b\], trong đó a và b lần lượt là chiều dài và chiều rộng của hình.
Ví dụ: Hãy tính diện tích của hình đa giác ABCDE, biết rằng BG = 19CM, AC = 48CM, AH=8CM, HK=18CM, KC= 22CM, EH=16CM, KD=23CM.
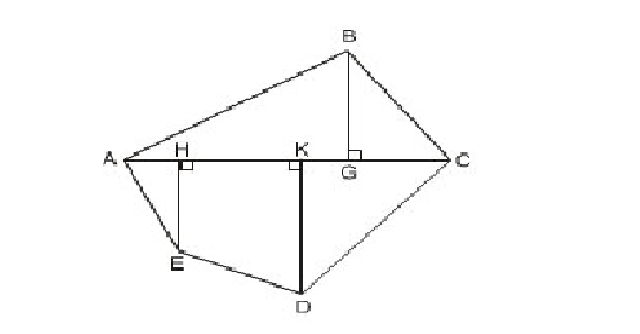
Giải:
Ta chia đa giác ABCDE thành tam giác ABC, hai tam giác vuông là AHE và DKC, hình thang vuông HKDE như hình trên.
\[S_{ABC}=\frac{1}{2}\times BG\times AC=\frac{1}{2}\times 19\times 48=456 cm^2 \]
\[S_{AHE}=\frac{1}{2}\times AH\times HE=\frac{1}{2}\times 8\times 16=64 cm^2 \]
\[S_{DKC}=\frac{1}{2}\times KC\times KD=\frac{1}{2}\times 22\times 23=253 cm^2 \]
\[S_{HKDE}=\frac{1}{2}HK\times(HE+KD)=\frac{1}{2}\times 18\times(16+23)=351 cm^2 \]
\[\Rightarrow S_{ABCDE}=S_{ABC}+S_{AHE}+S_{DEK}+S_{HKDE}\]
\[=456+64+253+351=1124 cm^2\]
\[\Rightarrow S_{ABCDE}=1124 cm^2\]
Bài viết trên đã mang đến cho toàn thể các bạn học sinh phương pháp tính diện tích đa giác đều và không đều. Mong rằng, những thông tin mà chúng tôi chia sẻ đã giúp bạn vững vàng và tự tin hơn để đối diện mọi kỳ kiểm tra sắp đến.