Xuyên suốt quá trình tìm hiểu về toán hình, các bạn học sinh sẽ được dịp tiếp cận đến rất nhiều dạng góc khác nhau. Trong đó, góc ở vị trí đặc biệt – tia phân giác của một góc là những kiến thức cốt lõi bạn cần phải nắm để giải được những dạng bài tập phức tạp. Hiểu được tính quan trọng đó, chúng tôi đã thực hiện bài viết này để tổng hợp kiến thức cho bạn.
1. Bật mí các góc ở vị trí đặc biệt cần nhớ
1.1 Hai góc kề bù
- Nếu hai góc mà có một cạnh chung và hai cạnh còn lại là hai tia đối nhau thì ta nói chúng là hai góc kề bù. Theo đó, hai góc kề bù nếu cộng lại sẽ có tổng số đo là \[ 180\degree\].
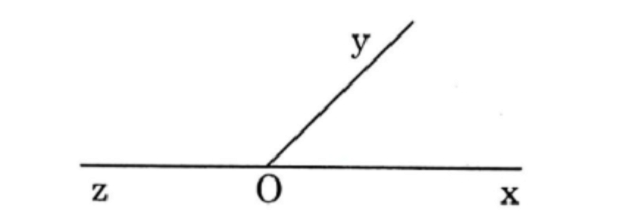
- Bên cạnh đó, hai góc kề bù còn được hiểu là hai góc vừa kề và vừa bù nhau.
- Hai góc kề nhau sẽ là hai góc có một cạnh chung nằm giữa, còn hai cạnh còn lại sẽ nằm khác phía nhau nếu so với cạnh chung đó.
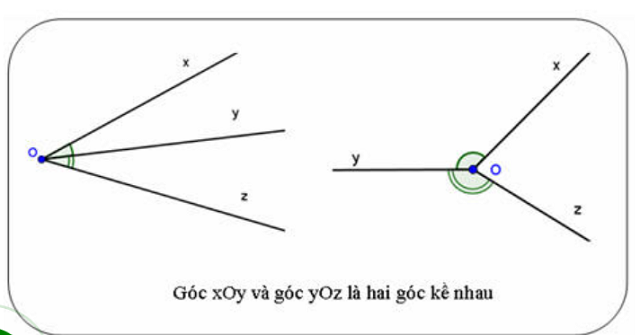
- Hai góc bù nhau là khái niệm chỉ hai góc có tổng số đo là \[ 180\degree\].
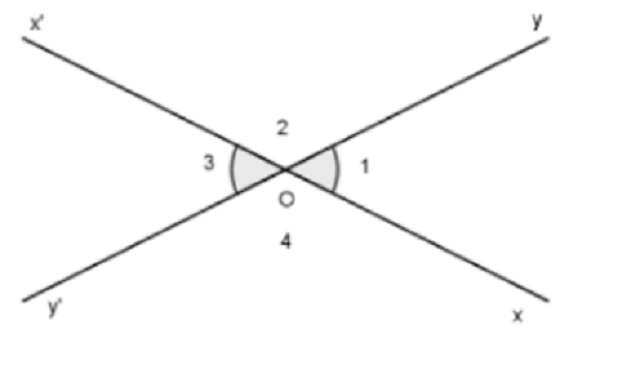
1.2 Hai góc đối đỉnh
Theo khái niệm, hai góc đối đỉnh được hiểu là hai góc mà mỗi cạnh của góc này lại là tia đối của một cạnh thuộc góc kia. Tính chất của hai góc đối đỉnh là chúng luôn luôn bằng nhau dù nằm khác hướng.
2. Mách bạn khái niệm tia phân giác của một góc là gì
2.1 Định nghĩa
Nếu ta có một tia nằm giữa hai cạnh của một góc, và tạo với hai cạnh ấy thành hai góc bằng nhau, thì tia này được gọi là tia phân giác của chính góc đó. Ngoài ra, đường thẳng mà chứa tia phân giác kể trên sẽ được định nghĩa là đường phân giác của góc đó. Tính chất của tia phân giác sẽ được thể hiện rõ qua mô tả theo công thức toán như sau:
\[\widehat{xOz}=\widehat{yOz}=\frac{1}{2}\widehat{xOy}\]
Trong đó: Oz là tia phân giác của góc xOy đang xét.
- Định lý thuận: Tất cả các điểm cùng nằm trên tia phân giác của góc đó, thì khoảng cách từ điểm đó tới hai cạnh của góc sẽ luôn bằng nhau.
- Định lý đảo: Các điểm nằm bên trong góc và cách đều hai cạnh của góc thì nằm trên đường phân giác của góc đó. Ngoài ra, tia mà tập hợp tất cả các điểm cùng nằm bên trong góc và cách đều hai cạnh của góc là tia phân giác của chính góc đó.
2.3 Một số tính chất của tia phân giác
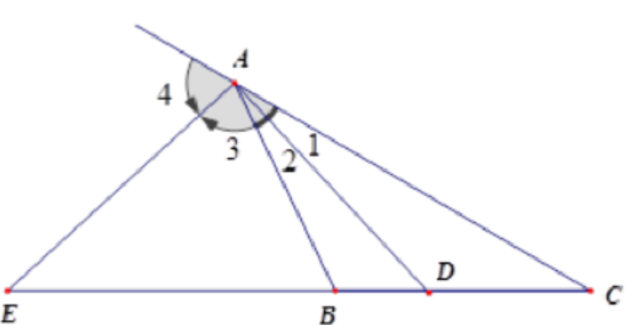
Nếu xét trong tam giác, đường phân giác của góc sẽ chia cạnh đối diện của góc đó thành hai đoạn thẳng có chung tỷ lệ với hai cạnh kề hai đoạn ý. Hơn cả thế, định lý này còn luôn đúng với tia phân giác của góc nằm ngoài tam giác.
Ví dụ minh hoạ: Biết tam giác ABC có 2 đoạn thẳng là AD và E là đường phân giác của góc trong và góc ngoài thuộc đỉnh A tam giác, khi đó ta sẽ có:
\[\frac{DC}{BC}=\frac{AB}{AC};\frac{EB}{EC}=\frac{AB}{AC}\]
3. Những dạng bài tập về góc ở vị trí đặc biệt – tia phân giác của một góc
3.1 Chứng minh tia phân giác
- Cách 1: Đối với dạng bài tập này mục tiêu cần đạt được là chứng minh đường thẳng Oy sẽ là tia phân giác của góc xOz. Phương pháp làm là chứng minh 2 điểm bất kỳ thuộc Oy có khoảng cách lần lượt đến Ox và Oz bằng nhau .
- Cách 2: Cần chứng minh định lý tia phân giác trong góc: \[\widehat{xOz}=\widehat{yOz}=\frac{1}{2}\widehat{xOy}\]
- Cách 3: Dùng tính chất của đường trung tuyến trong tam giác cân đồng thời là tia phân giác của tam giác đó.
Bài tập: Ta có tam giác ABC với hai đường phân giác góc ngoài của đỉnh B và C cắt nhau tại E. Hãy chứng minh điểm E nằm trên đường phân giác của góc BAC.
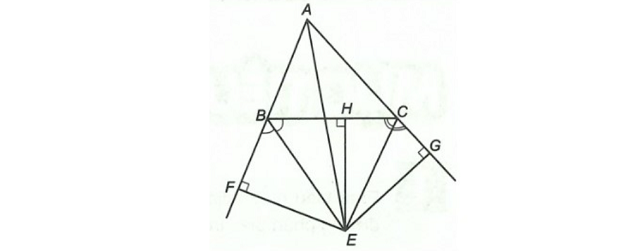
Giải: Vẽ từ định E lần lượt EH vuông góc với BC, và EF vuông góc và AB, EG vuông góc với AC (trong đó các điểm H thuộc BC, F thuộc AB và G thuộc AC).
Suy ra:
EF= EH ( Vì điểm E nằm trên đường phân giác ngoài của góc FBC) (1)
EH=EG ( Vì điểm E nằm trên phân giác ngoài của góc HCG) (2)
Từ (1) và (2) ta có thể suy ra được: EF=EG
Kết luận: E thuộc tia phân giác trong của góc BAC (theo tính chất tia phân giác của một góc).
Dạng 2: Tìm số đo góc
Bài tập: Ta có hai góc AOB và BOC là hai góc kề nhau, mà \[\widehat{AOB}=50\degree,\widehat{BOC}=80\degree\]. Biết OD là tia đối của OC. Hãy tính:
- a) Số đo góc của AOC
- b) Chứng minh rằng tia OA nằm giữa tia OB và OD.
- c) Chứng minh OA là phân giác của góc BOD.\

Giải:
- a) Ta có: \[\widehat{AOC}=\widehat{AOB}+\widehat{BOC}=50+80=130\degree\]
- b) Ta có:
\[\widehat{AOC}<\widehat{COD}(130\degree<180\degree),\widehat{COB}<\widehat{AOC}(80\degree<130\degree)\]
Vì thế, tia OA sẽ nằm giữa hai tia OB và OD
- c) Vì tia OA nằm giữa tia OB và OD
\[\Rightarrow\widehat{COD}=\widehat{COA}+\widehat{AOD}\Rightarrow\widehat{AOD}=50\degree\]
Suy ra: \[\Rightarrow\widehat{AOD}=\widehat{AOB}=50\degree\]
Vậy, OA là tia phân giác của góc BOD.
Bài viết trên đã mang đến chuyên đề góc ở vị trí đặc biệt – tia phân giác của một góc chi tiết và cụ thể nhất. Mong rằng, những thông tin mà chúng tôi đã cung cấp sẽ giúp bạn có thêm nhiều kiến thức toán học thú vị và cảm thấy vui vẻ hơn trong quá trình học tập của chính mình.