Giải hệ phương trình bằng phương pháp thế và phương pháp cộng đại số

Giải hệ phương trình là một chủ đề quan trọng trong đại số và được ứng dụng trong nhiều lĩnh vực khác nhau. Hiện nay, có nhiều phương pháp giải hệ phương trình khác nhau, trong đó phương pháp thế và phương pháp cộng đại số là hai phương pháp phổ biến và được sử dụng rộng rãi. Trên cơ sở đó, trong bài viết này, chúng ta sẽ tìm hiểu cách giải hệ phương trình bằng hai phương pháp này và áp dụng chúng để giải một số bài tập thực tế.

Giải hệ phương trình bằng phương pháp thế

Quy tắc thế

Quy tắc thế cũng có thể được sử dụng để biến đổi một hệ phương trình đại số thành hệ phương trình tương đương, giúp giải quyết vấn đề phức tạp hơn một cách dễ dàng và nhanh chóng.

Cụ thể, để biến đổi một hệ phương trình đại số thành hệ phương trình tương đương bằng quy tắc thế, ta có thể thực hiện các bước sau:

1. Tìm một biến trong một phương trình và giải nó ra dưới dạng biểu thức của các biến khác.
2. Thay thế biểu thức đó vào các phương trình khác trong hệ.
3. Thực hiện các phép tính đơn giản để đưa hệ phương trình về dạng tương đương.

Ví dụ, giả sử ta có hệ phương trình đại số sau:

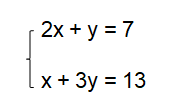
Để giải hệ phương trình này bằng quy tắc thế, ta có thể thực hiện các bước sau:

• Từ phương trình thứ nhất, ta có:

y = 7 - 2x

• Thay thế biểu thức này vào phương trình thứ hai, ta có:

x + 3(7 - 2x) = 13

• Giải phương trình trên để tìm x:

x + 21 - 6x = 13
-5x = -8
x = 8/5

• Thay x vào biểu thức của y, ta có:

y = 7 - 2 × (8/5) = 1/5

Vậy nghiệm của hệ phương trình là x = 8/5, y = 1/5. Ta đã giải được hệ phương trình bằng phương pháp quy tắc thế.

Áp dụng quy tắc thế

Phương pháp thế là một phương pháp giải hệ phương trình đại số. Cách giải bằng phương pháp thế được thực hiện như sau:

1. Tìm một biến ở một phương trình và giải nó ra dưới dạng biểu thức của các biến khác.
2. Thay biểu thức vừa tìm được vào các phương trình khác trong hệ để loại bỏ biến đó.
3. Lặp lại các bước trên cho đến khi chỉ còn một phương trình với một ẩn.
4. Giải phương trình với một ẩn để tìm giá trị của ẩn đó.
5. Thay giá trị của ẩn vào các phương trình khác để tìm giá trị của các ẩn còn lại.

Đây là một phương pháp đơn giản và dễ hiểu. Tuy nhiên, phương pháp thế không phải là phương pháp tối ưu cho mọi trường hợp, đặc biệt là đối với những hệ phương trình lớn và phức tạp. Trong trường hợp đó, ta cần áp dụng các phương pháp khác như phương pháp đơn giản hóa Gauss, phương pháp Gauss-Jordan hay phương pháp lập ma trận để giải hệ phương trình một cách chính xác và hiệu quả hơn.

Luyện tập

Bài tập 1: Giải hệ phương trình sau bằng phương pháp thế:

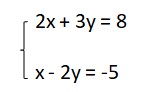
Cách giải:

Bước 1: Tìm biến trong một phương trình và giải nó ra

Ta sẽ giải biến x trong phương trình thứ nhất:

2x + 3y = 8
2x = 8 - 3y
x = (8 - 3y) / 2

Bước 2: Thay biến vừa giải được vào phương trình còn lại và giải phương trình đó

Thay x = (8 - 3y) / 2 vào phương trình thứ hai:

x - 2y = -5
((8 - 3y) / 2) - 2y = -5
8 - 3y - 4y = -10
-7y = -18
y = 18 / 7

Bước 3: Tìm giá trị của biến còn lại bằng cách thay giá trị của biến đã tìm vào phương trình đã giải ở bước 1

x = (8 - 3y) / 2
x = (8 - 3(18/7)) / 2
x = -1/7

Vậy nghiệm của hệ phương trình là (x, y) = (-1/7, 18/7).

Bài tập 2: Giải hệ phương trình sau bằng phương pháp thế:

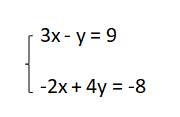
Cách giải:

Bước 1: Tìm biến trong một phương trình và giải nó ra

Ta sẽ giải biến x trong phương trình thứ nhất:

3x - y = 9
3x = y + 9
x = (y + 9) / 3

Bước 2: Thay biến vừa giải được vào phương trình còn lại và giải phương trình đó

Thay x = (y + 9) / 3 vào phương trình thứ hai:

-2x + 4y = -8
-2((y + 9) / 3) + 4y = -8
(-2/3)y - 6 + 4y = -8
(10/3)y = -2
y = -6/5

Bước 3: Tìm giá trị của biến còn lại bằng cách thay giá trị của biến đã tìm vào phương trình đã giải ở bước 1

x = (y + 9) / 3
x = ((-6/5) + 9) / 3
x = 1/5

Vậy nghiệm của hệ phương trình là `(x, y) = (1/5).

Giải hệ phương trình bằng phương pháp cộng đại số

Quy tắc cộng đại số

Phương pháp cộng đại số được sử dụng để giải hệ phương trình bằng cách tìm các giá trị của các biến mà thỏa mãn đồng thời tất cả các phương trình trong hệ.

Cách giải hệ phương trình bằng phương pháp cộng đại số gồm các bước sau:

Bước 1: Sắp xếp hệ phương trình theo dạng chuẩn, tức là sắp xếp các biến theo thứ tự tăng dần.

Bước 2: Dùng quy tắc cộng đại số để loại bỏ các biến không mong muốn khỏi từng phương trình trong hệ. Điều này thường được thực hiện bằng cách cộng thích hợp các phương trình trong hệ với nhau.

Bước 3: Tìm giá trị của một biến bằng cách sử dụng phương trình sau khi loại bỏ các biến không mong muốn.

Bước 4: Sử dụng giá trị của biến tìm được trong bước 3 để tìm giá trị của các biến khác bằng cách thay vào các phương trình còn lại trong hệ.

Dưới đây là ví dụ minh họa về cách giải hệ phương trình bằng phương pháp cộng đại số:

Giải hệ phương trình sau bằng phương pháp cộng đại số:

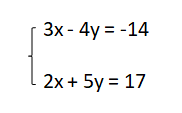
Bước 1: Sắp xếp hệ phương trình theo dạng chuẩn:

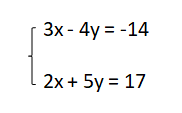
Bước 2: Sử dụng quy tắc cộng đại số để loại bỏ x trong phương trình thứ 2:

3x - 4y = -14

6x + 15y = 51

<=> 3x + 11y = 37

Bước 3: Sử dụng phương trình vừa tìm được để tìm giá trị của y:

3x + 11y = 37

=> 11y = 37 - 3x

=> y = (37 - 3x)/11

Bước 4: Sử dụng giá trị của y trong phương trình ban đầu để tìm giá trị của x:

3x - 4y = -14

3x - 4[(37 - 3x)/11] = -14

=> 33x - 4(37 - 3x) = -154

=> 33x - 148 = -154

=> 33x = -6

=> x = -6/33

Vậy nghiệm của hệ phương trình là (x, y) = (-6/33, 5/33).