Hệ hai phương trình bậc nhất hai ẩn

Hệ phương trình tương đương là một khái niệm quan trọng trong đại số và giải tích, được áp dụng trong nhiều lĩnh vực khác nhau như toán học, vật lý, kinh tế học và các ngành khoa học khác. Nó được sử dụng để miêu tả một nhóm các phương trình có cùng các nghiệm. Việc giải hệ phương trình tương đương là giải các phương trình này cùng một lúc để tìm ra giá trị của các biến số mà thỏa mãn tất cả các phương trình trong hệ.

Trong bài viết này, chúng ta sẽ tìm hiểu về khái niệm hệ phương trình tương đương, cách giải và áp dụng trong thực tế. Chúng ta cũng sẽ đi sâu vào một số ví dụ về hệ phương trình tương đương để giúp bạn hiểu rõ hơn về khái niệm này.

Khái niệm về hệ hai phương trình bậc nhất hai ẩn

Hệ hai phương trình bậc nhất hai ẩn là một hệ gồm hai phương trình bậc nhất cùng hai ẩn x và y có dạng như sau:

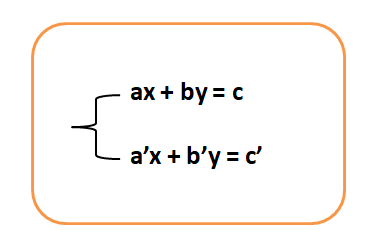
Trong đó a, b, c, a', b', c' là các hằng số đã biết. Mục tiêu của việc giải hệ phương trình này là tìm ra các giá trị của x và y sao cho cả hai phương trình đều được thỏa mãn.

Hệ hai phương trình bậc nhất hai ẩn có thể có các trường hợp sau:

• Hệ có một nghiệm duy nhất (x, y)
• Hệ vô nghiệm, tức là không có cặp số nào thỏa mãn cả hai phương trình đồng thời
• Hệ có vô số nghiệm, tức là có vô số cặp số (x, y) thỏa mãn cả hai phương trình đồng thời

Có nhiều phương pháp để giải hệ hai phương trình bậc nhất hai ẩn, trong đó phương pháp cộng trừ phương trình là phương pháp đơn giản và thường được sử dụng.

Minh hoạ hình học tập nghiệm của hệ phương trình bậc nhất hai ẩn

Giả sử chúng ta có hệ phương trình bậc nhất hai ẩn:

 

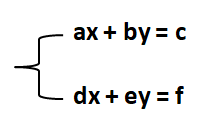
Trong đó a, b, c, d, e, f là các hằng số và x, y là các biến số cần tìm. Để giải hệ phương trình này, ta có thể sử dụng phương pháp cộng trừ để loại bỏ một biến số và tính giá trị của biến số còn lại.

Tuy nhiên, nếu xem xét một cách hình học, hệ phương trình này có thể được biểu diễn dưới dạng hai đường thẳng trên mặt phẳng tọa độ. Vì mỗi phương trình bậc nhất hai ẩn đều biểu diễn một đường thẳng trên mặt phẳng tọa độ, nên hệ phương trình này sẽ tương ứng với hai đường thẳng trên mặt phẳng tọa độ.

Hai đường thẳng này có thể cắt nhau, song song hoặc trùng nhau trên mặt phẳng tọa độ. Tùy vào vị trí tương đối của hai đường thẳng này mà ta có thể suy ra tập nghiệm của hệ phương trình này.

Nếu hai đường thẳng cắt nhau tại một điểm duy nhất, thì tập nghiệm của hệ phương trình sẽ là cặp giá trị (x, y) của điểm đó.

Nếu hai đường thẳng song song và không trùng nhau, nghĩa là chúng không cắt nhau trên mặt phẳng tọa độ, thì hệ phương trình này sẽ không có nghiệm.

Nếu hai đường thẳng trùng nhau, nghĩa là chúng có dạng giống nhau, thì hệ phương trình sẽ có vô số nghiệm.

Vậy, qua một cách tiếp cận hình học, ta có thể dễ dàng suy ra tập nghiệm của hệ phương trình bậc nhất hai ẩn.

Để minh hoạ hình học tập nghiệm của hệ phương trình bậc nhất hai ẩn tổng quát, ta có thể sử dụng đồ thị hệ số góc và điểm cắt của hai đường thẳng tương ứng với hai phương trình.

Giả sử ta có hệ phương trình:

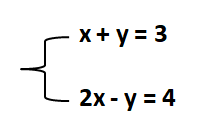
Để giải hệ phương trình này, ta có thể áp dụng phương pháp Cramer hoặc phương pháp khác. Tuy nhiên, để minh hoạ hình học, ta có thể vẽ đồ thị cho hai phương trình này:

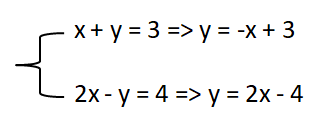
Để vẽ đồ thị, ta có thể chuyển hai phương trình về dạng y = ax + b:

Sau đó, ta có thể vẽ hai đường thẳng tương ứng trên hệ trục tọa độ Oxy:

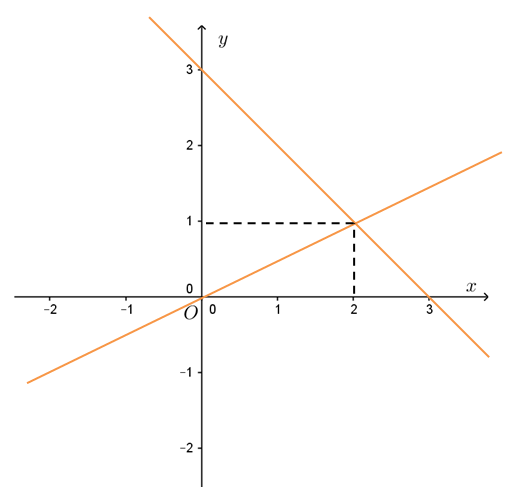
Ta thấy rằng hai đường thẳng này cắt nhau tại một điểm duy nhất có tọa độ (2, 1). Do đó, tập nghiệm của hệ phương trình bậc nhất hai ẩn này là {x = 2, y = 1}.

Hệ phương trình tương đương

Hệ phương trình tương đương là một tập hợp các phương trình mà các phương trình trong tập hợp này có cùng tập nghiệm. Các phương trình trong hệ phương trình tương đương có thể được chuyển đổi từ các phương trình khác nhau bằng cách sử dụng các phép biến đổi đẳng thức hợp lệ, mà không ảnh hưởng đến tập nghiệm của hệ phương trình. Hệ phương trình tương đương thường được sử dụng trong việc giải các bài toán đại số, trong đó cần phải tìm tập nghiệm chung của một tập hợp các phương trình.

Ví dụ về hệ phương trình tương đương:

Cho hệ phương trình sau:

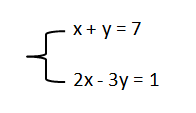
Chúng ta có thể biến đổi hệ phương trình trên thành hệ phương trình tương đương bằng cách loại bỏ biến số x hoặc y trong một trong hai phương trình và giải quyết hệ phương trình mới này.

Ví dụ, để loại bỏ biến số $x$ trong phương trình thứ hai, ta có thể nhân cả hai vế của phương trình đó với số -1 và cộng với phương trình đầu tiên, ta được:

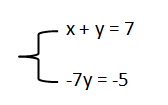
Sau đó giải phương trình tương đương này, ta thu được giá trị \(y = \frac{5}{7}\). Tiếp theo, ta có thể dùng giá trị này để tìm giá trị $x$ bằng cách thay vào phương trình đầu tiên:

\(x + \frac{5}{7} = 7 \Rightarrow x = \frac{44}{7}\)

Vậy tập nghiệm của hệ phương trình ban đầu là (x, y ) = (\(\mathrm{\frac{5}{7}}\); \(\mathrm{\frac{44}{7}}\))