Quan hệ chia hết và tính chất
Trong toán học, quan hệ chia hết là một khái niệm cơ bản và quan trọng trong lĩnh vực số học. Nó giúp ta hiểu được quan hệ giữa các số và cách chúng tương tác với nhau. Cụ thể, nếu một số được chia hết cho một số khác mà không có số dư, ta nói số đó chia hết cho số kia. Việc hiểu và áp dụng quan hệ chia hết vào các bài toán toán học là rất quan trọng trong việc giải quyết các vấn đề thực tế trong cuộc sống. Bài viết này sẽ giải thích chi tiết về quan hệ chia hết và các tính chất liên quan đến nó, giúp bạn hiểu rõ hơn về khái niệm này và áp dụng nó vào các bài toán thực tế.
Quan hệ chia hết
Khi nào thì a chia hết cho b?
Cho số tự nhiên a, b và x, trong đó b # 0, a chia hết cho b khi b.x = a, ta nói a chia hết cho b và ta có phép chia hết a ⋮ b = x
Nếu a không chia hết cho b, ta kí hiệu là a ⋮̸ b
Ước và bội
Nếu có số tự nhiên a chia hết cho số tự nhiên b thì ta nói a là bội của b, còn b là ước của a
Kí hiệu: Ư(a) là tập hợp các ước của a và B(b) là tập hợp các bội của b.
Ví dụ:
a) 12 ⋮ 6
⇒ 12 là bội của 6.
Còn 6 được gọi là ước của 12
b) Nếu chúng ta xem xét số nguyên 5, thì bội số của nó là 5, 10, 15, 20, 25, v.v.
Một ví dụ điển hình để minh họa khái niệm bội và ước là xét số 12. Các bội của 12 là 12, 24, 36, 48, 60, v.v. Các ước của 12 là 1, 2, 3, 4, 6 và 12. Trong trường hợp này, chúng ta có thể thấy rằng 12 có 6 ước là bội của chính nó.
3 là ước của 21, vì 21 chia hết cho 3 (bằng 7).
Cách tìm ước và bội
Tìm ước:
Ta có thể tìm các ước của a (a > 1) bằng cách lần lượt a (a > 1) bằng cách lần lượt chia a cho các số tự nhiên từ 1 đến a để xét xem a chia hết cho những số nào, khi đó các số ấy là ước của a.
Ví dụ:
24 : 1 = 24
24 : 2 = 12
24 : 4 = 8
24 : 8 = 4
24 : 24 = 1
Vậy các ước của 24 là 1; 2; 4; 8; 24. Tập hợp các ước của 24 là: Ư(24) = {1; 2; 4; 8; 24}
Tìm bội:
Ta có thể tìm các bội của một số khác 0 bằng cách nhân số đó lần lượt với 1, 2, 3,...
Ví dụ:
Ta lấy 7 nhân với từng số thì được bội của 7, lấy 7.1 = 7 nên 7 là bội của 7, 7.2 = 14 nên 14 là bội của 7,...
Vậy B(7) = {7; 14; 21;...}
Tính chất chia hết của một tổng
Tính chất 1
Nếu tất cả các số hạng của một tổng đều chia hết cho cùng một số thì tổng chia hết cho số đó.
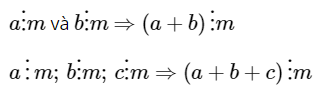
Tính chất 2
Nếu chỉ có một số hạng của tổng không chia hết cho một số, còn các số hạng khác đều chia hết cho số đó thì tổng không chia hết cho số đó.
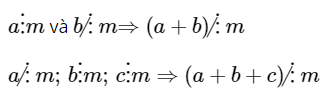
Ví dụ:
4 ⋮ 2, 8 ⋮ 2, 22 ⋮ 2 => (4 + 8 + 22) ⋮ 2 = 34 ⋮ 2
Bài tập
Bài 1: Tìm tập hợp các ước và bội
a) Hãy tìm tất cả các ước của 20
b) Hãy tìm tất cả các bội nhỏ hơn 50 của 4
Đáp án:
a) Tất cả các ước của 20 là: 1; 2; 4; 5; 10; 20
b) Tất cả các bội nhỏ hơn 50 của 4 là: 0; 4; 8; 12; 16; 20 ;24; 28; 32; 36; 40; 44; 48
Bài 2:
Không thực hiện phép tính, hãy cho biết:
a) 40 + 27 có chia hết cho 5 không? Vì sao?
b) 12 + 30 – 18 có chia hết cho 6 không? Vì sao?
Đáp án:
a) 20 + 81 không chia hết cho 5 vì 40 chia hết cho 5 nhưng 27 không chia hết cho 5
b) 12 + 30 – 18 chia hết cho 6 vì 12, 30 và 18 đều chia hết cho 6.
