Tášp háŧĢp sáŧ háŧŊu táŧ
Trong toÃĄn háŧc, tášp háŧĢp sáŧ háŧŊu táŧ là máŧt tášp háŧĢp bao gáŧm tášĨt cášĢ cÃĄc sáŧ cÃģ tháŧ biáŧu diáŧ n dÆ°áŧi dᚥng phÃĒn sáŧ, váŧi táŧ sáŧ và mášŦu sáŧ Äáŧu là sáŧ nguyÊn. Tášp háŧĢp sáŧ háŧŊu táŧ là máŧt trong nháŧŊng khÃĄi niáŧm cÆĄ bášĢn và quan tráŧng trong lÄĐnh váŧąc sáŧ háŧc, Äáš·c biáŧt là trong Äᚥi sáŧ. Hiáŧu vÃ ÃĄp dáŧĨng tášp háŧĢp sáŧ háŧŊu táŧ là rášĨt quan tráŧng trong cÃĄc bà i toÃĄn liÊn quan Äášŋn phÃĒn sáŧ, phÆ°ÆĄng trÃŽnh, Äᚥi sáŧ tuyášŋn tÃnh, v.v. Bà i viášŋt nà y sáš― giášĢi thÃch chi tiášŋt váŧ tášp háŧĢp sáŧ háŧŊu táŧ, cÃĄch biáŧu diáŧ n sáŧ háŧŊu táŧ, tÃnh chášĨt cáŧ§a tášp háŧĢp sáŧ háŧŊu táŧ vÃ ÃĄp dáŧĨng chÚng và o cÃĄc bà i toÃĄn tháŧąc tášŋ.
1. Sáŧ háŧŊu táŧ là gÃŽ?
Sáŧ háŧŊu táŧ là cÃĄc sáŧ x cÃģ tháŧ biáŧu diáŧ n dÆ°áŧi dᚥng phÃĒn sáŧ \(\frac{a}{b}\) , trong ÄÃģ a và b là cÃĄc sáŧ nguyÊn váŧi b khÃĄc 0.
ChÚ Ã―:Â
Sáŧ 0 khÃīng phášĢi là sáŧ háŧŊu táŧ ÃĒm và cÅĐng khÃīng phášĢi là sáŧ háŧŊu táŧ dÆ°ÆĄng.
VÃ dáŧĨ:Â
CÃĄc sáŧ \(\frac{8}{18}\), \(\frac{2}{5}\), \(\frac{8}{3}\), \(\frac{6}{5}\)là cÃĄc sáŧ háŧŊu táŧ.
Tášp háŧĢp cÃĄc sáŧ háŧŊu táŧ ÄÆ°áŧĢc kà hiáŧu là Q.
Ta cÃģ:
Q = {\(\frac{a}{b}\); a, b ⎠Z; b â 0}
Trong ÄÃģ Z là tášp háŧĢp sáŧ tháŧąc.
VÃ dáŧĨ:
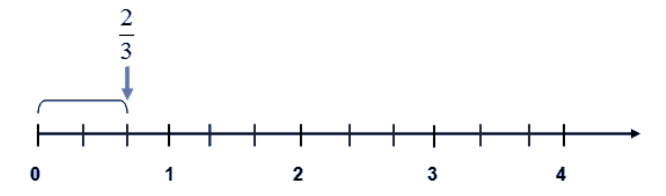
Biáŧu diáŧ n sáŧ háŧŊu táŧ \(\frac{2}{3}\) trÊn tia sáŧ:
2. TÃnh chášĨt cáŧ§a sáŧ háŧŊu táŧ
Tášp háŧĢp sáŧ háŧŊu táŧ là tášp háŧĢp Äášŋm ÄÆ°áŧĢc.
PhÃĐp nhÃĒn sáŧ háŧŊu táŧ cÃģ dᚥng:\(\frac{a}{b} \times \frac{c}{d} =\frac{a\ \times \ c}{b\ \times \ d}\)
VÃ dáŧĨ:
\(\frac{4}{5} \times \frac{3}{2} =\frac{4\ \times \ 3}{5\ \times \ 2} =\frac{12}{10} =\frac{6}{5}\)
PhÃĐp chia sáŧ háŧŊu táŧ cÃģ dᚥng: \(\frac{a}{b} \ :\ \frac{c}{d} =\frac{a\ \times \ d}{b\ \times \ c}\)
VÃ dáŧĨ:
\(\frac{5}{7} \ :\ \frac{2}{3} =\frac{5\ \times \ 3}{7\ \times \ 2} =\frac{15}{14}\)
Nášŋu sáŧ háŧŊu táŧ là sáŧ háŧŊu táŧ dÆ°ÆĄng thÃŽ sáŧ Äáŧi cáŧ§a nÃģ là sáŧ háŧŊu táŧ ÃĒm và ngÆ°áŧĢc lᚥi. TáŧĐc táŧng sáŧ háŧŊu táŧ và sáŧ Äáŧi cáŧ§a nÃģ bášąng 0.
VÃ dáŧĨ:
Sáŧ Äáŧi cáŧ§a sáŧ háŧŊu táŧ dÆ°ÆĄng \(\frac{5}{7}\) là sáŧ háŧŊu táŧ ÃĒm \(-\frac{15}{14}\)
Táŧng hai sáŧ bášąng: \(\frac{5}{7} +\left( -\frac{5}{7}\right) =0\)
3. Sáŧ vÃī táŧ là gÃŽ?
Sáŧ vÃī táŧ là cÃĄc sáŧ viášŋt ÄÆ°áŧĢc dÆ°áŧi dᚥng sáŧ thášp phÃĒn vÃī hᚥn khÃīng tuᚧn hoà n. Trong toÃĄn háŧc, sáŧ vÃī táŧ là sáŧ tháŧąc khÃīng phášĢi là sáŧ háŧŊu táŧ, nghÄĐa là khÃīng tháŧ biáŧu diáŧ n ÄÆ°áŧĢc dÆ°áŧi dᚥng táŧ sáŧ \(\frac{a}{b}\) (và a, b là cÃĄc sáŧ nguyÊn).
VÃ dáŧĨ:Â
- CÄn bášc hai cáŧ§a 2: â2 = 1.4142135623âĶ là máŧt sáŧ vÃī táŧ
- Sáŧ 3,74599âĶ là máŧt sáŧ vÃī táŧ
- Sáŧ vÃī táŧ: 0,1010010001000010000010000001âĶ (ÄÃĒy là sáŧ thášp phÃĒn vÃī hᚥn khÃīng tuᚧn hoà n)
- Sáŧ pi (Ï): 3,14159 26535 89793 23846 26433 83279 50 288âĶ là máŧt sáŧ vÃī táŧ.
Tášp háŧĢp sáŧ vÃī táŧ ÄÆ°áŧĢc kà hiáŧu là : I
TÃnh chášĨt sáŧ vÃī táŧ:
Tášp háŧĢp sáŧ vÃī táŧ là tášp háŧĢp khÃīng Äášŋm ÄÆ°áŧĢc.
4. Sáŧą khÃĄc nhau giáŧŊa sáŧ háŧŊu táŧ và sáŧ vÃī táŧ
Sáŧ háŧŊu táŧ là sáŧ Äášŋm ÄÆ°áŧĢc, cÃēn sáŧ vÃī táŧ là sáŧ khÃīng Äášŋm ÄÆ°áŧĢc.
Sáŧ háŧŊu táŧ cháŧ là phÃĒn sáŧ, cÃēn sáŧ vÃī táŧ cÃģ rášĨt nhiáŧu loᚥi sáŧ khÃĄc nhau.
Sáŧ háŧŊu táŧ bao gáŧm sáŧ thášp phÃĒn vÃī hᚥn tuᚧn hoà n, cÃēn sáŧ vÃī táŧ là cÃĄc sáŧ thášp phÃĒn vÃī hᚥn khÃīng tuᚧn hoà n.
