Cộng, trừ phân số

Trong các bài toán liên quan đến phép cộng và trừ phân số, chúng ta cần phải quy đồng mẫu số các phân số trước khi thực hiện phép tính. Quá trình quy đồng mẫu số được thực hiện bằng cách nhân hoặc chia cả tử và mẫu của các phân số với các số nguyên dương sao cho các phân số đều có cùng mẫu số. Trong bài viết này, chúng ta sẽ tìm hiểu về cách cộng và trừ phân số, quy đồng mẫu số và các ví dụ minh họa để giúp bạn hiểu rõ hơn về phép tính quan trọng này.
1. Phép cộng phân số
a) Cộng hai phân số cùng mẫu
Muốn cộng hai phân số cùng mẫu, ta cộng các tử và giữ nguyên mẫu.
\(\mathrm{\frac{\mathrm{a}}{m}} +\mathrm{\frac{b}{m} =\frac{a+b}{m}} \ \mathrm{( m\ \#\ 0)}\)
Ví dụ:
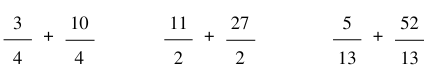
Thực hiện phép tính:
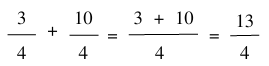
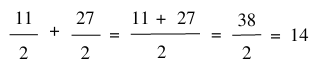
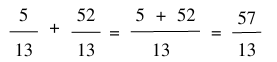
b) Cộng hai phân số khác mẫu
Muốn cộng hai phân số khác mẫu, ta thực hiện quy đồng hai phân số để có một mẫu chung rồi thực hiện cộng các tử với nhau, giữ nguyên mẫu chung.
Ví dụ:
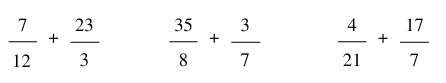
Quy đồng mẫu số và thực hiện phép tính:
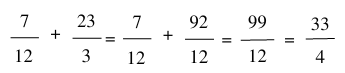
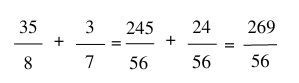
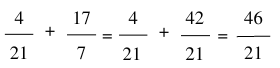
2. Tính chất của phép cộng phân số
Tính chất giao hoán:
Khi đổi chỗ các phân số trong một tổng thì tổng của chúng không thay đổi.
\(\mathrm{\frac{a}{b}} +\mathrm{\frac{c}{d} =\frac{c}{d}} +\mathrm{\frac{a}{b}}\)
Tính chất kết hợp:
Khi cộng một tổng hai phân số với phân số thứ ba thì ta có thể cộng phân số thứ nhất với tổng của hai phân số còn lại.
\(\mathrm{\left(\frac{a}{b} +\frac{c}{d}\right) +\frac{m}{n} =\frac{a}{b} +\left(\frac{c}{d} \ +\frac{m}{n}\right)}\)
Cộng với số 0:
Phân số nào cộng với 0 cũng bằng chính phân số đó.
\(\mathrm{\frac{a}{b} +0=\frac{a}{b}}\)
Ví dụ:
Tính chất giao hoán:
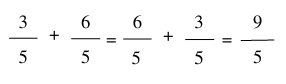
Tính chất kết hợp:
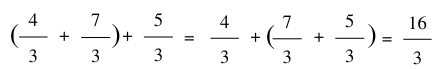
Cộng với số 0:
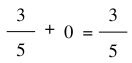
3. Phép trừ phân số
a) Trừ hai phần số cùng mẫu
Muốn trừ hai phân số cùng mẫu ta lấy tử của phân số thứ nhất trừ đi tử của phân số thứ hai và giữ nguyên mẫu.
\(\mathrm{\frac{a}{b} -\frac{c}{b} =\frac{a\ -\ c}{b} \ ( b\ \#\ 0)}\)
Ví dụ:
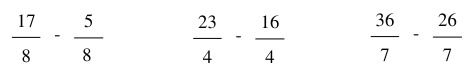
Thực hiện phép tính:
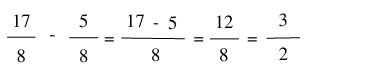
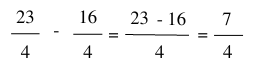
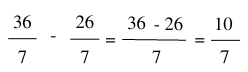
b) Trừ hai phân số khác mẫu
Muốn trừ hai phân số khác mẫu, ta quy đồng hai phân số, rồi trừ hai phân số đó.
Ví dụ:
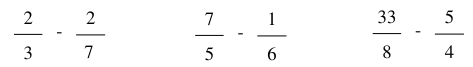
Thực hiện phép tính:
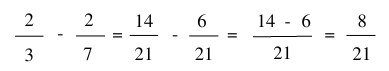
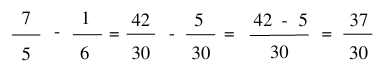
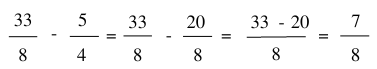
4. Bài tập
Tính giá trị các biểu thức
a) \(\mathrm{\frac{23}{5} +\frac{14}{5} -\frac{10}{5}}\)
b) \(\mathrm{\frac{2}{7} +\frac{4}{7} +\frac{1}{7}}\)
c) \(\mathrm{\frac{2}{9} +\frac{14}{3}}\)
d) \(\mathrm{\frac{31}{2} -\frac{11}{4}}\)
Hướng dẫn:
a) \(\mathrm{\frac{23}{5} +\frac{14}{5} -\frac{10}{5}}\)
\(\mathrm{\frac{23}{5} +\frac{14}{5} -\frac{10}{5}}\) = \(\frac{23}{5} +\frac{14}{5} -\frac{10}{5} =\frac{23+14-10}{5} =\frac{37-10}{5} =\frac{27}{5}\)
b) \(\mathrm{\frac{2}{7} +\frac{4}{7} +\frac{1}{7}}\)
\(\frac{2}{7} +\frac{4}{7} +\frac{1}{7} =\frac{2+4+1}{7} =\frac{7}{7} =1\)
c) \(\mathrm{\frac{2}{9} +\frac{14}{3}}\)
\(\frac{2}{9} +\frac{14}{3} =\frac{2}{9} +\frac{42}{9} =\frac{2+42}{9} =\frac{44}{9}\)
d) \(\mathrm{\frac{31}{2} -\frac{11}{4}}\)
\(\frac{31}{2} -\frac{11}{4} =\frac{62}{4} -\frac{11}{4} =\frac{62-11}{4} =\frac{51}{4}\)
