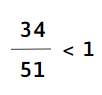PhÃĒn sáŧ và phÃĐp chia sáŧ táŧą nhiÊn
PhÃĒn sáŧ và phÃĐp chia sáŧ táŧą nhiÊn là hai khÃĄi niáŧm cÄn bášĢn trong toÃĄn háŧc, ÄÆ°áŧĢc sáŧ dáŧĨng trong nhiáŧu lÄĐnh váŧąc khÃĄc nhau. PhÃĒn sáŧ là máŧt cÃĄch biáŧu diáŧ n máŧt phᚧn cáŧ§a máŧt sáŧ, cÃģ dᚥng a/b váŧi a và b là hai sáŧ nguyÊn khÃĄc khÃīng. Trong khi ÄÃģ, phÃĐp chia sáŧ táŧą nhiÊn là phÃĐp tÃnh ÄÆ°áŧĢc sáŧ dáŧĨng Äáŧ chia máŧt sáŧ cho máŧt sáŧ khÃĄc, Äáŧ tÃŽm ra sáŧ lÆ°áŧĢng cÃĄc phᚧn bášąng nhau mà chÚng ta cÃģ tháŧ tᚥo ra táŧŦ sáŧ ban Äᚧu. DÃđ ÄÃĒy là hai khÃĄi niáŧm cÆĄ bášĢn, nhÆ°ng chÚng cÃģ tháŧ ÄÆ°áŧĢc sáŧ dáŧĨng Äáŧ giášĢi quyášŋt nháŧŊng vášĨn Äáŧ pháŧĐc tᚥp trong toÃĄn háŧc và cášĢ trong cuáŧc sáŧng hà ng ngà y. Trong bà i viášŋt nà y, chÚng ta sáš― Äi sÃĒu và o khÃĄi niáŧm phÃĒn sáŧ và phÃĐp chia sáŧ táŧą nhiÊn, và tÃŽm hiáŧu cÃĄch sáŧ dáŧĨng chÚng trong cÃĄc bà i toÃĄn tháŧąc tášŋ.
PhÃĒn sáŧ và phÃĐp chia sáŧ táŧą nhiÊn
PhÃĒn sáŧ
PhÃĒn sáŧ là máŧt cÃĄch biáŧu diáŧ n máŧt phᚧn cáŧ§a máŧt sáŧ, ÄÆ°áŧĢc kÃ― hiáŧu dÆ°áŧi dᚥng \(\mathrm{\frac{a}{b}}\), trong ÄÃģ a và b là hai sáŧ nguyÊn khÃĄc khÃīng và b khÃĄc 0.
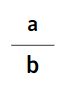
Sáŧ a ÄÆ°áŧĢc gáŧi là táŧ sáŧ, sáŧ b ÄÆ°áŧĢc gáŧi là mášŦu sáŧ. PhÃĒn sáŧ \(\mathrm{\frac{a}{b}}\) biáŧu tháŧ phᚧn cáŧ§a sáŧ báŧ chia ÄÆ°áŧĢc chia thà nh b phᚧn bášąng nhau, máŧi phᚧn cÃģ giÃĄ tráŧ a.
VÃ dáŧĨ:
PhÃĒn sáŧ \(\mathrm{\frac{2}{5}}\) biáŧu tháŧ 2 phᚧn cáŧ§a sáŧ 5 ÄÆ°áŧĢc chia thà nh 5 phᚧn bášąng nhau, máŧi phᚧn cÃģ giÃĄ tráŧ 2.
PhÃĒn sáŧ cÃēn cÃģ tháŧ ÄÆ°áŧĢc rÚt gáŧn bášąng cÃĄch chia táŧ sáŧ và mášŦu sáŧ cho máŧt Æ°áŧc chung cáŧ§a chÚng.
VÃ dáŧĨ:
PhÃĒn sáŧ \(\mathrm{\frac{4}{8}}\) cÃģ tháŧ ÄÆ°áŧĢc rÚt gáŧn thà nh phÃĒn sáŧ \(\mathrm{\frac{1}{2}}\) bášąng cÃĄch chia cášĢ táŧ sáŧ và mášŦu sáŧ cho 4, máŧt Æ°áŧc chung cáŧ§a chÚng.
PhÃĒn sáŧ nháŧ hÆĄn 1
PhÃĒn sáŧ nháŧ hÆĄn 1 là phÃĒn sáŧ mà táŧ sáŧ nháŧ hÆĄn mášŦu sáŧ. Và dáŧĨ: phÃĒn sáŧ \(\mathrm{\frac{2}{3}}\) và phÃĒn sáŧ \(\mathrm{\frac{7}{8}}\) Äáŧu là phÃĒn sáŧ nháŧ hÆĄn 1.
Khi phÃĒn sáŧ nháŧ hÆĄn 1 ÄÆ°áŧĢc biáŧu diáŧ n dÆ°áŧi dᚥng thášp phÃĒn, giÃĄ tráŧ cáŧ§a nÃģ sáš― nášąm trong khoášĢng táŧŦ 0 Äášŋn 1. Và dáŧĨ: phÃĒn sáŧ \(\mathrm{\frac{2}{3}}\) biáŧu diáŧ n dÆ°áŧi dᚥng thášp phÃĒn là 0.6666..., giÃĄ tráŧ nà y nášąm trong khoášĢng táŧŦ 0 Äášŋn 1.
PhÃĒn sáŧ nháŧ hÆĄn 1 cÃģ nhiáŧu áŧĐng dáŧĨng trong toÃĄn háŧc và cuáŧc sáŧng hà ng ngà y, chášģng hᚥn nhÆ° biáŧu diáŧ n táŧ· láŧ phᚧn trÄm, sáŧ lÆ°áŧĢng phᚧn trÄm giášĢm,...
PhÃĒn sáŧ láŧn hÆĄn 1
PhÃĒn sáŧ láŧn hÆĄn 1 là phÃĒn sáŧ mà táŧ sáŧ láŧn hÆĄn mášŦu sáŧ. Và dáŧĨ, phÃĒn sáŧ \(\mathrm{\frac{5}{3}}\) và phÃĒn sáŧ \(\mathrm{\frac{13}{4}}\) Äáŧu là phÃĒn sáŧ láŧn hÆĄn 1.
Khi phÃĒn sáŧ láŧn hÆĄn 1 ÄÆ°áŧĢc biáŧu diáŧ n dÆ°áŧi dᚥng thášp phÃĒn, giÃĄ tráŧ cáŧ§a nÃģ sáš― láŧn hÆĄn 1. Và dáŧĨ, phÃĒn sáŧ \(\mathrm{\frac{5}{3}}\) biáŧu diáŧ n dÆ°áŧi dᚥng thášp phÃĒn là 1.6666..., giÃĄ tráŧ nà y láŧn hÆĄn 1.
PhÃĒn sáŧ láŧn hÆĄn 1 cÅĐng cÃģ nhiáŧu áŧĐng dáŧĨng trong toÃĄn háŧc và cuáŧc sáŧng hà ng ngà y, chášģng hᚥn nhÆ° biáŧu diáŧ n táŧ· láŧ phᚧn trÄm tÄng, sáŧ lÆ°áŧĢng phᚧn trÄm tÄng,...
Viášŋt thÆ°ÆĄng cáŧ§a phÃĐp chia dÆ°áŧi dᚥng phÃĒn sáŧ
PhÃĐp chia hai sáŧ nguyÊn a và b (váŧi b khÃĄc 0) cÃģ tháŧ ÄÆ°áŧĢc biáŧu diáŧ n dÆ°áŧi dᚥng phÃĒn sáŧ:
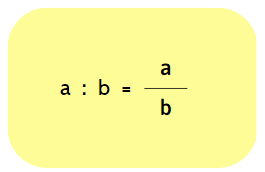
Trong phÃĒn sáŧ nà y, a là sáŧ báŧ chia và b là sáŧ chia. CáŧĨ tháŧ, phÃĒn sáŧ \(\mathrm{\frac{a}{b}}\) cÃģ giÃĄ tráŧ bášąng kášŋt quášĢ cáŧ§a phÃĐp chia a cho b.
VÃ dáŧĨ:
phÃĐp chia 7 cho 3 cÃģ tháŧ ÄÆ°áŧĢc biáŧu diáŧ n dÆ°áŧi dᚥng phÃĒn sáŧ \(\mathrm{\frac{7}{3}}\), trong ÄÃģ 7 là sáŧ báŧ chia và 3 là sáŧ chia. GiÃĄ tráŧ cáŧ§a phÃĒn sáŧ \(\mathrm{\frac{7}{3}}\) là kášŋt quášĢ cáŧ§a phÃĐp chia 7 cho 3, táŧĐc là 2 và phᚧn dÆ° 1.
PhÃĒn sáŧ \(\mathrm{\frac{a}{b}}\) cÃēn ÄÆ°áŧĢc gáŧi là phÃĒn sáŧ thášp phÃĒn và cÃģ tháŧ ÄÆ°áŧĢc biáŧu diáŧ n dÆ°áŧi dᚥng thášp phÃĒn vÃī hᚥn tuᚧn hoà n hoáš·c khÃīng tuᚧn hoà n.
VÃ dáŧĨ:
phÃĒn sáŧ \(\mathrm{\frac{1}{3}}\) cÃģ giÃĄ tráŧ thášp phÃĒn là 0.3333..., là máŧt thášp phÃĒn vÃī hᚥn tuᚧn hoà n, trong khi phÃĒn sáŧ \(\mathrm{\frac{1}{2}}\) cÃģ giÃĄ tráŧ thášp phÃĒn là 0.5, là máŧt thášp phÃĒn khÃīng tuᚧn hoà n.
LÆ°u Ã―:
- Máŧi sáŧ táŧą nhiÊn cÃģ tháŧ viášŋt thà nh máŧt phÃĒn sáŧ cÃģ táŧ sáŧ là sáŧ táŧą nhiÊn ÄÃģ và mášŦu sáŧ bášąng 1.
- PhÃĒn sáŧ cÃģ táŧ sáŧ láŧn hÆĄn mášŦu sáŧ thÃŽ phÃĒn sáŧ ÄÃģ láŧn hÆĄn 1.
- PhÃĒn sáŧ cÃģ táŧ sáŧ bášąng mášŦu sáŧ thÃŽ phÃĒn sáŧ ÄÃģ bášąng 1.
- PhÃĒn sáŧ cÃģ táŧ sáŧ bÃĐ hÆĄn mášŦu sáŧ thÃŽ phÃĒn sáŧ ÄÃģ bÃĐ hÆĄn 1.
Bà i tášp liÊn quan Äášŋn phÃĒn sáŧ và phÃĐp chia sáŧ táŧą nhiÊn
Bà i 1: Viášŋt thÆ°ÆĄng cáŧ§a phÃĐp chia sau dÆ°áŧi dᚥng phÃĒn sáŧ
a) 3 : 4
b) 21 : 13
c) 5 : 31
d) 9 : 17
ÄÃĄp ÃĄn:
a) 3 : 4
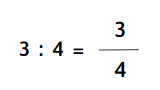
b) 21 : 13
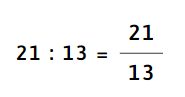
c) 5 : 31
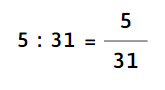
d) 9 : 17
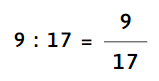
Bà i 2: Viášŋt sáŧ táŧą nhiÊn dÆ°áŧi dᚥng phÃĒn sáŧ cÃģ mášŦu sáŧ là 1
a) 15
b) 7
c) 9
d) 11
ÄÃĄp ÃĄn:
a) 15
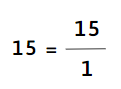
b) 7
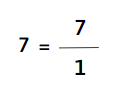
c) 9
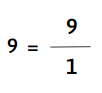
d) 11
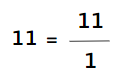
BÃ i 3: So sÃĄnh cÃĄc phÃĒn sáŧ sau váŧi sáŧ 1
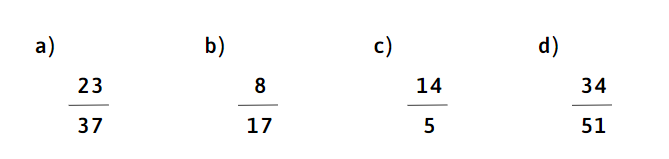
ÄÃĄp ÃĄn:
a)
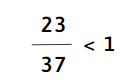
b)
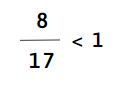
c)
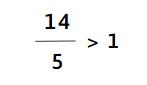
d)