So sánh phân số
Phân số là một khái niệm cơ bản trong toán học, được sử dụng rộng rãi trong nhiều lĩnh vực của cuộc sống hàng ngày. Để giải quyết các bài toán liên quan đến phân phối tài nguyên, chia sẻ chi phí, tính toán tỷ lệ phần trăm và nhiều vấn đề khác, chúng ta cần có khả năng so sánh phân số. Quy tắc so sánh phân số đơn giản và dễ hiểu, tuy nhiên nó vẫn là một trong những khái niệm gây khó khăn đối với nhiều học sinh. Trong bài viết này, chúng ta sẽ cùng tìm hiểu về quy tắc so sánh phân số và áp dụng nó vào một số bài toán cụ thể.
So sánh phân số
Quy tắc so sánh phân số
Để so sánh hai phân số, ta có thể chuyển chúng về cùng mẫu số rồi so sánh tử số của hai phân số đó. Quy tắc so sánh phân số như sau:
a) Nếu cả hai phân số đều có cùng mẫu số, ta so sánh tử số để xác định phân số nào lớn hơn.
- Phân số nào có tử số bé hơn thì phân số đó bé hơn.
- Phân số nào có tử số lớn hơn thì phân số đó lớn hơn.
- Nếu tử số bằng nhau thì hai phân số đó bằng nhau.
Ví dụ:
So sánh phân số \(\mathrm{\frac{2}{5}}\) và \(\mathrm{\frac{4}{5}}\)
Vì cùng mẫu số là 5 nên ta chỉ cần so sánh tử số. \(\mathrm{\frac{4}{5}}\) > \(\mathrm{\frac{2}{5}}\), nên phân số \(\mathrm{\frac{4}{5}}\) lớn hơn phân số \(\mathrm{\frac{2}{5}}\)
b) Nếu hai phân số có khác mẫu số, ta quy đồng mẫu số rồi so sánh tử số.
So sánh phân số \(\mathrm{\frac{1}{2}}\) và \(\mathrm{\frac{3}{4}}\)
Để chuyển chúng về cùng mẫu số, ta nhân mẫu số của \(\mathrm{\frac{1}{2}}\) và \(\mathrm{\frac{3}{4}}\) cho nhau, ta được \(\mathrm{\frac{2}{4}}\) và \(\mathrm{\frac{3}{4}}\).
Vì cùng mẫu số là 4 nên ta so sánh tử số để xác định phân số nào lớn hơn. \(\mathrm{\frac{3}{4}}\) > \(\mathrm{\frac{2}{4}}\), nên phân số \(\mathrm{\frac{3}{4}}\) lớn hơn phân số \(\mathrm{\frac{1}{2}}\).
c) Hai phân số có cùng tử số
- Phân số nào có mẫu số bé hơn thì phân số đó lớn hơn.
- Phân số nào có mẫu số lớn hơn thì phân số đó bé hơn.
- Nếu mẫu số bằng nhau thì hai phân số đó bằng nhau.
Ví dụ:
So sánh phân số \(\mathrm{\frac{4}{9}}\) và \(\mathrm{\frac{4}{7}}\)
Ta so sánh mẫu của hai phân số:
Vì phân số \(\mathrm{\frac{4}{9}}\) có mẫu số lớn hơn mẫu số của phân số \(\mathrm{\frac{4}{7}}\) , 9 > 7, nên \(\mathrm{\frac{4}{7}}\) > \(\mathrm{\frac{4}{9}}\)
d) Chuyển phân số về dạng thập phân và so sánh giá trị của chúng.
So sánh phân số \(\mathrm{\frac{2}{5}}\) và \(\mathrm{\frac{1}{3}}\)
Không thể chuyển chúng về cùng mẫu số, ta chuyển chúng về dạng thập phân:
\(\mathrm{\frac{2}{5}}\) = 0.4 và \(\mathrm{\frac{1}{3}}\) = 0.3333... Ta thấy được rằng 0.4 > 0.3333..., nên phân số \(\mathrm{\frac{2}{5}}\) lớn hơn phân số \(\mathrm{\frac{1}{3}}\).
Bài tập so sánh phân số
Bài 1: So sánh các phân số cùng mẫu
a)
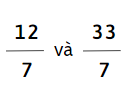
b)
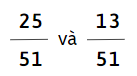
c)
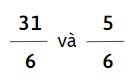
d)
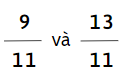
Đáp án:
a)
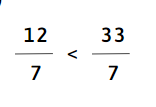
b)
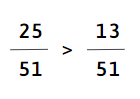
c)
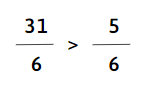
d)
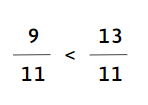
Bài 2: So sánh các phân số khác mẫu
a)
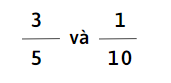
b)
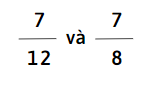
c)
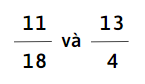
d)
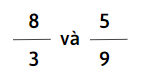
Đáp án:
a) Quy đồng mẫu số:
Mẫu số chung là: 10
\(\frac{3}{5} =\frac{3\times 2}{5\times 2} =\frac{6}{10}\)
Vậy so sánh tử số \(\frac{6}{10}\) và \(\frac{1}{10}\)
Vì 6 > 1 nên \(\frac{6}{10}\) > \(\frac{1}{10}\)
b) Hai phân số có tử số bằng nhau, so sánh mẫu số
Vì 12 > 8, nên phân số \(\frac{7}{12}\) < \(\frac{7}{8}\)
c) Quy đồng mẫu số:
Mẫu số chung nhỏ nhất là 36
\(\frac{11}{18} =\frac{11\times 2}{18\times 2} =\frac{22}{36}\)
\(\frac{13}{4} =\frac{13\times 9}{4\times 9} =\frac{117}{36}\)
So sánh tử số hai mẫu số:
Vì 22 < 117, nên \(\frac{22}{36}\) < \(\frac{117}{36}\)
d) Quy đồng mẫu số:
Mẫu số chung là 9
\(\frac{8}{3} =\frac{8\times 3}{3\times 3} =\frac{24}{9}\)
So sánh tử số hai phân số: \(\frac{24}{9}\)và \(\frac{5}{9}\)
Vì 24 > 5, nên \(\frac{24}{9}\) > \(\frac{5}{9}\)
