Đa giác, đa giác đều

Đa giác là một hình học cơ bản, thú vị và có ứng dụng rộng rãi trong cuộc sống. Việc hiểu rõ về đa giác sẽ giúp chúng ta dễ dàng nhận diện, phân biệt và làm việc với các hình dạng khác nhau trong thực tế, từ kiến trúc, nghệ thuật đến các bài toán toán học phức tạp. Hiểu được đa giác và đa giác đều chính là bước đầu tiên để tiếp cận một cách sâu hơn và toàn diện hơn với thế giới hình học. Có thể nói bài viết này sẽ mang đến bạn một cái nhìn tổng quan nhất, bao gồm các kiến thức về định nghĩa, phân loại, tính chất, công thức tính toán và các bài tập liên quan đến đa giác, đa giác đều.

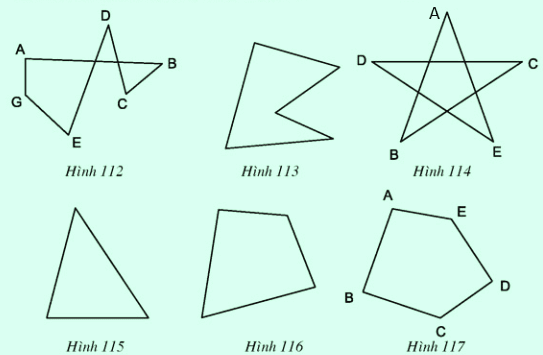
Đa giác là gì? Đặc điểm và phân loại

Đa giác là một hình học phẳng được tạo thành từ một số hữu hạn các đoạn thẳng nối tiếp nhau, sao cho không có hai đoạn thẳng nào cùng nằm trên một đường thẳng, và mỗi điểm chung của hai đoạn thẳng liên tiếp là một đỉnh của đa giác. Nói một cách đơn giản hơn, đa giác là một hình khép kín được tạo thành từ các đoạn thẳng. Các đoạn thẳng này được gọi là cạnh của đa giác, và điểm giao nhau giữa hai cạnh liên tiếp được gọi là đỉnh của đa giác.

Định nghĩa chi tiết về đa giác

Đa giác là một hình học phẳng hai chiều, được xác định bởi một đường gấp khúc khép kín, bao gồm các đoạn thẳng nối tiếp nhau tạo thành một chu trình duy nhất. Mỗi đoạn thẳng này được gọi là một cạnh của đa giác, và điểm giao nhau giữa hai cạnh liên tiếp là một đỉnh. Trong đó:

• Cạnh: Mỗi đoạn thẳng tạo nên đa giác được gọi là cạnh.
• Đỉnh: Điểm giao nhau giữa hai cạnh liên tiếp là một đỉnh.
• Góc: Góc được tạo bởi hai cạnh liên tiếp tại một đỉnh.

Đa giác không phải là một đường cong, mỗi đoạn thẳng của đường biên phải là đường thẳng. Thêm vào đó, đa giác là một hình khép kín, nghĩa là không có điểm bắt đầu hay điểm kết thúc rõ ràng trong chu trình của nó. Việc xác định một hình là đa giác hay không dựa trên việc nó có thỏa mãn tất cả các điều kiện trên hay không.

Đặc điểm cơ bản của đa giác

Đa giác có một số đặc điểm cơ bản sau:

• Hình khép kín: Đa giác luôn là một hình khép kín, có nghĩa là các cạnh nối liền với nhau tạo thành một vòng tròn mà không có điểm đầu hay điểm cuối.
• Số cạnh và số đỉnh: Số cạnh của đa giác luôn bằng số đỉnh. Một đa giác có n cạnh thì cũng có n đỉnh.
• Góc trong: Tổng số đo các góc trong của một đa giác n cạnh là (n-2) * 180 độ.
• Đường chéo: Đường chéo của đa giác là đoạn thẳng nối hai đỉnh không kề nhau. Một đa giác có n cạnh sẽ có n(n-3)/2 đường chéo.

Các đặc điểm này giúp chúng ta phân biệt đa giác với các hình dạng khác. Những đặc điểm này đóng vai trò quan trọng trong việc phân loại và nghiên cứu các tính chất hình học của đa giác.

Phân loại đa giác dựa trên số cạnh

Đa giác được phân loại dựa trên số cạnh của chúng. Dưới đây là một số loại đa giác phổ biến:

• Tam giác: Đa giác có 3 cạnh và 3 đỉnh.
• Tứ giác: Đa giác có 4 cạnh và 4 đỉnh.
• Ngũ giác: Đa giác có 5 cạnh và 5 đỉnh.
• Lục giác: Đa giác có 6 cạnh và 6 đỉnh.
• Thất giác: Đa giác có 7 cạnh và 7 đỉnh.
• Bát giác: Đa giác có 8 cạnh và 8 đỉnh.
• Cửu giác: Đa giác có 9 cạnh và 9 đỉnh.
• Thập giác: Đa giác có 10 cạnh và 10 đỉnh.

Và cứ tiếp tục như vậy, đa giác có thể có bất kỳ số cạnh nào lớn hơn hoặc bằng 3. Việc phân loại đa giác dựa trên số cạnh giúp chúng ta dễ dàng nhận biết và gọi tên chúng một cách chính xác. Mỗi loại đa giác lại có những tính chất và đặc điểm riêng biệt, tạo nên sự đa dạng và phong phú trong thế giới hình học.

Đa giác đều: Khái niệm và ví dụ cụ thể

Đa giác đều là một dạng đặc biệt của đa giác, nổi bật với tính đối xứng hoàn hảo. Đa giác đều là đa giác có tất cả các cạnh bằng nhau và tất cả các góc bằng nhau. Tính chất này tạo nên sự cân đối hoàn hảo, khiến đa giác đều trở nên đặc biệt và được ứng dụng rộng rãi trong nhiều lĩnh vực khác nhau từ kiến trúc, nghệ thuật, đến khoa học và kỹ thuật.

Khái niệm chi tiết về đa giác đều

Đa giác đều là một đa giác mà tất cả các cạnh có cùng độ dài và tất cả các góc trong bằng nhau. Điều này có nghĩa là, trong một đa giác đều, không chỉ các cạnh đều nhau mà các góc tạo ra tại từng đỉnh cũng phải bằng nhau. Ví dụ, một tam giác đều có ba cạnh bằng nhau và ba góc bằng 60 độ, trong khi một hình vuông có bốn cạnh bằng nhau và bốn góc bằng 90 độ.

Đa giác đều có thể có bất kỳ số cạnh nào từ ba trở lên. Mỗi đa giác đều với số cạnh n sẽ có các góc trong bằng nhau và được tính bằng công thức (n-2) * 180° / n. Việc hiểu rõ khái niệm này giúp chúng ta phân biệt giữa đa giác đều và các loại đa giác khác. Sự hoàn hảo trong cấu trúc của đa giác đều không chỉ là một khái niệm toán học mà còn là nguồn cảm hứng trong nghệ thuật và thiết kế.

Tính chất đối xứng của đa giác đều

Đa giác đều sở hữu tính đối xứng rất cao. Mỗi đa giác đều có thể quay quanh tâm của nó một góc nhất định mà vẫn giữ nguyên hình dạng ban đầu. Số lần quay mà đa giác đều vẫn giữ nguyên hình dạng trong một vòng quay đầy đủ (360 độ) chính là số cạnh của nó. Ví dụ, một ngũ giác đều có thể quay 5 lần, mỗi lần 72 độ (360/5), mà vẫn giữ nguyên hình dạng.

Ngoài ra, đa giác đều còn có tính đối xứng qua trục. Mỗi đa giác đều có thể chia thành các phần bằng nhau qua các trục đối xứng đi qua tâm và đỉnh hoặc trung điểm của các cạnh. Số trục đối xứng của một đa giác đều bằng số cạnh nếu số cạnh là lẻ, và bằng gấp đôi số cạnh nếu số cạnh là chẵn. Tính đối xứng này không chỉ làm cho đa giác đều trở nên đẹp mắt mà còn quan trọng trong các ứng dụng thực tế như thiết kế, kiến trúc và nghệ thuật.

Ví dụ cụ thể về các đa giác đều

Dưới đây là một số ví dụ cụ thể về đa giác đều:

• Tam giác đều: Có 3 cạnh bằng nhau và 3 góc bằng nhau (mỗi góc 60 độ). Tam giác đều là đa giác đều đơn giản nhất và có tính đối xứng cao.
• Hình vuông: Có 4 cạnh bằng nhau và 4 góc vuông (mỗi góc 90 độ). Hình vuông là một trường hợp đặc biệt của tứ giác đều và có tính ứng dụng cao trong đời sống.
• Ngũ giác đều: Có 5 cạnh bằng nhau và 5 góc bằng nhau (mỗi góc 108 độ). Ngũ giác đều thường xuất hiện trong các biểu tượng và kiến trúc, chẳng hạn như Lầu Năm Góc của Bộ Quốc phòng Hoa Kỳ.
• Lục giác đều: Có 6 cạnh bằng nhau và 6 góc bằng nhau (mỗi góc 120 độ). Lục giác đều thường thấy trong tự nhiên, ví dụ như cấu trúc của tổ ong, và cũng được sử dụng nhiều trong thiết kế và kiến trúc.

Những ví dụ này minh họa cho sự đa dạng và tính ứng dụng của đa giác đều trong thực tế. Mỗi đa giác đều mang một vẻ đẹp riêng, phản ánh sự cân đối và hài hòa trong toán học cũng như trong cuộc sống.

Lý thuyết về các loại đa giác trong hình học

Đa giác là một trong những khái niệm cơ bản nhất của hình học, và việc hiểu rõ lý thuyết về các loại đa giác là nền tảng quan trọng để tiếp cận các kiến thức hình học phức tạp hơn. Lý thuyết về đa giác không chỉ bao gồm định nghĩa và phân loại mà còn đi sâu vào các tính chất, các định lý và các ứng dụng thực tiễn. Cái hay của lý thuyết về đa giác nằm ở việc nó kết nối chặt chẽ giữa lý thuyết toán học thuần túy và ứng dụng thực tế trong cuộc sống.

Định lý về tổng các góc trong của đa giác

Một trong những định lý quan trọng nhất về đa giác là định lý về tổng các góc trong. Định lý này phát biểu rằng tổng số đo các góc trong của một đa giác n cạnh là (n-2) * 180 độ. Công thức này có thể được chứng minh bằng cách chia đa giác thành (n-2) tam giác, mỗi tam giác có tổng số đo các góc là 180 độ.

Ví dụ, tổng các góc trong của một tam giác (n=3) là (3-2) 180 = 180 độ, của một tứ giác (n=4) là (4-2) 180 = 360 độ, và của một ngũ giác (n=5) là (5-2) * 180 = 540 độ. Định lý này không chỉ là một công cụ toán học quan trọng mà còn giúp chúng ta hiểu rõ hơn về cấu trúc và tính chất của các đa giác khác nhau.

Đường chéo và mối quan hệ giữa số cạnh và đường chéo

Đường chéo của đa giác là đoạn thẳng nối hai đỉnh không kề nhau. Số đường chéo của một đa giác n cạnh có thể được tính bằng công thức n(n-3)/2. Công thức này xuất phát từ việc mỗi đỉnh có thể nối với (n-3) đỉnh khác (trừ chính nó và hai đỉnh kề), và mỗi đường chéo được đếm hai lần (một lần cho mỗi đỉnh mà nó nối).

Ví dụ, một tam giác không có đường chéo nào (3(3-3)/2 = 0), một tứ giác có 2 đường chéo (4(4-3)/2 = 2), và một ngũ giác có 5 đường chéo (5(5-3)/2 = 5). Mối quan hệ giữa số cạnh và số đường chéo cho thấy sự phức tạp tăng lên khi số cạnh của đa giác tăng. Điều này cũng phản ánh sự phong phú và đa dạng trong cấu trúc của các đa giác khác nhau.

Ứng dụng của lý thuyết đa giác trong các bài toán thực tế

Lý thuyết về đa giác không chỉ giới hạn trong sách giáo khoa mà còn có rất nhiều ứng dụng thực tế. Trong kiến trúc, đa giác được sử dụng để thiết kế các tòa nhà, cầu, và các công trình khác. Ví dụ, các kiến trúc sư thường sử dụng các đa giác đều để tạo ra các cấu trúc có tính đối xứng và cân đối, như Lầu Năm Góc ở Hoa Kỳ.

Trong nghệ thuật, đa giác là nguồn cảm hứng cho các tác phẩm hội họa, điêu khắc và thiết kế đồ họa. Các họa sĩ thường sử dụng các đa giác để tạo ra các hình khối và kết cấu trong tác phẩm của mình. Trong khoa học máy tính, đa giác được sử dụng trong đồ họa máy tính để tạo ra các mô hình 3D và trong các thuật toán xử lý hình ảnh.

Những ứng dụng này cho thấy tầm quan trọng của lý thuyết đa giác trong đời sống và các lĩnh vực khác nhau. Việc hiểu rõ lý thuyết này không chỉ giúp chúng ta giải quyết các bài toán toán học mà còn mở ra những khả năng sáng tạo và ứng dụng trong thực tế.

Công thức tính chu vi và diện tích của đa giác

Để hiểu và làm việc với đa giác một cách hiệu quả, việc nắm vững các công thức tính chu vi và diện tích là rất quan trọng. Chu vi của đa giác là tổng độ dài các cạnh, trong khi diện tích là phần không gian mà đa giác đó chiếm giữ trên mặt phẳng. Các công thức này không chỉ hữu ích trong các bài toán học thuật mà còn cần thiết trong nhiều ứng dụng thực tế như xây dựng, thiết kế và đo đạc.

Công thức tính chu vi đa giác

Chu vi của một đa giác là tổng độ dài tất cả các cạnh của nó. Để tính chu vi (P) của một đa giác, ta chỉ cần cộng độ dài của tất cả các cạnh lại với nhau. Công thức tổng quát để tính chu vi của một đa giác n cạnh với độ dài các cạnh là a1, a2, …, an là:

P = a1 + a2 + … + an

Ví dụ, chu vi của một tam giác có các cạnh lần lượt là 3cm, 4cm và 5cm là 3 + 4 + 5 = 12cm. Đối với một tứ giác có các cạnh là 2cm, 3cm, 4cm và 5cm, chu vi sẽ là 2 + 3 + 4 + 5 = 14cm.

Đối với đa giác đều, việc tính chu vi trở nên đơn giản hơn vì tất cả các cạnh đều bằng nhau. Nếu một đa giác đều có n cạnh và mỗi cạnh có độ dài là a, thì chu vi của nó sẽ là:

P = n * a

Ví dụ, chu vi của một hình vuông có cạnh 4cm là 4 4 = 16cm, và chu vi của một lục giác đều có cạnh 5cm là 6 5 = 30cm.

Công thức tính diện tích đa giác đều

Diện tích của đa giác đều có thể được tính bằng nhiều cách khác nhau tùy thuộc vào thông tin đã biết. Một trong những công thức phổ biến nhất để tính diện tích (S) của một đa giác đều n cạnh, mỗi cạnh có độ dài a, và bán kính đường tròn ngoại tiếp R là:

S = (1/2) n a * r

Trong đó r là bán kính đường tròn nội tiếp đa giác đều (apothème), có thể được tính bằng công thức:

r = a / (2 * tan(π/n))

Hoặc, nếu biết bán kính R của đường tròn ngoại tiếp, diện tích có thể được tính bằng công thức:

S = (1/2) n R^2 * sin(2π/n)

Ví dụ, để tính diện tích của một lục giác đều có cạnh 4cm, ta có thể sử dụng công thức trên với n=6 và a=4. Trước hết, tính r:

r = 4 / (2 * tan(π/6)) ≈ 3.464 cm

Sau đó, tính diện tích:

S = (1/2) 6 4 * 3.464 ≈ 41.57 cm²

Công thức tính diện tích đa giác không đều

Đối với đa giác không đều, việc tính diện tích phức tạp hơn và thường yêu cầu chia đa giác thành các tam giác nhỏ hơn. Sau đó, ta tính diện tích của từng tam giác và cộng chúng lại để được diện tích tổng của đa giác.

Một phương pháp phổ biến là sử dụng công thức Heron để tính diện tích tam giác khi biết độ dài ba cạnh. Nếu tam giác có các cạnh a, b, và c, và nửa chu vi p = (a + b + c) / 2, thì diện tích S của tam giác là:

S = √(p (p – a) (p – b) * (p – c))

Ví dụ, để tính diện tích của một tứ giác không đều, ta có thể chia nó thành hai tam giác bằng một đường chéo, tính diện tích của mỗi tam giác bằng công thức Heron, và cộng hai diện tích lại.

Phương pháp chia đa giác không đều thành các tam giác và tính diện tích từng phần là một kỹ thuật quan trọng trong toán học và có nhiều ứng dụng trong thực tế, chẳng hạn như trong việc đo đạc diện tích đất đai không có hình dạng chuẩn.

Các bài tập thực hành về đa giác và giải pháp

Thực hành là cách tốt nhất để hiểu sâu sắc về đa giác. Các bài tập về đa giác không chỉ giúp củng cố kiến thức lý thuyết mà còn phát triển kỹ năng giải quyết vấn đề và tư duy logic. Dưới đây là một số bài tập thực hành về đa giác kèm theo giải pháp chi tiết, giúp bạn áp dụng các kiến thức đã học vào thực tế.

Bài tập về tính chu vi đa giác

Bài tập 1: Tính chu vi của một ngũ giác có các cạnh lần lượt là 5cm, 7cm, 9cm, 11cm và 13cm.

Giải pháp:

Chu vi của ngũ giác này là tổng độ dài của các cạnh:

P = 5 + 7 + 9 + 11 + 13 = 45cm

Bài tập 2: Một lục giác đều có cạnh dài 8cm. Tính chu vi của lục giác đều đó.

Giải pháp:

Vì lục giác đều có 6 cạnh bằng nhau, chu vi của nó sẽ là:

P = 6 * 8 = 48cm

Bài tập 3: Một mảnh vườn hình chữ nhật có chiều dài 20m và chiều rộng 15m. Người ta muốn rào xung quanh mảnh vườn bằng hàng rào dây thép gai. Hỏi cần bao nhiêu mét dây thép gai để rào kín mảnh vườn?

Giải pháp:

Mảnh vườn hình chữ nhật là một tứ giác. Chu vi của mảnh vườn là:

P = 2 * (20 + 15) = 70m

Vậy cần 70 mét dây thép gai để rào kín mảnh vườn.

Bài tập về tính diện tích đa giác đều

Bài tập 1: Tính diện tích của một ngũ giác đều có cạnh dài 6cm và bán kính đường tròn nội tiếp là 4.13cm.

Giải pháp:

Diện tích của ngũ giác đều có thể được tính bằng công thức:

S = (1/2) n a * r

Với n=5, a=6, và r=4.13, ta có:

S = (1/2) 5 6 * 4.13 = 61.95 cm²

Bài tập 2: Tính diện tích của một tam giác đều có cạnh dài 10cm.

Giải pháp:

Đầu tiên, ta cần tìm chiều cao (h) của tam giác đều. Trong tam giác đều, chiều cao cũng là đường trung tuyến và đường phân giác, chia tam giác thành hai tam giác vuông bằng nhau. Sử dụng định lý Pythagoras, ta có:

h = √(a² – (a/2)²) = √(10² – 5²) = √(100 – 25) = √75 ≈ 8.66 cm

Diện tích của tam giác đều là:

S = (1/2) a h = (1/2) 10 8.66 ≈ 43.3 cm²

Bài tập 3: Một hình bát giác đều có cạnh 4cm và bán kính đường tròn ngoại tiếp là 5.23cm. Tính diện tích của hình bát giác đều đó.

Giải pháp:

Diện tích của bát giác đều có thể được tính bằng công thức:

S = (1/2) n R² * sin(2π/n)

Với n=8, R=5.23, ta có:

S = (1/2) 8 5.23² * sin(2π/8) ≈ 76.8 cm²

Bài tập về đa giác không đều và ứng dụng thực tế

Bài tập 1: Một mảnh đất hình tứ giác có các cạnh lần lượt là 20m, 25m, 30m và 35m. Đường chéo chia mảnh đất thành hai tam giác có độ dài lần lượt là 40m. Tính diện tích của mảnh đất.

Giải pháp:

Gọi hai tam giác là ABC và ADC với đường chéo AC = 40m. Ta sẽ tính diện tích từng tam giác sử dụng công thức Heron.

Tam giác ABC có a=20, b=25, c=40. Nửa chu vi p = (20+25+40)/2 = 42.5. Diện tích S1 = √(42.5*(42.5-20)(42.5-25)(42.5-40)) ≈ 248.7 m².

Tam giác ADC có a=30, b=35, c=40. Nửa chu vi p = (30+35+40)/2 = 52.5. Diện tích S2 = √(52.5*(52.5-30)(52.5-35)(52.5-40)) ≈ 522.4 m².

Diện tích mảnh đất là S = S1 + S2 ≈ 248.7 + 522.4 = 771.1 m².

Bài tập 2: Một người muốn lát gạch cho một sân hình ngũ giác không đều. Các cạnh của sân lần lượt là 5m, 6m, 7m, 8m và 9m. Người đó chia sân thành ba tam giác để dễ tính toán. Hãy giúp người đó tính diện tích của sân.

Giải pháp:

Để giải bài toán này, ta cần biết thêm thông tin về các đường chéo hoặc góc của ngũ giác. Tuy nhiên, nếu giả sử người đó đã đo đạc và tính được diện tích của ba tam giác lần lượt là 12 m², 15 m² và 18 m², thì diện tích của sân sẽ là tổng diện tích của ba tam giác:

S = 12 + 15 + 18 = 45 m²

Những bài tập này cho thấy cách áp dụng kiến thức về đa giác vào các tình huống thực tế, từ việc tính chu vi hàng rào đến việc đo đạc diện tích đất đai. Việc thực hành các bài tập này không chỉ giúp củng cố kiến thức mà còn phát triển kỹ năng giải quyết vấn đề trong cuộc sống hàng ngày.

Tìm hiểu về đa giác lồi và đa giác lõm

Trong thế giới của đa giác, chúng ta không chỉ gặp các đa giác có hình dạng đều đặn mà còn có những đa giác với hình thù phức tạp hơn, được phân loại thành đa giác lồi và đa giác lõm. Việc phân biệt hai loại đa giác này dựa trên tính chất của các góc trong và đường chéo của chúng. Hiểu rõ về đa giác lồi và đa giác lõm không chỉ quan trọng trong lý thuyết hình học mà còn cần thiết trong các ứng dụng thực tế như thiết kế đồ họa, xử lý ảnh và tối ưu hóa.

Định nghĩa và đặc điểm của đa giác lồi

Đa giác lồi là đa giác mà tất cả các góc trong của nó đều nhỏ hơn 180 độ. Điều này có nghĩa là, nếu ta vẽ một đoạn thẳng nối bất kỳ hai điểm nào nằm trong hoặc trên biên của đa giác, đoạn thẳng đó sẽ hoàn toàn nằm trong đa giác. Một cách khác để nhận biết đa giác lồi là tất cả các đường chéo của nó đều nằm hoàn toàn bên trong đa giác.

Ví dụ, tất cả các đa giác đều như tam giác đều, hình vuông, ngũ giác đều đều là đa giác lồi. Các tứ giác lồi như hình chữ nhật, hình bình hành, hình thoi cũng là những ví dụ điển hình của đa giác lồi.

Đa giác lồi có một số tính chất quan trọng:

• Tổng các góc trong của một đa giác lồi n cạnh là (n-2) * 180 độ.
• Mỗi góc ngoài của đa giác lồi đều nhỏ hơn 180 độ.
• Đường thẳng đi qua một cạnh của đa giác lồi chia mặt phẳng thành hai nửa, và đa giác lồi nằm hoàn toàn về một phía của đường thẳng đó.

Định nghĩa và đặc điểm của đa giác lõm

Đa giác lõm là đa giác có ít nhất một góc trong lớn hơn 180 độ. Điều này dẫn đến việc nếu ta vẽ một đoạn thẳng nối hai điểm bất kỳ trong đa giác, có thể có phần của đoạn thẳng đó nằm ngoài đa giác. Một cách khác để nhận biết đa giác lõm là có ít nhất một đường chéo nằm bên ngoài đa giác.

Ví dụ, một hình ngôi sao năm cánh là một đa giác lõm vì nó có các góc nhọn hướng vào trong, tạo thành các góc lớn hơn 180 độ. Một tứ giác có một góc lõm (lớn hơn 180 độ) cũng là một đa giác lõm.

Đa giác lõm có các đặc điểm sau:

• Tổng các góc trong của một đa giác lõm n cạnh vẫn là (n-2) * 180 độ, giống như đa giác lồi.
• Có ít nhất một góc ngoài lớn hơn 180 độ.
• Có ít nhất một đường chéo nằm bên ngoài đa giác.

Ứng dụng và ý nghĩa của việc phân biệt đa giác lồi và đa giác lõm

Việc phân biệt giữa đa giác lồi và đa giác lõm không chỉ quan trọng trong lý thuyết hình học mà còn có nhiều ứng dụng thực tế. Trong đồ họa máy tính, việc xác định một đa giác là lồi hay lõm giúp tối ưu hóa các thuật toán tô màu, xử lý va chạm và hiển thị hình ảnh. Đa giác lồi thường dễ xử lý hơn đa giác lõm trong các thuật toán này.

Trong lĩnh vực tối ưu hóa, các bài toán liên quan đến đa giác lồi thường dễ giải quyết hơn so với đa giác lõm. Ví dụ, bài toán tìm bao lồi (convex hull) của một tập hợp điểm – tức là tìm đa giác lồi nhỏ nhất chứa tất cả các điểm – có nhiều ứng dụng trong nhận dạng mẫu, thị giác máy tính và các lĩnh vực khác.

Trong kiến trúc và thiết kế, việc sử dụng đa giác lồi và đa giác lõm có thể tạo ra các hình dạng và không gian thú vị. Đa giác lồi thường mang lại cảm giác ổn định và cân đối, trong khi đa giác lõm có thể tạo ra các không gian động và phức tạp hơn.

Hiểu rõ về đa giác lồi và đa giác lõm giúp chúng ta không chỉ nắm vững kiến thức hình học mà còn có thể áp dụng chúng vào nhiều lĩnh vực khác nhau, từ nghệ thuật, thiết kế đến khoa học máy tính và tối ưu hóa.

Kiểm tra kiến thức về đa giác qua bài tập trắc nghiệm

Để kiểm tra và củng cố kiến thức về đa giác, không gì hiệu quả hơn là làm các bài tập trắc nghiệm. Các câu hỏi trắc nghiệm giúp bạn ôn tập lại các khái niệm, định nghĩa, công thức và tính chất của đa giác một cách nhanh chóng và chính xác. Dưới đây là một số câu hỏi trắc nghiệm về đa giác kèm theo đáp án, giúp bạn tự đánh giá mức độ hiểu biết của mình.

Câu hỏi trắc nghiệm về định nghĩa và phân loại đa giác

Câu 1: Đa giác là hình như thế nào?

1. Hình có ít nhất 3 cạnh

2. Hình khép kín tạo bởi các đoạn thẳng

3. Hình có các cạnh bằng nhau

4. Hình có các góc bằng nhau

Đáp án: B

Câu 2: Đa giác nào sau đây không phải là đa giác đều?

1. Tam giác đều

2. Hình vuông

3. Hình chữ nhật

4. Lục giác đều

Đáp án: C

Câu 3: Đa giác có 7 cạnh được gọi là gì?

1. Thất giác

2. Bát giác

3. Lục giác

4. Cửu giác

Đáp án: A

Câu 4: Một đa giác có tổng các góc trong bằng 540 độ. Đa giác đó có bao nhiêu cạnh?

1. 4

2. 5

3. 6

4. 7

Đáp án: B

Giải thích: Tổng các góc trong của đa giác n cạnh là (n-2) 180 độ. Ta có (n-2) 180 = 540 => n – 2 = 3 => n = 5.

Câu hỏi trắc nghiệm về đa giác lồi và đa giác lõm

Câu 1: Đa giác lồi là đa giác có đặc điểm gì?

1. Có ít nhất một góc lớn hơn 180 độ

2. Có tất cả các góc nhỏ hơn 180 độ

3. Có ít nhất một đường chéo nằm ngoài đa giác

4. Có các cạnh không bằng nhau

Đáp án: B

Câu 2: Đa giác nào sau đây là đa giác lõm?

1. Hình bình hành

2. Hình thoi

3. Hình thang cân

4. Hình ngôi sao

Đáp án: D

Câu 3: Trong đa giác lõm, khẳng định nào sau đây là đúng?

1. Tất cả các đường chéo đều nằm trong đa giác

2. Có ít nhất một đường chéo nằm ngoài đa giác

3. Tất cả các góc đều nhỏ hơn 180 độ

4. Không có góc nào lớn hơn 180 độ

Đáp án: B

Câu 4: Một tứ giác có một góc bằng 200 độ. Tứ giác đó là đa giác gì?

1. Đa giác lồi

2. Đa giác lõm

3. Hình chữ nhật

4. Hình vuông

Đáp án: B

Câu hỏi trắc nghiệm về chu vi và diện tích đa giác

Câu 1: Chu vi của đa giác được tính như thế nào?

1. Nhân độ dài các cạnh với nhau

2. Cộng độ dài tất cả các cạnh

3. Chia độ dài cạnh cho số cạnh

4. Bình phương độ dài cạnh

Đáp án: B

Câu 2: Một ngũ giác đều có cạnh dài 5cm. Chu vi của nó là bao nhiêu?

1. 10cm

2. 15cm

3. 20cm

4. 25cm

Đáp án: D

Giải thích: Chu vi của ngũ giác đều là 5 * 5 = 25cm.

Câu 3: Diện tích của tam giác đều có cạnh 6cm là bao nhiêu?

1. 9√3 cm²

2. 18 cm²

3. 36 cm²

4. 12√3 cm²

Đáp án: A

Giải thích: Chiều cao của tam giác đều là h = √(6² – 3²) = √27 = 3√3 cm. Diện tích là S = (1/2) 6 3√3 = 9√3 cm².

Câu 4: Một hình vuông có diện tích 64 cm². Cạnh của hình vuông đó dài bao nhiêu?

1. 4 cm

2. 8 cm

3. 16 cm

4. 32 cm

Đáp án: B

Giải thích: Cạnh của hình vuông là √64 = 8 cm.

Những câu hỏi trắc nghiệm này giúp bạn ôn tập và kiểm tra kiến thức về đa giác, đa giác đều một cách toàn diện, từ định nghĩa, phân loại, tính chất đến các công thức tính toán. Việc thường xuyên làm các bài tập trắc nghiệm sẽ giúp bạn nắm vững kiến thức và tự tin hơn khi gặp các bài toán về đa giác.