Đồ thị của hàm số y = ax² (a ≠ 0)

Trong toán học, hàm số bậc hai y = ax² (a ≠ 0) là một trong những hàm số quan trọng và thường được sử dụng trong các bài toán. Hàm số này có đặc điểm đặc trưng của đường parabol, với hình dạng đặc biệt và rất quen thuộc. Trong bài viết này, chúng ta sẽ cùng tìm hiểu về đồ thị của hàm số y = ax², các đặc điểm quan trọng của nó và cách vẽ đồ thị.

Đồ thị của hàm số y = ax² (a ≠ 0)

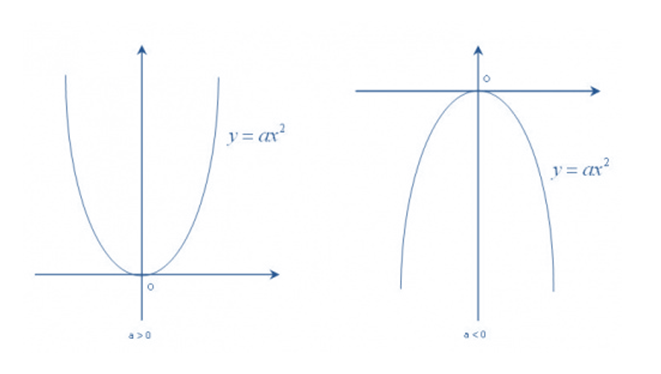
Đồ thị của hàm số y = ax² (a ≠ 0) là một đường parabol với hệ số dương hoặc âm phụ thuộc vào giá trị của a. Khi a > 0, đồ thị của hàm số mở lên trên và có đáy tại điểm (0,0). Khi a < 0, đồ thị của hàm số mở xuống dưới và cũng có đáy tại điểm (0,0).

Hình dạng của đồ thị phụ thuộc vào giá trị của a và đỉnh của parabol nằm trên trục y tại điểm (0,0). Nếu a > 0, đỉnh sẽ là điểm có tọa độ (0,0) và đồ thị mở lên, còn nếu a < 0, đỉnh sẽ là điểm có tọa độ (0,0) và đồ thị mở xuống

.

Đặc điểm của đồ thị hàm số y = ax²:

• Đối xứng qua trục tung: Đồ thị của hàm số y = ax² là đối xứng qua trục tung, có nghĩa là nếu điểm (x,y) nằm trên đồ thị, thì điểm (-x,y) cũng nằm trên đồ thị.

• Điểm cực đại hoặc cực tiểu: Điểm cực đại hoặc cực tiểu của đồ thị là điểm trên đường cong đồ thị nằm ở đỉnh của đường parabol. Điểm cực đại nằm ở đỉnh của đường parabol mở xuống, còn điểm cực tiểu nằm ở đỉnh của đường parabol mở lên. Điểm đỉnh của đường parabol là điểm (0,0).

• Đường tiệm cận: Hàm số y = ax² không có đường tiệm cận vì khi x tiến đến vô cùng hoặc âm vô cùng, giá trị của hàm số cũng tăng lên vô hạn dương.

• Phương trình trục đối xứng: Trục đối xứng của đồ thị là trục tung đi qua đỉnh của parabol tại điểm (0,0). Phương trình trục đối xứng là x = 0.

• Hướng mở rộng của đồ thị: Nếu a > 0, đồ thị của hàm số y = ax² mở lên, còn nếu a < 0, đồ thị mở xuống.

• Điểm cắt trục Ox: Để tìm điểm cắt trục Ox, ta giải phương trình ax² = 0, ta được x = 0. Do đó, điểm cắt trục Ox là (0,0).

Đường cong parabol

Đường cong parabol là một đường cong được tạo thành bởi một hàm số bậc hai y = ax² (a ≠ 0). Đây là một đường cong quen thuộc và được sử dụng trong nhiều lĩnh vực, từ toán học đến vật lý và kỹ thuật.

Đặc trưng của đường cong parabol là hình dạng cong lõm hoặc lồi, phụ thuộc vào hệ số a trong hàm số y = ax². Nếu a > 0, đường cong parabol lõm xuống và có đỉnh ở trên cùng của đường cong. Nếu a < 0, đường cong parabol lồi lên và có đỉnh ở dưới cùng của đường cong. Đường cong parabol có điểm đối xứng qua trục tung và không có đường tiệm cận.

Ứng dụng của đường cong parabol rất đa dạng. Chẳng hạn, trong vật lý, đường cong parabol thường được sử dụng để mô tả quỹ đạo của vật chuyển động dưới tác động của trọng lực. Trong kỹ thuật, đường cong parabol được áp dụng để thiết kế các hệ thống tập trung ánh sáng, các thiết bị phân tích tín hiệu, hay các bộ lọc tín hiệu. Ngoài ra, đường cong parabol còn được ứng dụng trong các lĩnh vực như địa chất học, kinh tế học, và nhiều lĩnh vực khác.

Đường cong parabol là một khái niệm quan trọng và có ứng dụng rộng trong nhiều lĩnh vực trong thực tế. Dưới đây là một số ví dụ cụ thể về sự xuất hiện của đường cong parabol trong thực tế:

• Quỹ đạo của một vật ném lên trời: Trong vật lý, đường cong parabol được sử dụng để mô tả quỹ đạo của một vật được ném lên trời với vận tốc ban đầu. Nếu ta bỏ qua sự tác động của lực ma sát và giả sử rằng trái đất là một mặt phẳng, quỹ đạo của vật này sẽ có hình dạng là một đường cong parabol.

• Thiết kế hệ thống tập trung ánh sáng: Trong kỹ thuật, đường cong parabol được sử dụng để thiết kế các hệ thống tập trung ánh sáng, chẳng hạn như ống kính của một đèn pin. Với hình dạng của một đường cong parabol, ánh sáng có thể được tập trung tại một điểm tiêu điểm duy nhất.

• Thiết kế các thiết bị phân tích tín hiệu: Đường cong parabol cũng được áp dụng trong thiết kế các thiết bị phân tích tín hiệu, chẳng hạn như máy quét hoặc các ứng dụng trong tín hiệu âm thanh. Với hình dạng của một đường cong parabol, tín hiệu được phân tích có thể được tập trung vào một vị trí cụ thể, giúp cho việc phân tích và xử lý dữ liệu trở nên dễ dàng hơn.

• Kinh tế học: Trong kinh tế học, đường cong parabol cũng được sử dụng để mô tả quá trình tối ưu hóa. Ví dụ, đường cong parabol có thể được sử dụng để mô tả quá trình tối ưu hóa giữa hai biến số, trong đó mục tiêu là đạt được giá trị lớn nhất (hoặc nhỏ nhất) của một hàm số.

Trên đây chỉ là một số ví dụ nhỏ về sự xuất hiện của đường cong parabol trong thực tế. Chúng ta có thể thấy rằng đường cong parabol là một khái niệm quan trọng và có ứng dụng rộng trong nhiều lĩnh vực khác nhau.