Mở rộng phân số. Phân số bằng nhau
Phân số là một khái niệm cơ bản trong toán học, được sử dụng trong nhiều lĩnh vực từ đại số đến hình học. Phân số có thể được mở rộng bằng cách nhân hoặc chia cả tử và mẫu với cùng một số. Tuy nhiên, đôi khi, phân số cần phải được mở rộng bằng các phép tính khác nhau để giải quyết các vấn đề toán học phức tạp. Trong khi đó, hai phân số được coi là bằng nhau nếu chúng có giá trị tương đương, tức là chúng có cùng giá trị khi được rút gọn về dạng tối giản. Trong bài viết này, chúng ta sẽ tìm hiểu thêm về khái niệm mở rộng của phân số và cách xác định hai phân số có bằng nhau hay không.
Mở rộng phân số
Khái niệm phân số:
Phân số là sự biểu diễn số hữu tỷ dưới dạng tỷ lệ của hai số nguyên, trong đó số ở trên được gọi là tử số, còn số ở dưới được gọi là mẫu số. Điều kiện bắt buộc là mẫu số phải khác 0.
Phân số được biểu diễn như sau: \(\frac{a}{b}\)
Trong đó:
- a được gọi là tử số
- b được gọi là mẫu số
Mỗi phân số gồm có 2 phần: tử số và mẫu số. Tử số là số tự nhiên viết trên gạch ngang. Mẫu số là số tự nhiên khác 0 viết dưới dấu gạch ngang.
Với tử số là a và mẫu số là b, b khác 0, a, b là số nguyên.
Mở rộng phân số:
Mở rộng phân số là quá trình nhân hoặc chia cả tử và mẫu với cùng một số để tạo ra một phân số có giá trị tương đương với phân số ban đầu, nhưng có dạng khác nhau. Quá trình mở rộng phân số có thể được sử dụng để giải quyết các bài toán phức tạp hoặc đơn giản chỉ để đưa phân số về dạng tối giản.
Ví dụ:
Để mở rộng phân số \(\frac{3}{4}\), chúng ta có thể nhân cả tử và mẫu với số 2, ta được phân số tương đương \(\frac{6}{8}\) hoặc ta có thể nhân cả tử và mẫu với số 3, ta được phân số tương đương \(\frac{9}{12}\). Tuy nhiên, để đưa phân số về dạng tối giản, chúng ta cần chia cả tử và mẫu cho ước chung lớn nhất (UCLN) của chúng. Vì vậy, phân số \(\frac{6}{8}\) và \(\frac{9}{12}\) đều có thể được rút gọn thành phân số \(\frac{3}{4}\).
Mở rộng phân số cũng có thể áp dụng khi muốn so sánh hai phân số và cần đưa chúng về cùng mẫu số để so sánh. Quá trình này được gọi là tìm mẫu số chung nhỏ nhất.
Tính chất cơ bản của phân số
Phân số có các tính chất cơ bản như sau:
-
Phân số là một cách biểu diễn số hữu tỉ dưới dạng tử và mẫu số.
-
Tử số (số trên) và mẫu số (số dưới) của phân số phải là các số nguyên, và mẫu số phải khác 0.
-
Các phân số có thể được so sánh, cộng, trừ, nhân và chia nhau.
-
Hai phân số tương đương khi và chỉ khi chúng có cùng giá trị sau khi được rút gọn về dạng tối giản.
-
Để rút gọn phân số, ta chia cả tử và mẫu cho ước chung lớn nhất của chúng.
-
Để cộng, trừ, nhân hay chia phân số, ta làm tương tự với phép tính tương ứng trên tử số và mẫu số của chúng.
-
Khi cộng, trừ, nhân hay chia các phân số với nhau, ta có thể cần đưa chúng về cùng mẫu số trước khi thực hiện phép tính.
-
Khi chia phân số cho một số nguyên khác 0, ta nhân mẫu số với số đó để tạo ra phân số tương đương.
-
Khi nhân hai phân số với nhau, ta nhân cả tử và nhân mẫu với nhau.
-
Phân số có thể được biểu diễn dưới dạng số thập phân, với số thập phân là kết quả của phép chia tử số cho mẫu số.
Hai phân số bằng nhau
Hai phân số được gọi là bằng nhau khi chúng có cùng giá trị, tức là tử số và mẫu số của hai phân số đều bằng nhau sau khi được rút gọn về dạng tối giản.
Ví dụ:
Phân số \(\frac{2}{4}\) và \(\frac{1}{2}\) được gọi là bằng nhau vì chúng có giá trị bằng nhau sau khi được rút gọn: \(\frac{2}{4}\) = \(\frac{1}{2}\).
Để kiểm tra hai phân số có bằng nhau hay không, ta có thể đưa chúng về cùng mẫu số trước đó rút gọn chúng về dạng tối giản để so sánh.
Ví dụ:
Để kiểm tra xem \(\frac{3}{4}\) và \(\frac{6}{8}\) có bằng nhau hay không, ta có thể đưa chúng về cùng mẫu số bằng cách nhân cả tử và mẫu của phân số đầu tiên với 2, ta được \(\frac{6}{8}\).
Sau đó, ta rút gọn \(\frac{6}{8}\) về dạng tối giản bằng cách chia cả tử và mẫu cho ước chung lớn nhất của chúng, ta được \(\frac{3}{4}\). Do đó, hai phân số \(\frac{3}{4}\) và \(\frac{6}{8}\) bằng nhau.
Hoặc hai phân số được gọi là bằng nhau khi:
a.d = b.c
Được kí hiệu như sau:
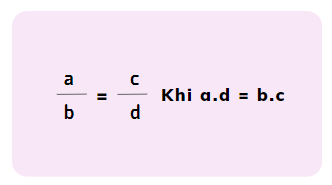
Ví dụ:
Hai phân số \(\frac{1}{6}\) và \(\frac{2}{12}\) có bằng nhau không?
Ta thực hiện so sánh như sau: 1 × 12 = 6 × 2
Vậy hai phân số \(\frac{1}{6}\) và \(\frac{2}{12}\) bằng nhau.
