Tính toán vói số thập phân
Số thập phân là một phần quan trọng trong toán học và được sử dụng trong nhiều lĩnh vực khác nhau, từ các thuật toán máy tính đến các ứng dụng trong khoa học và kỹ thuật. Để hiểu và sử dụng hiệu quả các số thập phân, chúng ta cần nắm vững các phép tính cơ bản, bao gồm cộng, trừ, nhân và chia. Tuy nhiên, tính toán với số thập phân có thể gặp phải một số thách thức, chẳng hạn như làm tròn số hoặc xử lý sai số. Trong bài viết này, chúng ta sẽ tìm hiểu về các phép tính cơ bản với số thập phân và cách sử dụng chúng để giải quyết các bài toán liên quan.
Phép cộng, trừ số thập phân
Phép cộng số thập phân
Phép cộng là phép tính cơ bản trong toán học, và cũng được sử dụng để tính toán với các số thập phân. Để thực hiện phép cộng với các số thập phân, chúng ta cần chỉnh lại vị trí của các số thập phân để chúng đứng ở cùng một hàng với nhau. Sau đó, ta có thể thực hiện phép cộng bình thường như với các số nguyên.
Ví dụ:
để tính tổng của hai số thập phân 2,5 và 3,75, chúng ta thực hiện các bước sau:
- Đưa các số thập phân về cùng một hàng bằng cách thêm số 0 vào phần thập phân của số nhỏ hơn:

- Thực hiện phép cộng bình thường từ phải sang trái:

Vậy tổng của hai số thập phân 2,5 và 3,75 là 6,25.
Lưu ý rằng khi thực hiện phép cộng với các số thập phân, chúng ta cần chú ý đến số lượng chữ số thập phân của kết quả. Để làm cho kết quả chính xác hơn, chúng ta có thể làm tròn hoặc cắt số thập phân theo một quy tắc nhất định.
Phép trừ số thập phân
Phép trừ là phép tính cơ bản trong toán học, và cũng được sử dụng để tính toán với các số thập phân. Để thực hiện phép trừ với các số thập phân, chúng ta cần chỉnh lại vị trí của các số thập phân để chúng đứng ở cùng một hàng với nhau. Sau đó, ta có thể thực hiện phép trừ bình thường như với các số nguyên.
Ví dụ, để tính hiệu của hai số thập phân 5,75 và 2,5, chúng ta thực hiện các bước sau:
-
Đưa các số thập phân về cùng một hàng bằng cách thêm số 0 vào phần thập phân của số nhỏ hơn:
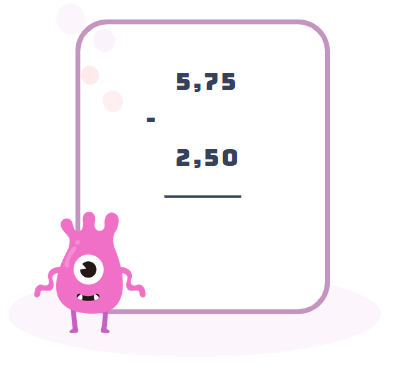
- Thực hiện phép trừ bình thường từ phải sang trái:
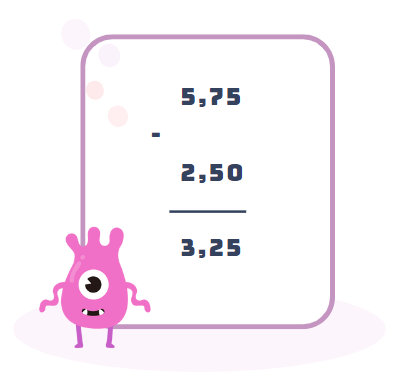
Vậy hiệu của hai số thập phân 5,75 và 2,5 là 3,25.
Lưu ý rằng khi thực hiện phép trừ với các số thập phân, chúng ta cũng cần chú ý đến số lượng chữ số thập phân của kết quả. Để làm cho kết quả chính xác hơn, chúng ta có thể làm tròn hoặc cắt số thập phân theo một quy tắc nhất định.
Phép nhân, chia số thập phân
Phép nhân số thập phân
Phép nhân là một phép tính cơ bản trong toán học, và cũng được sử dụng để tính toán với các số thập phân. Để thực hiện phép nhân với các số thập phân, chúng ta có thể làm theo các bước sau:
-
Đặt dấu phảy thẳng hàng. Nhân hai số như thường lệ
-
Đếm số chữ số thập phân của cả hai số
-
Tính tổng số chữ số thập phân của hai số và đưa dấu thập phân vào vị trí tương ứng trong kết quả.
-
Nếu cần, ta có thể làm tròn hoặc cắt số thập phân theo một quy tắc nhất định.
Ví dụ, để tính tích của hai số thập phân 1,25 và 3,8, chúng ta thực hiện các bước sau:
- Đặt tính rồi nhân hai số như thường lệ:
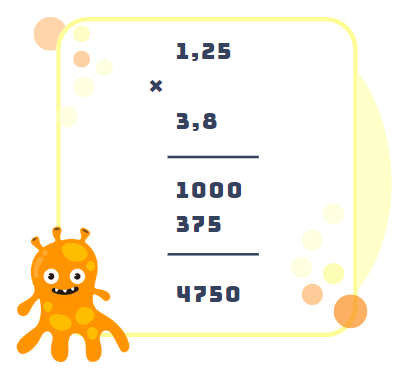
- Đếm số chữ số thập phân của cả hai số, có 2 chữ số thập phân cho số 1,25 và 1 chữ số thập phân cho số 3,8.
- Tính tổng số chữ số thập phân của hai số, là 3 chữ số thập phân. Đưa dấu thập phân vào vị trí thích hợp trong kết quả:
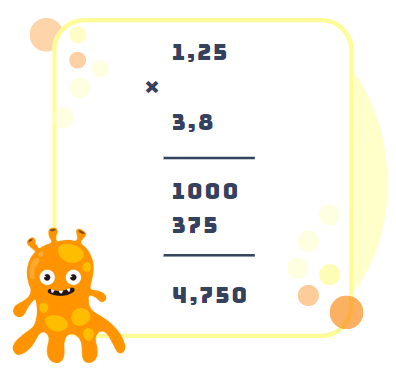
Vậy tích của hai số thập phân 1,25 và 3,8 là 4,750
Lưu ý:
Khi thực hiện phép nhân với các số thập phân, chúng ta cần chú ý đến số lượng chữ số thập phân của kết quả để đảm bảo tính chính xác.
Nếu kết quả có phần số thập phân cuối cùng là số 0 ta có thể không ghi. Ví dụ: 4,750 chỉ cần viết thành 4,75.
Phép chia số thập phân
Muốn chia hai số thập phân dương có nhiều chữ số thập phân, ta làm như sau:
- Đếm xem có bao nhiêu chữ số ở phần thập phân của số chia thì chuyển dấu phẩy ở số bị chia sang bên phải bấy nhiêu chữ số.
- Khi chuyển dấu phẩy ở số bị chia sang phải mà không đủ chữ số, ta thấy thiếu bao nhiêu chữ số thì thêm vào đó bấy nhiêu chữ số 0.
- Bỏ dấu phẩy ở số chia ta được số nguyên dương
- Thực hiện phép chia như số thập phân cho số tự nhiên
Ví dụ:
Thực hiện phép chia 10,773 : 5,13
- Đếm xem có bao nhiêu chữ số ở phần thập phân của số chia thì chuyển dấu phẩy ở số bị chia sang bên phải bấy nhiêu chữ số.
- Khi chuyển dấu phẩy ở số bị chia sang phải mà không đủ chữ số, ta thấy thiếu bao nhiêu chữ số thì thêm vào đó bấy nhiêu chữ số 0.
- Bỏ dấu phẩy ở số chia ta được số nguyên dương

- Thực hiện phép chia như số thập phân cho số tự nhiên

Vậy kết quả của phép tính 10,773 chia 5,13 là 2,1.
Bài tập
Bài 1: Thực hiện các phép tính
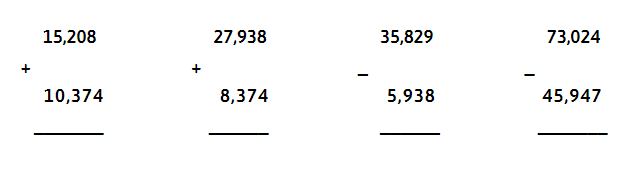
Bài 2: Tính
a) 4,762 × 1,23
b) 83,092 × 5,738
c) 6,039 × 10,018
d) 7,103 × 2,948
e) 6,264 : 1,74
f) 50,7395 : 5,45
g) 14,64 : 4,8
h) 60,75 : 7,5
Đáp án:
Bài 1: Thực hiện các phép tính
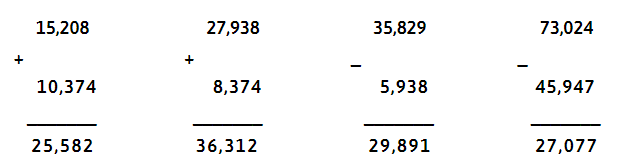
Bài 2: Tính
a) 4,762 × 1,23 = 5,85726 (hoặc bằng 5,9)
b) 83,092 × 5,738 = 476,781896 (hoặc bằng 476,8)
c) 6,039 × 10,018 = 60,498702 (hoặc bằng 60,5)
d) 7,103 × 2,948 = 20,939644 (hoặc bằng 20,9)
e) 6,264 : 1,74 = 3,6
f) 50,7395 : 5,45 = 9,31
g) 14,64 : 4,8 = 3,05
h) 60,75 : 7,5 = 8,1
